背理法不要論ってどうなん？ YouTube動画>1本 ->画像>19枚

東京理科大の先生頑張ってるけど

背理法は不要であると仮定しよう

天動説と地動説みたいなもの
どちらも正しい場合は、簡潔で理解しやすい方が選ばれる

実用品の計算機だと有限の立場が普通だけど

有限の立場は背理法を拒否しません

自己解決しました

まだこれやってたのか

背理法で証明ができること自体は正しいが、どこが誤りであるかを正確に把握しなければならない

背理法なしで数学を組み立ててみればいい
たしか解析で行き詰まる

>>9
背理法で証明できる命題は直接証明可能という定理がある
まあ存在定理だけどな

神は不在である

この話、よくわからないのだけど
例えばその背理法不要先生による
「√2は無理数である」
の証明はどういう形式をとるの？

背理法無用論信者による
「√２は無理数」の証明


任意の自然数 a,b につき、
２ * a * a
　素因数２の個数が奇数
b * b
　素因数２の個数が偶数

よって
２ * a * a ≠ b * b

両辺の平方根を取り
√２ * a ≠ b

√２≠ b / a


のように背理法の逆で証明を進める。

それは背理法を使っていないのではなく、見かけを変えただけ
普通は最後に一度だけ「矛盾するので仮定は偽であった」と書くところを、推論の各ステップで何度も背理法を使っている
各ステップで使われる背理法の矛盾箇所は極めて単純なものなので、「矛盾するので仮定は偽であった」という文言を排しても読者に伝わる
そのため見かけ上では背理法を使っていないことになる

訂正

各ステップで使われる背理法の論証は極めて単純なので
「○○と仮定する……すると矛盾するので○○ではないことがわかる」という書式を省いても読者に伝わる

背理法不要論が実際に背理法を「使ってない」のかどうかはさておき、

「長い背理法は好ましくない」
「矛盾を導くまでの行数をなるべく短くしたい」

という欲求のもとでは、>>13のような証明はアリだろう。

背理法だと偽の命題を仮定することになるから
その下で導出される命題は真でも偽でもあり得てしまう
それが嫌だから(証明の理解にならないから)背理法はダメという話だったと思うので
証明中に偽の命題が出てこない
という点で>>13はアリなのでしょう

>>14
一応途中で間違った命題が入ってないんだから、背理法とは別モノでしょう

>>14
と、いうか各ステップで背理法を使っているというのはどういうこと？使わなくてもできると思うが
もちろん、"使おうと思えば"使えるというだけであって

教科書に載ってる√2が無理数であることの証明は背理法ではないらしい
『Q&A数学基礎論入門』

よくある勘違いで言えば
背理法不要論でいう背理法は数理論理学でいう背理法云々とは別物、証明法の話（主張そのものを見れば明らかなことだけど）
排中律とかはもちろん認めていて
前提に結論の否定を持ってきて始める証明法を問題にしているはず

そういうこと
証明法と言わずに書式の問題だと言った方が分かりやすい

>>13 の証明方法
ネット上でも叩かれまくり

　＝でなく≠で式を変形していくのは、より危険が大きい
　素因数分解の一意性を使用しているが、背理法無用論で証明できるのか？
　分かりやすくなるというメリットが無い。これでは背理法を使った方がより分かりやすい。

などなど

カントールの対角線論法も背理法でしょう。
だから背理法を否定したら、実数の無限集合が可付番集合でないことさえ
証明できなかった訳で。数学は背理法的な逆から矛盾を導くツールが多いよ

>>24
√2の無理数性の証明と対角線論法は背理法といっても違うらしい

>>24
それの直接証明もあったような

>>13
こういうスタイル俺もやるわ。
背理法って要は対偶論法なんだよな。真であることがわかってる命題Aに対して「¬P⇒...⇒¬A」を示して、
そこから対偶で全部ひっくり返して「A⇒...⇒P」とやってPを証明する。
細かいことを言えば頭に量化子がついたりするんだけど、言いたいことは分かると思う。

>>27
背理法と対偶は違う

背理法と対偶は命題論理の公理として互換性があるので、その意味で同じ

アナクロスレ

>>28
わりぃ、根拠書かないやつは一律に無視してるんだわ

>>23
論点を勘違いした人が叩いてるだけ

そんなことはないな
>>23 の論点は重要

これじゃあ背理法を使うべきだな

明らかに「背理法」が変な証明もあるのでそれは排除した方がよい。
例えばある集合からそれの冪集合への全射がないことを示すのに、
「全射があったと仮定する」と言いながら、全射であるという条件を使わず、
単に写像であるということだけから値域に入らないものを作ってる。
それで「背理法の仮定に反する」という証明。変だよな。
普通に、「集合から冪集合への写像は全射ではない」と言えばいいだけだから。

>>35
そういうのまれにあるよな

≠での変形でも背理法よりかは直感的だと思うが

初等的な数学までしか修めていない人は勘違いしがちだが、論理変形だけに目が行って本質を捉え損ねると高度な数学はできないよ
正しさだけを追い求めればいいというものではない
もちろん間違いはないように進める必要はあるが
≠での変形でも、正しさを論理的に確かめてあれば問題はないだろう
どのような手法に基づこうが命題の正しさ自体が保証されることは否定していないし、そこは問題にしていないんじゃないか

命題が論理的に正しいことが理解できるのであれば、その次に重要なのはその命題の証明を含めた理解だよ
ここがおろそかになると真っ当に数学はできない
と、いうよりこの理解度自体が数学における研究に求められる資質の一つ
もちろん、受験数学程度であればそこまで必要はないのかもしれないが
学問として数学を修めるには必要なこと

数学の研究発表においても、
背理法で証明すること自体は問題は無いが
背理法で証明します、なんだかよくわからないけど証明は回ります、というのはやってはいけない
必ず何が本質かということは理解していて、説明できなければならない
だから、背理法を使っていても、何が本質かちゃんと押さえておければいいけれども

例えば学生が重要な命題の証明で何が何だかわからないけど証明だけはできます、という認識だと、理解に重大な影響を及ぼすので教育上よろしくないというのはわかる

とある数学者も言っていたが、物理や化学と違って数学の命題は暗記するものではなく理解する物である
公理さえ定めてしまえば全て道で繋がっている、一つの世界が出来上がるのが素晴らしいところ

そして命題の理解と証明とはとても密接な関係にあるのだから証明のための証明に抵抗を感じる数学者は少なくないだろう

もちろん実践的な研究のうえで背理法が必要になることはあるし、それについては否定していないのでは
あくまで、数学の本質の理解を妨げる危険性に注意しろ、ということであれば納得できるはなし

その持論は結構なんだけど、長々と書いた動機が
「≠での変形でも背理法よりかは直感的だと思う」
という頼りない感想なのが頂けない
結局何に当てはめてよいのか分からない空論に聞こえる

≠での変形
良くないな

すまん
≠の変形がなんで駄目なのか教えてくれまいか

こいつ理科大の先生じゃね？

そんな偉い先生が降臨されたらすごいな

背理法を使った手続きの方が、むしろ数学的(論理的)に見えるけどね。
統計検定などでもそうでしょう。いきなり、実証したい仮説を持ってくるのでなく、
まずは無に帰したい方の帰無仮説を用意する。それにp値などのパラメータを
付与して、その帰無仮説の蓋然性を確率的に検討する。そして、その仮説が
なかなか有り得そうにないと判るとそれは棄却されて、検定者が本来、採用したかった
方の仮説である対立仮説が、そこでようやく採択される。

もちろん、それは確率論的な話なので、ここで採用られた仮説が完全に真である保証は
なく擬陽性や偽陰性の可能性も少しは残る。ただ、ここで言いたいのはそのことでなく、
背理法のような一見すると迂遠で冗長なアプローチにこそ、数学的な真理へ至る本質
があるのではなかろうかという私なりの推論ね。

>>46
本題から外れるから詳しく言わないけど、仮説検定は哲学的に批判があるよ。
エリオット・ソーバーの『科学と証拠』とかに書いてある。

二重否定の除去

>>43
≠を用いることは論理的には何も問題ないのだが、
a≠bからはaがbでないことはわかるがaの構造について何もわからないので、証明はできても理解に繋がりにくい
というようなことが丁寧に38から40に述べられている

個人的には、＝で結ばれるのが一つであるのに対し≠では無数のものが結ばれ得るので考えなければならない対象が多くなるのも問題
多くのものについて議論すると書き手や読み手にとって量的に大変なだけでなく、場合分け漏れがないかも考えねばならないので負担が増える
例えば13の議論は既に23指摘されているように素因数分解の一意性を証明せねばならない、といった具合

>>49
数学は論理だけではできないよ、研究してる体系の本質を理解しないと
直感的な理解が大切
もちろん命題の正しさの保証や計算を回したりする段階では論理が使われるが
それは出来上がったものを使ったり予想の検証をするときに必要になるのであって
直感的な理解をしていないとそもそもそういった数学体系自体が出来上がらない
すでに確立された手法を用いる応用家にはむしろその論理や正しい使い方の面だけでいいけれども、学問としての数学は論理だけでは進まない
そこまでわかって、直感的な理解と証明の本質の理解と合わせてあくまで証明のプロセスの簡略化として背理法を用いるなら問題ない

間違えた
>>50は>>46あて

>>49
前半については曲解

最後の行については素因数分解の一意性については普遍的な性質であり独立な命題なので、数学を体系的に理解していく上で問題はないと思う


要するに論点が違うんだと思うが
背理法を使うのに気をつけろと言ってる人は本質の理解を重視していて
このスレでの批判的な人は証明としての簡略化を重視している

背理法では証明は正しく回っても「なぜ成り立つのか」を本質的に見落とす可能性があるし、途中で出てきた命題は基本的に成り立たない
直感的な証明においては証明の途中においては正しい普遍的な性質が得られているので、なぜそうなっているのかが分かる

>>50>>52
なるほど、そういう考え方があるのですね。それって、位相幾何学者の
ブラウワーなどが提唱した背理法や推論規則を捨象する「数学的直観主義」みたいな
立ち位置なのでしょうか？

ただいくら直観的な証明が得られても、やはりそれが真か偽かを論理的に証明してみないと、
そこに誤謬のリスクがあるのではないか。たとえば、古代人にとっての直観は、地球は平面で
あり、かつ、プトレマイオス的な天動説を皆で信じていた。コペルニクスの地動説が
出てくるまでは。だから、直観を使うから対象の本質や普遍に迫れるとは限らないのでは？

むしろ人間の認知の特徴にあるのはバイアスや偏差、歪曲化、恣意性、忖度であるので、
そこを超える為に論理が要請される気がする。

哲学者のヒュームは、論理をもっと先鋭化させるか、あるいは科学的な論理性や
真実性をも懐疑にさらす。たとえば、ヒュームは太陽が東から昇り、西へ沈むことは
必ずしも客観的な事象ではないとする。それは、ただの慣習的に見られた認知に過ぎず、
明日も未来もまた必ずそうだとは言えない、といった考えを述べた。

一見すると荒唐無稽なこのヒュームの主張こそが、実は真に論理的なものであると
言える。なぜならこの宇宙空間や地球環境に著しい変異が生じたりした場合には、
既存の科学体系がそのまま適用出来なくなる可能世界も十分に考えられるからだ。
それは非ユークリッド幾何学の世界では、ユークリッド幾何学の価値観だけでは
不十分であるのと同じこと。だから、論理性もそれを先鋭化させていくと、
チューリングマシンのような単なる機械的な自動手続きを超えた真理みたいなものが
垣間見えるかもしれないよ。

＞最後の行については素因数分解の一意性については普遍的な性質であり独立な命題なので、数学を体系的に理解していく上で問題はないと思う

これ数学の否定

>>52
＞素因数分解の一意性については普遍的な性質であり独立な命題なので、数学を体系的に理解していく上で問題はないと思う
数学に対しその程度の認識でよくもまあ本質だの一つの世界だの理解だのと宣えたものだ
ツェルメロやフレンケルやヒルベルトといった先人を侮辱しているとしか思えない

>>55
>>56
おおかた啓蒙書の内容垂れ流してた中学生がボロ出したってとこだろ
可哀想だからほっとけ

>>53
直観主義までは行き過ぎというか、排中立を認めない数学者はほとんどいないと思う
少なくとも解析、代数、幾何系では


>ただいくら直観的な証明が得られても、やはりそれが真か偽かを論理的に証明してみないと、そこに誤謬のリスクがあるのではないか。

これはもちろんその通りで、論理的に正しいことの証明は必須、前提ではある
論理的に正しいことを確かめたうえで、なぜそうなっているのかの理解が大切ということ
もちろん殆どの数学者は背理法を使っていもそれができているし、取りこぼすことはない
ただ、学生とかがそうならないように気をつけようね、という意味で配慮している先生とかはいる

>>56
すまんがなにをいってるかわからない

>>57
かわいそう
なにか数学にコンプレックスがあるんだね
一方的に見下すことしかできないなんて
かわいそう

ちなみに私の専門は幾何系で、基礎論とか論理学の深い話はそこまでできないよ
あくまで代数とか幾何とか解析のくくりの数学者のコミュニティや共通認識がある程度わかるだけで

>>53
ちょっとだけ加えていうと、確かに直感だけでは取りこぼすような所もある
式の上での変形でしか進められないようなものもあるし、直感的な理解がほとんど得られないが証明はでき有用な命題や補題というのもある
そういった意味では、直感によらない論理的な操作がなくてはならない部分、というのは存在していたのだと思う
しかしながら、少なくとも私がこれまで学んできた数学の理論（最新の研究分野も含む）においては、そういった例外は少数であり（もちろん重要なものではあるが）、基本的には各分野は直感的な理解やなんらかの意味付けをもとに体系化が進められていくものであると断言できる
仮によくわからない性質があったとしても、それをそのまま鵜呑みにせず新しくいろんな概念や体系を作り出すことでそこになんらかの意味を見いだそうとする試みが現代までの数学を形作っていると言っても過言ではない
もちろん直感だけでは理解出来ない命題が現れたときに直感によらずある程度証明できるような力は必要だと思うがね




まあ直感ということを強調しすぎたけれども、ざっくりまとめると
論理に基づいてしっかりやることも、直感的に理解することもどちらも大切だということ
数学に慣れてる数学者が背理法を使うことにはなんら問題はないが
あまり慣れてない学生は背理法だけで証明を回して、命題の成り立つ本質を見失ったりしないように気をつけよう、教える側もそうならないよう注意しよう
ということだね

イメージとしては
論理的な力は、足場を固めるための力
直感的な理解は、その体系の本質を理解するため、先へ進めるための力

>>54
中々興味深い話ではある
先に述べた通り、私のわかる範囲（いわゆる解析学や代数学や幾何学といった分野）の理論は必ず何らかの性質や概念を体系化していくものなので、論理だけでは必要な定義もわからず、体系として形作ることもできない

しかしながら、人間的な要素を排除して、論理を論理だけで繋げていった先に何があるのかは面白い話だと思う
それについてはどうなるか楽しみにはしている

明日も同じ繰り返しだと発狂するほど退屈ですか？

言っちゃ悪いけど、宗教者の戯言と同じだね、理屈の類ではない
都合よく「これは神の御業だ、神の試練だ」とか定めて世界観つくってるアレ
信じる者にしか通用しない

その教義における
「背理法を使わない方がわかりやすい」
という点がまるで信じられない

素因数分解の一意性
って本当に背理法じゃないと証明できないの？

んなこたーない
排中律がなくてもm＜n∨m＝n∨m＞nは証明できる
後はお馴染みの素因数分解の一意性証明でよい
m＜nとm＞nのときは矛盾するのでm＝nと分かる

矛盾て

世界はそれを背理法と呼ぶんだぜ

直観主義論理で証明できるかといえば、できる
m＜nとm＞nのとき矛盾を導くのは、背理法のプロセスではなく、m＜nとm＞nの否定に過ぎない
表面上、背理法の形式をとるかどうかを問題とするなら、既に指摘されたように背理法を対偶に書き換えることで解決済み

そっからどうやってm=nが出てくるんですか？

命題
無理数⇨既約分数で表せない

対偶
既約分数で表せる⇨有理数

背理法で証明できたと思っても計算ミスだったということは起こりがち

≠で式を変形するよりはまし

背理法不要論はよく分からんけどそれと同じくらい
≠変形よくない論も分からない

胴上げして突き落とす論法

背理法がどうこうじゃ無くて、

数学において
数学において
数学において

1. 証明とは公理から推論出来ると言う意味であり、
2. それ以外の意味は全く無い、

この二つを認めるなら、数学において背理法が正当なものであることは全く明らかであり、認め無いなら数学を理解し行うことは不可能だと言うだけのことだ。
多分数学における背理法の有効性を疑うヤツは、演繹と帰納の区別すら出来てないただのアホだろ。
でなきゃシュレーディンガーの猫ガーとかの、単に混乱を望んでいるだけのキチガイか。

背理法とは、結局否定出来ないことを示すと言うことだ。
公理から推論出来ないとしたら辻褄が合わないのだから、公理から推論出来るのだと言うだけのこと。

小学校のとき面積を出すのに引いて出した問題があっただろ。そのほうが計算が簡単だったから。
そんなんと結局同じことだよ。

＞背理法とは、結局否定出来ないことを示すと言うことだ。
＞公理から推論出来ないとしたら辻褄が合わないのだから、公理から推論出来るのだと言うだけのこと。

全然違う

>>80
お前がね。

背理法と言うものを何か特殊なもののように思っているから理解出来ないだけだ。
我々は普通に日常でも背理法を使う。
「～～だとしたら、、、、いやいやそれじゃ～～が～～したことになる。そりゃいくらなんでもおかしい。あり得ん。やっぱり～～のはずだ。」
こういう考えかたは誰でもやるだろう。
これは背理法だ。

二人とも「推論できない」と「否定が証明できる」を混同している

対偶証明法と背理法って違う方法だよね

あと背理法が構成的でない云々の指摘についても、一見正しそうで的外れだ。
数学の第一義は厳密な証明にある。
「代数方程式は複素数の範囲で必ず根を持つ。」代数学の基本定理だ。
根を求める方法について、全く構成的でない。
では代数学の基本定理は無意味なのか？
「微分と積分は逆演算だ。」解析学の基本定理だ。
しかし積分や微分を求める方法について何も語って居ない。
ではこの解析学の基本定理は無意味なのか？


　

二人とも、じゃないな
同一人物か

>>83
バカはお黙り。

>>83
「公理から推論出来無いことが証明される。」
「否定が証明される。」
同じだアホｗ

事実：（ZFCが無矛盾ならば）連続体仮説はZFCから推論できない
誤解：（ZFCが無矛盾ならば）連続体仮説の否定がZFCで証明できる

>>89
（ZFCが無矛盾ならば）連続体仮説はZFCから推論できないことが証明される

（ZFCが無矛盾ならば）連続体仮説はZFCから推論できないのは誤りであるとすることの否定が証明される

全く同じですなｗ

>>89
連続体仮説はそもそも連続体仮説をZFCと独立な公理とすべきかどうかと言う問いだろう。
公理を固定して話しをしている場合とは違うだろが。

処置なしだな

お前とかなｗ

ロジックの基本さえ知らないなら公理とか推論とか言わなきゃいいのに
馬の耳に念仏とはこのことだな
自分の使ってる言葉の意味さえ知らない者には処置なしだ

横レスだが。。

公理系を ZFC に固定する。ID:EOqQyi8Y によれば、ZFC の中で記述できるいかなる問題 Q も、

「 Q が ZFC から推論できないことと、￢Q が ZFC で証明できることは同じことだ 」

と言っていることになる。たとえば、Q として

Q： √2 は無理数である

という問題を考えてみると、Q は ZFC から推論できないし、￢Q は ZFC で証明できる。

……ということでいいのか？

すまん、Q の中身が逆だった。たとえば、Q として

Q： √2 は有理数である

という問題を考えてみると、Q は ZFC から推論できないし、￢Q は ZFC で証明できる。

……ということでいいのか？

そのQは反例にならない
反例になるのは次のどちらかの場合
・Qは証明できないし、Qの否定も証明できない
・Qは証明できるし、Qの否定も証明できる

前者ならQは独立命題と呼ばれる
後者なら理論は矛盾している

>>97
いや、この Q 自体が反例になっている必要は無いんだ。
あくまでも ID:EOqQyi8Y がこの Q のことをどう思ってるのか知りたかった。
あるいは

Q1： RからNへの単射が存在する

とかでもいい。Q1 は ZFC から推論できないし、￢Q2 は ZFC で証明できる。
だから、この Q1 も反例にはならないんだが、反例になっている必要はなくて、
ID:EOqQyi8Y がこの Q1 のことをどう思ってるのかなっていう。

またミスってる。Q2じゃなくてQ1だ。。

× Q1 は ZFC から推論できないし、￢Q2 は ZFC で証明できる。
〇 Q1 は ZFC から推論できないし、￢Q1 は ZFC で証明できる。

もし数学に背理法を不要とした場合、どうなるかを背理法で証明してみよう


数学に背理法は不要である(命題)

背理法を使わない数学体系は、夥しい困難と混乱、カオス、狂気に陥った

よって、数学に背理法は不要であるという命題は、数学の成立と整合性と矛盾する

すなわち背理法によって、数学における背理法の必要性が証明された(証明終)



これはトートロジー(恒真命題)ですｗ

>>78
論点がずれてると思うんだけど
論理としての正しさではなく、直感的な意味を理解するための方法論として議論されていると思うのだけど
君はまず数学をやる前にまず日本語の復習からだな

例えばチャーハンを作るときに

「初めに卵とご飯を混ぜておくとパラパラになりますよ」
という意見に
「後から卵をいれてもチャーハンはできるだろう！？何を言ってるんだ」
と反論してるようなおかしさ

数学を語ろうという人間が論理的に話をできないのは恥ずかしいことだと自覚して欲しい

>>85
これについても、厳密な証明は前提条件だということをわかっていない

もうちょっといい例えを思いついたが
プログラムなんかで、ここはifelseよりforを使ったほうが見やすいとか、forより～を使ったほうがわかりやすいとかあると思うが、そういった話でしかない

それに対して、ifでもちゃんと回るんだ、とか、同じ条件を表してるんだ、とか言っても仕方ないだろ

そもそも教育上の話ですし
>>100の証明もどきは意味不明ですし

>>105
それ戯れに書いただけなので、素で受け取らないでくださいｗ

ただ、数学のテキストを見ると、証明で背理法が使われているのを見ることが多いので、
もし、背理法が不要となったら、世に出回っている数学のテクストが大幅な修正や改訂を
余儀なくされて、困るだろうなという感想を持ちました。

それに、もし、背理法がない方が数学の利便性なり、見通しが良くなる、または数学の本質に
迫りやすくなるということであれば、古の天才数学者、たとえばガウスやオイラー、カントール
などがそうした背理法不要論の考えを少しでも述べていたはずで、それらがないということは、
数学において背理法は必須の道具や要素である、というのが推論できるということです。

藤林丈司

このスレの結論！

背理法不要論は不要でした

はあ？

>>1

矛盾の証明には背理法が必要となる。

>背理法不要論は不要でした

良い結論が出ました

これが"背理法不要論不要論"の始まりである。

誰も論じないので終了に

背理法の歌
ハイリハイリフレハイリホー

大きくなれよ

>>3
天動説は正しくない

背理法による証明は危険ではある。
1つの間違った命題からすべての命題が導かれてしまう。
普通数学者は自分が使う定理の証明を全てフォローしているわけではない。

>>117 がバカであることが証明された

>>118
正しくない命題を「証明した」論文は珍しくない。
念のため言っておくが、「結果は正しいが論証が間違っている」のではなく、結果自体が間違っている論文。

それが背理法と何の関係があるん？

ある命題を証明するとき「それが偽だとすると、誰々が示した結果に矛盾するから背理法によりこの命題は正しい。」という論法は普通に使われるでしょ？

「誰々が示した結果」の真偽の話ですか？

背理法全く関係ないｗ

関係あるじゃん
研究で使う道具だてを全部厳密に証明チェックしてるわけじゃないんだから

>>124
え、お前チェックしてないの？

はあ？

背理法でなくても「誰々が示した結果」を引用するとき常につきまとう問題でしょそれは

数学じゃあダメ
引用した文献が間違ってたら、引用者にも責任及ぶ

たとえばπが超越数であることを多くの人は知識として知ってるだけで、実際の証明をフォローした人は数学者でも半分もいないだろう。
しかし円積問題を解いたという論文が有ったらインチキ扱いをする。
このとき暗黙のうちに背理法を使っている。

それのどこで背理法を使ってるの？

少なくとも超越数の論文を書く人はきちんと実際の証明を理解する必要がある

>>129
証明に基づかずに主張するやつは数学者じゃねえから
ただの大学職員

江戸末期の田舎の下級武士に経済ユダヤが支援してテロを起こさせ江戸幕府を転覆させたのが明治維新。
江戸末期から日本は経済ユダヤとの繋がりがありお互いの利益の均衡を目指してきたのが今日までの政治
の中心課題だと言えます。複式簿記　資本主義　株式制度 現在の経済の根幹を作ったのは彼等であり、
全ての産業を掌握する彼等（総資産数京円以上）の意向を無視出来ません。旧ソ連　中国共産党　北朝鮮　
ISISを作ったのは彼等であり、日本の技術流出　東芝の半導体事業からの撤退、シャープの倒産全て彼らの
シナリオ通りに動いてます。また、ここ数百年における世界の全ての紛争、戦争は彼等によって引き起こさ
れました。
彼らの目指している世界は自分達を支配階級とした人類の管理であり歯向かう人間の排除です。　
私達が右や左と罵り合う姿は彼らにとって好都合であり、対立は彼らの支配体制の強化になります。そういっ
たことを全ての日本人が理解しないと同じことを繰り返し、十数年後　あの時安部が日本を滅茶苦茶にした。　
今度の保守の誰々さんこそ日本を救うと喚いてるかもしれません。消費税廃止　移民反対と当たり前のことを
各政治家に要求し続けると同時に政治家は全員ユダヤの手先だと疑い続けないと日本の独立は成し得ません。

世界中の人間が知るべきこと

・世界の全てのメディアはユダ金が牛耳っている。

・トランプ　プーチン　習近平　安部　麻生　テリーザ・メイ　メルケル　文在寅　金正恩はユダ金の手下であり仲間である。
テレビに出てる有名な政治家は国内外問わず全員ユダヤの手先だと考える事。右や左などによる対立は茶番である。

・全てのテロと紛争と戦争は、ユダ金達と軍産複合体によって引き起こされている。

>>132
ヴォエヴォドスキの論文の定理が間違っていて他の数学者は間違いに気付かず引用していた、って話聞いたことない？

間違いに気付かず引用したことで非難されたんだろ

やっぱり背理法は関係ないじゃん

>>134
"引用"ってのがそれを正しいこととして主張することを含むなら、そいつら全員数学者じゃねえ
証明を飛ばすって数学者がやっちゃいけないことだからな

その"引用"が「もしこれが正しいならば、・・・が言える」っていうふうに条件文の前件に持ってきてるだけならもちろんセーフ

「ナントカ予想」の引用は良くある

規範と自然法則を混同してるヤバい人がいるな
「○○しちゃいけない」が「○○なんてあるはずない」にすり替わる

だから「…とすると○○であることに矛盾する」という論法は○○が長年に渡って確証された命題にしか使えない。

○○が正しければ問題ないということですよね

例えば上に出てきた「素因数分解の一意性」だって、Ｚ[1の原始n乗根]でも成り立つと無根拠に思い込まれていて、
フェルマーの定理を素因数分解の一意性を使って背理法で解こうとする試みがあった。

>>142
>とする試みがあった
あったからって何だよw

>>143
知らない？コーシーのような大数学者がこのアプローチで解こうとした。
n=3,4のときはそれでうまくいくからね。

数学者じゃないと指摘されて動揺したから19世紀までさかのぼって自分と同じことしてるやつ探してるの可愛いね

>>145
マジで意味不明
現在だって起こり得る話なのに

だから背理法の話じゃないですよね？

>>130
πが超越数でないとすると、πは代数的数で、πの有理係数の最小多項式が存在する。
超越数の証明における背理法の議論では、基本的にこのことを念頭において上手に矛盾を導く。
証明方には、オイラ－の公式を用いる方法や、他の方法もある。
πより前に超越性が示されたeでも有理係数の最小多項式の存在性を仮定する点では同じ。
こちらでは、多項式関数や積分を設定して上手に矛盾を導く。
代数的無理数やeの無理数度は2だから、eの超越性の証明にはディオファンタス近似は使えないだろう。

「論文を書け」っていう圧力が強くて証明を読む時間がないんだろうけど、読まないことが正当化されるわけじゃないからな？

真か偽か自分で分かってないことを真だと主張するようなのは数学やってるって言わねえから

>>130
>>148について
証明方 → 証明法
オイラ－の公式 → オイラ－の等式

>>149
証明はダメもとでも一度自分で試みてみるモノだ。
そうした方が、得られることは大きい。

素因数分解の一意性が全ての代数体に当てはまるのではないことは、
今の教科書ではきちんと注意言及されている事

１は素数ですか？

ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ

１が素数でないのは、そのように定義しているから。

>>152
それは今では常識ということでコーシー当時はそうではない。

コーシーをいじめるのはやめろぉ！

連続関数は少なくとも一点で微分可能であると信じられていた時代もあるよぬ

5=1・5=1・1・5=1・1・1・5=

ｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ

>>1
ただのトンデモですな。

ここでの議論が意味があり、背理法にも欠陥があるとしても
それが理科大のセンセが正しいという結論に直接は結び付かないという当たり前の論理をここに記しておく

>>12
多項式x^2-2はアイゼンシュタインの既約判定法より有理数体上既約
根pの最小多項式の次数が1であることとp∈Qであることは同値
よって√2は有理数ではなく無理数

そのアイゼンシュタインの既約判定法を、背理法なしで証明する必要があるな

トロトロ証明を読んでて論文が書けないからって、証明を読み飛ばして論文量産してるやつに噛みつくのやめろよ

背理法は対偶証明法の一種か対偶証明法が背理法の一種か
明快に教えてエロい人

>>164
形式的にはどっちを仮定してももう一方が出る

哲学的には、背理法は大域的な手法で、論理体系全体の無矛盾性を根拠にしてる
無矛盾性を仮定していい場合には使えるけどそうじゃない場合には使えない
対偶法は局所的な手法で、P→Qと￢Q→￢Pが同値であるようなP、Qのペアがいくつか既知なら
それらを組み合わせて成立する。論理体系全体の無矛盾性については考えなくていい

>>164
狭義には違うもの
ウカシェヴィチの公理系では「対偶による証明」、
つまり「¬p→¬qからq→pを推論する」ことはできるが、
「狭義の背理法による証明」は「排中律(公理)」かまたは「二重否定の除去(推論規則)」がないとできない(ウカシェヴィチの公理系では二重否定の導入はあるが上の2つはない)

らしいです
間違ってたらごめんな

＞論理体系全体の無矛盾性を根拠にしてる
してません
矛盾していれば何でも証明できるのだから背理法の証明だって常に成り立ちます

>>165
注釈だけど一行目は古典論理みたいな無矛盾律かその仲間を仮定した体系を暗に仮定してるから
後半部分と問題意識がずれてる。

>>167
体系が矛盾してることを知りながら、あるいは矛盾してるかもしれない体系に対して
背理法を公理として導入することが科学哲学的に不正だってことは分かる？

あなたは全知全能の神ですか

議論のやり方が分からないやつが数学板に来るなよ　笑

喧嘩すんなポテトども

全知全能の神です

０＝１

とすることに決定しました。

>>173
驚きを持って確認すると
0!=1!
ということ？

飛躍しすぎだね

0^0 = 1^1

でいいでしょう

ＡＡみたい
(0^0) = (1^1)

CCLemon
((0^0) = (1^1) )♡

哲学やると全知全能の神になっちゃうんだなあ…

お馬鹿さんのために解説してあげます
全知全能ではない普通の人にとっては、あらゆる体系が「矛盾してるかもしれない体系」なんですよ

無矛盾が証明されている公理系もある

体系Tが無矛盾だと証明されている　＝　「Tで矛盾を証明できる」と仮定すると（メタレベルで）矛盾することが（メタレベルで）証明されている

これはTで矛盾を証明できる可能性を否定するものではない

>>181
群論の公理系とか実数体の公理系とか構成的に無矛盾であることが証明されている。

>>182
その証明は、群論や実数論自体の言語を用いて証明されていますか？

あほらし

だから、自己言及のパラドクスなんでしょ。
クレタ人の嘘つきパラドクス。

その島民が全員嘘つきで有名なクレタ人が住むクレタ島。そこから一人のクレタ人が観光客に「わたしは嘘つきです」と言った。この文の言明は、すなわちこの命題は
真なのか偽なのか判らないでしょう。

もし、このクレタ人が本当のことを述べているとしたら、すべてのクレタ人が
嘘つきであるという前提(公理)と矛盾する。また、このクレタ人が嘘を述べて
いる、すなわち、このクレタ人は本当は正直者であるなら、これもまた、
前提であるすべてのクレタ人は嘘つきであるという前提(公理)と矛盾する。

つまり、パラドクスに陥る自己言及は避けなければならない。
その言及システムの外部にいるという前提が必須となる。

たぶん論理についての無理解がある

ラッセルのパラドクスは、論理そのものなんだけど。

ラッセルの逆理、どこが？

まさか、数学板でラッセルの型理論も知らないのではあるまいな。
ホワイトヘッドとの共著「プリンキピア・マテマティカにあるよ

それだけ、いいたいことは？

>>182
そのやり方では、公理系のモデルを構成する側の体系の無矛盾性に問題を移し替えただけ

>>191
やっぱりわかってない
具体的な証明を読んでないだろ

思わせぶりな言葉で周囲のよく分かってない人達を騙そうとするのやめて

>>179
お前マジで1個のりんごと２個のりんごが同じものかもしれないと思ってんの？
爆発律を仮定するなら「矛盾してるかもしれないと思う」ってことはそういうことだから

一言で言えば、現実世界が理論のモデルなんよ

そういうことだ。

解を予想するのと同じ

帰納法から導けるのは仮説のみ(´・ω・`)

論理式の計算に詳しい奴は多いけど、形式理論と現実世界の接続部をちゃんと理解してるやつって少ないよな
そこが科学哲学なんだが

>>1
酎ハイ率だっけ？

背理法って、なんか二重否定の除去とそのロジックが似てない？
命題の否定を否定出来れば、その命題の真理値が真となるは、
結論の否定を用いて矛盾命題であることが示せれば、命題の証明となるのだから、
似ている感じもする。
逆問題だとまた違うだろうけど、それでも裏や反対、逆から考えるという
発想自体は似ていると思うので、背理法は数学らしいアプローチやね。
それと、なんで帰謬法という呼び方はあまりされないのかね

>>201
なんでそんなトリビアルなこと言い出せるかの方が不思議なんですけど・・・

ぽっと出てきてバカなこと言って論破されると消えるやつwwwwwwwwwwwwww

「無矛盾律を否定する者は、打たれることが打たれないことと同じでないと認めるまで打たれ、焼かれることが焼かれないことと同じではないと認めるまで焼かれるべきだ」って言葉を思い出した

で、このスレの結論は？

>>205
お前がビッグバン以来の池沼ということだ

>>206
お、俺？！
ヒエ～～～～

ビッグバン以来なら宇宙が範囲だろうし、褒め言葉にしか思えない

池沼のギネス記録って賞金もらえたりすんのかなw

数学が無矛盾なら背理法使っていいってことじゃん

いいよ

広田良吾が馬鹿でワロタ

>>212
誰？背理法と関係あんの？2015年に死んだって書いてあるけど

間違えた
背理法じゃなくて数学的帰納法は嫌いだと書いてあった
ソリトンの人
広田微分で有名

背理法と言いながら背理法の仮定を実質的には使ってないような証明は排除すべきだとは思う。

でも、背理法でない証明を書こうとするする時、まず背理法を使った証明をしてからそれを元に背理法を使わない証明を作るしかないことってあるんじゃない？

>>21
>数理論理学でいう背理法云々とは別物
数理論理学でいう背理法って何なの？

>>25
なんで？

>>35
>「全射があったと仮定する」と言いながら、全射であるという条件を使わず、
俺の知ってる証明は全射であることを使ってるけど
使わない証明ってどういうのか教えて

>>37
a≠-a
だけど
a^2≠(-a)^2
ではないってことを危険と称してるんだろ思う
あの部分は
(√2*a)^2=2*a*a≠b*b=b^2
だから
√2*a≠b
とするべきだと思うけど
それでもf(x)≠f(y)ならばx≠yってのは背理法使うんじゃないの？

>>88
違うでしょ

>>218
f：A→P(A)を写像とする。
S＝{x∊A：ｘ∉ｆ(ｘ)}
とすればよい。
S∊P(A)だがｆの値域に入ってない。

>>221
続き(自己レス)
この証明でSがｆの値域に入っていないことを示すには普通は背理法を使うだろう。
しかし、「ｆが全射」という強い仮定を使うことはない。

背理法を使うと実際に証明に必要な仮定より強い仮定をしてしまいがちになり証明の本質が見えにくくなるのは事実だと思う。
しかしだからと言って背理法を一切使うなと言うのもどうかなとも思う。

>>222
制限する必要はないな

背理法不要論者の言い分だと0^0は1でしか有り得ないらしい…

ある条件の下で成り立つ命題を証明して、後にその条件を緩めることが可能、というパターンはよくある。

自然数から複素数に至るまで集合で定義できる
ってのと
#φ^#φを満たす集合は唯一つである
ってので
0^0=1
でしか有り得ないっという背理法不要論者の主張

一方で
lim[x→0](x^(log_x(e)))=e
だよね…

0^0の値が何であるかと
x^yが(0,0)で連続でないことは関係ないんでしょ
それ自体は別におかしくないと思うが

0の0乗と背理法がなんの関係があるの？

空写像の認識 0^0=1 : 系 - 背理法被害者の会
http://www.ma.kagu.tus.ac.jp/~abe/sub6.html

>>227
0^0を空集合から空集合への写像の全体と定義するかどうか
(-1)^(-1)とか決められないし
(1/2)^(1/2)もな
べき乗の定義は積までと違って定義する集合によって違う

え？負整数乗や有理数乗もダメ？商集合で整数、有理数、実数、複素数まで構成していけるのに？

[PDF] 同値関係と商集合
http://www.math.sci.osaka-u.ac.jp/~matsumoto/lectures/2016-fs2/docs/2016-fs2-C.pdf

背理法をつかった証明は直接法に機械的になおせるって本当ですか？
コンパクト集合上の連続関数が一様連続である背理法の証明は初頭的だけど直接法はコンパクトの性質をもろに使っていてわかりににくいけどできるのかな？

>>231
それって最初の奴（有限集合間の写像の総数）を拡張してるだけ
拡張の仕方が一意なんてことはないよ
まあ
集合概念を拡張した超現実数なら-1個とか-2個とか有理数個とかできたと思うけど

高添沼田（葛飾区青戸6－２３－２１ハイツニュー青戸103号室）の挑発
高添沼田の親父「関東連合文句があったらいつでも孫を金属バットで殴り殺しに来やがれっ!!　関東連合の糞野郎どもは俺様がぶちのめしてやるぜっ!! 賞金をやるからいつでもかかって来いっ!!糞バエ関東連合どもっ!! 待ってるぜっ!!」 (挑戦状)

まあ実際複素関数として考えたら違ってくるけど、そこは常識的に考えるものだろう

0^0なんていう使わない概念を真面目に考えてもしょうがないだろ。
俺は0^0=1億と定義するわ。文句あるか？

文句ない

0か1以外に定義したら、普通の分配法則さえ成り立たないぞ

>>12
x^2=2が実解を持つなら±2、±1である。√2は解である。よって√2は無理数。

>>1
背理法で証明できる命題が背理法を使わなくても証明できることは正しい。
このことは基礎論の研究者によって、かなり前から証明されているようだ。
ただし証明のルートが二つあるなら、一つ見つけた段階で論文にした方がいい。背理法不要論の先生も、自分の院生が論文を書く場合、
背理法を使うなとは言っていない。背理法が正しい証拠だろう。
背理法が数学的にも論理学的にも正しいことは明らかなのだから、
背理法不要論が意味を持つのは、
背理法が数学教育上悪影響を与えることが実証された場合だけだ。
すなわち、背理法不要論は数学や論理学の問題ではなく、教育の問題だ。
ところが、この部分に関する客観的なデータは皆無だ。
件の先生も自分の主観的な経験を述べているに過ぎない。
この部分について、他者の検証に耐えるデータに基づいて主張しない限り、
科学的でないので誰も相手にしないだろう。そりゃそうだ。
何の興味もない誰かの趣味に付き合う暇人はそうそういない。
今の状態では5chのネタが精一杯だ。5chでもスレオチするかもしれない。

>>240
纏め乙

直観主義

>>240
小保方晴子の「STAPは絶対に存在します!」とのアナロジーがあるということだね

再現性や証明のない自論の固執だけでは、誰も説得できないという、ごく当然の帰結

教育方法に実証や再現性を求めるのはどうなんだ？？？

だがドイツでSTAP細胞の実在が認められ、日本のマスコミの伝え方の劣悪さがまた新たに判明
未だに日本世間ではSTAP細胞の科学的実在性さえ認められていない

>>245
仮に、それが本当でも
小保方が発見した（作製）出来た事の証明にはならない
例えば、私が「宇宙人はいますっ」て言えば、最初に発見された時の栄誉は私のものになるのか？

>>246
俺が言ったのは実在性の是非で氏の功績の是非じゃないから
マスコミの伝え方・記者質問の仕方は
STAP細胞という概念をトンデモ科学概念と見せかねない報道をした
言ってみればiPS細胞をトンデモ扱いしていた人間の所業に等しい

>>247
あんた馬鹿だなぁ
もともと、小保方達が作製したと発表した事が批判されていただろ？
STAP的なもの自体はその前からあるかも知れないと言われていて、それを偽造して発表しただけ
お前みたいな頭の足りん馬鹿がそれを混同してるだけ
どっか行け

>>248
> STAP的なもの自体はその前からあるかも知れないと言われていて、それを偽造して発表しただけ

そのあるかも知れないをトンデモに仕立て上げたのがマスコミ

> お前みたいな頭の足りん馬鹿がそれを混同してるだけ

お前みたいな既存概念依存人間が状況を覚えてないだけ

背理法という証明方法はエレガントな感じがするので、むしろ数学に相応しい気がする。
間接的に真理を求める、といった感じ。直接・直截的なのは、なんか野蛮な感じがしないかい？

>>250
野蛮な感じか、
初めて聞いた、面白い感想です。

野蛮かはともかく非構成的な証明を未だに否定してる人がいたら流石にな

>>245
寝言は寝て言え猿ｗｗ

>>249
寝言は寝て言え猿ｗｗ

問: 無理数の無理数乗が有理数となる事はありえるか？
解答: ありえる.

証明:
α ＝ (√2)^(√2) について考える.
(1) α が有理数だとしたら, √2 が無理数なので α自体がその一例である.
(2) α が無理数だとしたら, α^√2 = 2. これも同様.
どっちにしろありえる事が示された.
( 本当のところ α は有理数なの？無理数なの？ 証明においてその知識は不要である.)

背理法否定論者は、この証明も叩きそうだなあ...

なんでそう思うん？
ただ場合分けしてるだけだよね？

>>254
君は議論では249に負けているよ。

ここは数学板ではなく言い負かせ板

>>255
背理法とどう関係があるの？

直感主義的方法ではないですね

αが結局どちらかなのか述べていませんから、何も言っていないのと同じです
直感主義では排中律は認められません

>>257
寝言は寝て言え猿ｗｗ

>>246
小保方氏が細胞を変化させて、その細胞から若山が幹細胞を作った。
ところがそれは若山研究室のES細胞だったと遺伝子解析で判明した。
検証実験は若山は逃げた。小保方氏は細胞を変化させることには成功した。
マスコミは最後まできちんと報道しただろうか？

今日も背理法を使ったせいで頭が腐った

わざわざ背理法を使わなくてもいいのに使うやつはマゾ

選択公理を使わなくても比較可能定理を使えばいいぢゃん

ゾーンの補題でイイジャン

>>240
>背理法で証明できる命題が背理法を使わなくても証明できることは正しい。
>このことは基礎論の研究者によって、かなり前から証明されているようだ。
ちょっとちがくて
背理法というか
排中律無くても二重否定命題は証明可能（埋め込み定理）
でも二重否定命題から命題を証明するのに排中律（背理法）が必要

背理法＝対偶を証明する
だろう。

丸大ハムの宣伝を聞くと、背理法を思い出してしまう。

最近、妹がグレブナー基底に興味を持ち始めたのだがも背理法不要信者が書いたのか

背理法不要論を振りかざす奴は、丸大ハンバーグを食べるの禁止。
（昭和のCMを知っていればわかってくれるはず。）

>>271　これのこと。

たしかに言いたいことはわかる
背理法使ってる証明はココロが掴めない

むしろつかめることが多いけど

背理法で体の拡大を考えるって意味わからん

背理法が全てが悪いんじゃなくて無根拠な排中律・排重律・排他律の適用が悪いんだけどな｡
とは言え背理法で囲い込んで特定されるより推論過程でピタリと特定される方がしっくり感は有る｡
まぁしっくり感も人間が感じるもんだから怪しむべきっちゃ怪しむべきなんだが｡
人は巷に広められた情報よりも自分で入手した情報を信じ易い、ってな｡
背理法にせよ帰納法にせよ自然結論にせよ、各証明は吟味が必要って事だな｡

>>276
無内容

ブーメラン自爆ご苦労。その無内容、と言うか可も無く不可も無い事実に気付かず
背理法要否を唱える人間や背理法濫用に気付かない人間が、どれだけ多い事か

>>278
恥の上塗り
内容のない長文を書いた自分を恥じよ

>>259
背理法の根幹は排中律だからってことでしょ
Pか～Pかしかないってことを使っている

そういう論理もあるってだけ

直観主義は直観的なのか？爆発律って直観的か？

アインシュタインは時間は幻想だと言っていた

でも　仮にそれが幻想だとしても　時計の針が逆向きに動くところなど

見たことが無い。。

でもそれは　「それが時計だから」だ

そもそも時計と言う物体はそういう風に作られている　逆になど動かない

前提の代物なのだよ。。　だがその事と　時間が逆行しない　という言説

とは科学的相関性は無い。。

>>282
>爆発律って直観的か？
そりゃ直感的だよ
空集合はすべての集合に含まれるってのが爆発律

爆発律って初耳だからググってみたら
「矛盾から全てが出る」の事じゃねーか

>>284
THX
何となくわかった

有と無を同列に扱ったが故の矛盾宿命…
だが有と無を隔てる理も無く…

背理法の代わりに対偶法を使えってこと？
￢Q→￢Pだと仮定するのは￢Qだけだけど
P∧￢Q→⊥ならPと￢Qとを仮定できるのでずっと見通しが良くなる

>>284
それは違うやろ

たぶん「命題x」と「xの証明全体から成る集合S(x)」、
「xならばy」と「写像S(x)→S(y)」を対応させる埋め込みを考えてるんだろうけど、
“矛盾を空集合に対応させていいのか”という問題がある

矛盾が証明できないという先見的な証拠はないし「真なる矛盾が存在する」という哲学的立場もある(真矛盾主義)

tan1°は有理数か

>>289
矛盾を何か神格化してるだけだなそれ

まーた哲学者が暴れてるよ
真なる矛盾なんかあるわけないだろ

背理法不要論はまあ背理法使うと公理を一つ余分に入れないといけない点から来てるんだろうと思うけど、
ZFなら正則性公理だってそれほど自然とは思えないんだけどな
ZFCなら排中律を証明できるんだっけ？

>>293
>正則性公理だってそれほど自然とは思えないんだけどな
え？
何が元か最終的にハッキリしない集合の存在を当然と思うかどうかよ
もちろんそういう集合が合ってもいいという立場も有り得るだろうけど
そっちを自然と感じる？

>>293
>ZFCなら排中律を証明できる
https://plato.stanford.edu/entries/axiom-choice/#AxiChoLog
ホントヶ？

真矛盾って肯定的証明も否定的証明も出来ない矛盾の事と違うたんか？

所で嘘吐きのパラドクスは不合理では有るが実は矛盾ではない｡
――貴方は貴方ですか？」正直 Y.
嘘吐 N.
――貴方は正直ですか？
正直 Y.
嘘吐 Y.

？？=(￢正直)or(￢嘘吐き)

――貴方は正直ですか？Take2
正直 Y.
嘘吐 Y.
￢正直 N.
￢嘘吐 N.
――貴方は貴方ですか？Take2」
正直 Y.
嘘吐 N.
￢正直 N
￢嘘吐 Y

>>295
この中で
∀X∀Y∀F(∀x(X(x)↔Y(x))→FX=FY)
を公理にしてるのがこの結論を導いてるようだけど
2階の関数ってこの性質を持つべきなのかな
定義は異なるが真偽が一致するX,Yに対して
FXとFYが必ずしも一致しないFを考えても良くない？

この証明のキモは
選択公理によって
Aの真偽と一致不一致が同値になる関数Kの存在が示せるというところ
Aの真偽を01に対応させる関数が存在することを示しているとも言えそう

ここにも基地外が出たか

背理法は便利だよ

背理法無しでtan1°が無理数であることを証明して

対偶による証明も背理法の一種だからなぁ。

愚かとしか思えないんだけど。

>>302
＞対偶による証明も背理法の一種だからなぁ。

そういう視点もあるよね
つまり
命題 P→Q
対偶 ￢Q→￢P
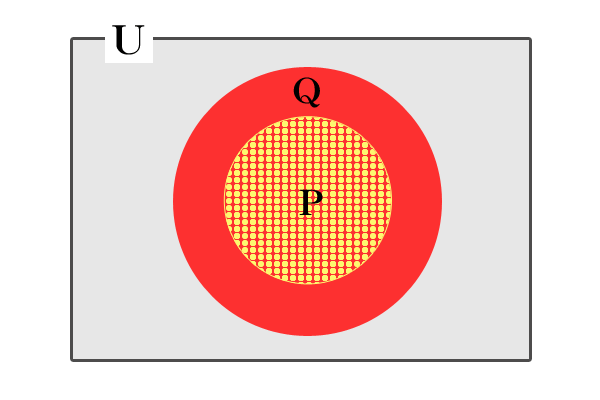
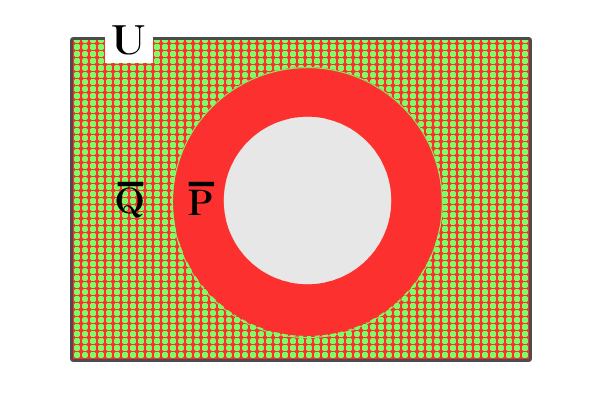
背理 ￢Q∧P→矛盾（集合のベン図で ￢Q∩P＝Φ（空集合））
（要するに、集合で考えると P⊂Q が成立つ ←→ ￢Q∩P＝Φ（空集合））
背理法の利点： ￢Q∧P と2つの条件が使えること。つまり、 対偶 ￢Q→￢P（１つの条件￢Q から ￢Pを導く）よりも、証明の筋道が見えやすい場合が多いってことが、大きな利点です
なので、背理法は非常に有用です！！

（参考）
https://kou.benesse.co.jp/nigate/math/a14m0119.html
進研ゼミ
【数と式】「pならばq 」が真のとき，集合Pが集合Qに含まれる理由

「 p ⇒q 」が真，つまり「 p ⇒q 」が成り立つ，ということをベン図に表してみましょう。
条件pを満たすもの全体の集合をP，条件qを満たすもの全体の集合をQとすると，Pに含まれているものx は，条件pを満たしています。今，「 p ⇒q 」が成り立っているのですから，xは条件qも満たしているということになり，xはQに含まれるのです。
つまり，Pに含まれているものはすべて，Qに含まれることになり，このことを集合のベン図で表すと，図１のようになります。

図１

うざい。死ね

>条件pを満たすもの全体の集合をP
“もの”って何？ラッセルのパラドックスぶつけるぞオラ

で？ どうしたの？ｗ

背理法って全然そうは見えないけど、実はワン・ツー狙いの
ロングクロスでサイドに張る隠れバックスって感じも

>>305
``もの''つまり要素になれるものはすべて集合、集合の集まりは一般にはクラス

背理背理笛背理法
背理背理笛方法
丸大ハンバーグ

>>307-308
同意

P→Qの証明を
迷路に例えると
１．正攻法：Pから出発して、愚直にQを目指す
２．対偶法：Qから出発して、逆にPを目指す
　（正確には、￢Pと￢Qの地図で、￢Q→￢P、つまり￢Qから出発して、逆から￢Pを目指す）
３．背理法：PとQから出発して、どこかの矛盾点（ゴール）を探す
　（正確には、Pと￢Qの地図で、どこかの矛盾点（ゴール）を探す）

問題毎に、正攻法、対偶法、背理法の３つで、最も適した（最も分かり易い）証明法があるだろう
勿論、背理法で証明された後なら、正攻法でPから出発して Qに至る道を見つけることは、容易なっているだろう

なので、背理法は有用と思うよ
Pと￢Qの二つの条件が明示されていることが、そのメリット（証明を考えるのに分かり易い場合がある）

無内容の長文

>>310-311
>無内容の長文

同意
まあ、「背理法は有用です」とか
「Pと￢Qの二つの条件が明示されていることが、そのメリット（証明を考えるのに分かり易い場合がある）」とか
ほぼ自明だからなーｗ

例えば、中学数学の例で、「√2は、無理数である」の証明
１．そもそも、”無理数の定義：実数Rの中で、有理数Q以外” なわけで、”有理数Qの定義：有理数体Q”ってこと
　だから、圧倒的に、有理数Qを出発点にする方が、無理数を出発点にするより、有利だよね
２．そこで、有理数Qは「a/b という分数で表せる数のこと」と、「√2の性質：二乗して2になる」と、2つの性質を組合わせて、矛盾を導くという方針が立つ
３．これぞ、背理法であり、極めて自然な証明法である

上記は、いろんな人がいろんな所で書いていることで、知る人ぞ知る、自明と言えば極めて自明なことだよ
上記は、中学数学の簡単な例だが
同じようなことは、数学のいたるところにある

（参考）
https://ja.wikipedia.org/wiki/%E6%9C%89%E7%90%86%E6%95%B0
有理数（ゆうりすう、英: rational number) とは、二つの整数 a, b （ただし b は 0 でない）をもちいて a/b という分数で表せる数のことをいう。
有理数ではない実数は無理数と呼ばれる。
基本性質
既に述べたように、通常の四則演算のもと、代数系 (Q, +, ×, 0, 1) は有理数体と呼ばれる体を成す。また、有理整数環 Z の商体である。

>>310
解る気がします
悪乗りですけど
守備は教えられるけど（フォワード）攻撃は教えられない現代サッカーの
視点に立てば、選手の誰もが均一のパスの能力を持つと想定し

① パスがつながればゴールを奪える
② ゴールが奪えないならパスがつながっていない
③ パスがつながっているのにゴールが奪えない　/矛盾

今まではウインガーでもセカンドトップでもサイドハーフでもバックスでも、
つねにセンターやサイドに張らず流動的な戦術の中でめまぐるしくポジションを
変えながら相手の裏をかくようにパスをつないでいく傾向が。こういったスペイン流パス回しでも今はホントありきたり。
往々にしてほとんどの場面で正攻法はすぐばれる気が

>>310
＞対偶法：Qから出発して、逆にPを目指す
＞（正確には、￢Pと￢Qの地図で、￢Q→￢P、
＞　つまり￢Qから出発して、逆から￢Pを目指す）

「Qから出発して、Pを目指す」のは
「￢Qから出発して、￢Pを目指す」のとは
全く違うけどね

対偶と逆を同じだと思ってる？
https://kou.benesse.co.jp/nigate/math/a14m0120.html

>>310
＞背理法：PとQから出発して、どこかの矛盾点（ゴール）を探す
＞（正確には、Pと￢Qの地図で、どこかの矛盾点（ゴール）を探す）

「PとQが矛盾する」のは
「Pと￢Qが矛盾する」のとは
全く違うけどね

Qと￢Qが同値だと思ってる？

>>314-315
全部同意ですよ
話を分り易く書いているのです
細かいところを、省いてね
というのは、この数学板では、もともと細かい緻密な議論は無理なのです
図も書けないしね

もう一度説明すると
１．証明を、迷路に例える
２．通常法はP→Q、つまりPを出発点として、ゴールQに辿り着ければ、証明が終わる
３．だが、Pを出発点として、Qの情報が見えない
４．対偶法は、￢Q→￢Pの迷路に直して、￢Qを出発点とした方が、ゴール￢Pへの道が分り易いとき有効
５．背理法は、￢QとPの2つの情報を使って、矛盾というゴールを探す証明手法

と、こういう説明なんだよ
通常法、対偶法、背理法の３つとも、正しい数学の証明法です
それぞれ、利害得失があるってこと

>>316 補足

背理法の話は、過去にガロアスレでも扱ったよ
下記 目玉焼き さんのコメントを読んでみて

現代数学の系譜 工学物理雑談 古典ガロア理論も読む53
http://2chb.net/r/math/1537363981/82-

URL アマゾン /dp/4903342220
背理法 (数学書房選書) 単行本 ? 2012/5
桂 利行 (著, 編集), 栗原 将人 (著, 編集), 堤 誉志雄 (著, 編集), 深谷 賢治 (著, 編集)
単行本: 128ページ
出版社: 数学書房 (2012/05)

目玉焼き
5つ星のうち5.0「構文」背理法を通して、排中律に重きを置く「こころ」を解説。
2012年10月21日
この本のタイトルである背理法という間接証明法はラディカルな批判者によって一時期不当な評価をされていましたが、現在は議論も一回りし決着が付いているようですのでレビューを書き直しました。

一つ、脱背理法論者の理論の決定的な間違いを指摘しておきましょう。
以下略

>>317 補足の補足

かつて、下記みたいな話があったので
このスレが、あるのでしょうね（>>1ご参照）

（参考）
http://abel.a.la9.jp/sub11.html
東京理科大学理学部第一部数学科　教授　安部直人
背理法被害者の会 - 安部研究室
安部研究室HP
脱背理法教育(01) 2013/07/
(抜粋)
(通常背理法で証明される定理を背理法を用いず証明する)を東京理科大学数学科で実践しています。
略

>>317
肝心なところを省略してどうする

>>318

もう少し書くと
下記安部研究室、”背理法無用：「√2 が無理数」の直接証明”と書いてあるけど
やっていることは、「P：x＝√2（x^2＝2）→Q：xは無理数」として
P→Qの証明下記で、「Pかつ￢Q→Φ（空集合）」ってこと（ここで￢Q：xは有理数）
つまり、>>303の「背理法 ￢Q∧P→矛盾（集合のベン図で ￢Q∩P＝Φ（空集合））」そのもの
（くどいが、「x^2＝2 かつ xは有理数 を満たすxは存在しない」を示しているだけなのです）
それを示すのに、因数分解の一意性という大定理を使っているだけのこと
そういう見方もできるよね

（参考）
http://abel.a.la9.jp/index.html
東京理科大学理学部第一部数学科　教授　安部直人
背理法被害者の会 - 安部研究室
安部研究室HP
脱背理法教育(01)2013年02月23日
(抜粋)
　背理法無用：「√2 が無理数」の直接証明：
　「自然数　a,b につき、
　aa と 2bb の素因数の個数は偶数と奇数
　で異なるから aa≠2bb、よって √2≠a/b。」
(不要かもしれませんが少し説明を加えます。
　a と b を素数の積で表したとき、その素数(素因数)の個数をそれぞれ s と t とすれば、aa と 2bb の素因数の個数は s+s=2s と 1+t+t=2t+1 です。
　また、2＝(a/b)^2 から √2≠a/b を導くのに背理法を使っていると疑う人がいるので、
　x,y>0 のとき、√x＝√y と x＝y は同値
ですから、　√x≠√y と x≠y も同値です。)
[背理法でもっと簡潔に証明できますか？]
　また、素因数分解の存在と一意性も勿論背理法を用いず証明できます。

>>319
いや、引用すると、かなり長くなるんだ

>>320

さらに書くと
フェルマー予想
”3 以上の自然数 n について
x^n + y^n = z^n
自然数の組 (x, y, z) は存在しない、という定理”

証明される前は、予想だったから
当然、x^n + y^n = z^n の解があるとして、「あるとすれば、その解がどういう性質を持つか」という筋が自然に浮かぶだろう
それが、結果的に、背理法の証明に繋がった

つまり、”自然数の組 (x, y, z) は存在しない”→自然数の組 (x, y, z) が存在する→x^n + y^n = z^nの解を調べる→矛盾→背理法の証明完成 となる
それって、真っ当な数学の手法でしょ？
そういう（自然に背理法を使う）数学の対象が、あるってことです

（参考）
https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A7%E3%83%AB%E3%83%9E%E3%83%BC%E3%81%AE%E6%9C%80%E7%B5%82%E5%AE%9A%E7%90%86
フェルマーの最終定理
(抜粋)
3 以上の自然数 n について
x^n + y^n = z^n
自然数の組 (x, y, z) は存在しない、という定理のことである[注釈 1]。
長らく証明も反証もなされなかったことからフェルマー予想とも称されたが、フェルマーの死後360年経った1995年にアンドリュー・ワイルズによって完全に証明され、ワイルズの定理あるいはフェルマー・ワイルズの定理とも呼ばれるようになった[1]。
目次
1 概略
2 個別研究の時代
2.1 n = 4：フェルマー
2.2 n = 3：オイラー
2.3 n = 5：ジェルマン、ディリクレ、ルジャンドル
2.4 n = 14 ：ディリクレおよび 7 ：ラメ、ルベーグ
2.5 クンマーの理想数

>>316
＞分り易く書いているのです
＞細かいところを、省いてね

￢の有無を「細かいところ」という人ははじめて見た

実に粗雑ですね

＞数学板では、もともと細かい緻密な議論は無理なのです
＞図も書けないしね

￢は図でなく文字ですけどね

出し方知らない？教えてあげますよ

”のっと”と打って変換すれば出ますよ

￢なんて全然細かくないし緻密でもないですけどね

>>323
フォローありがとう
まあ、おれからすれば、こんな話は、各人それぞれが納得すれば良いだけのことだが
「背理法被害者の会」も、きちんと否定（￢）しておきたいと思ったから書いただけのことよ

>>323
>＞図も書けないしね
>￢は図でなく文字ですけどね

いや、そういう意味じゃなく
ベン図とか、ポンチ絵とか、書けば分り易いと思うのだがね
それが、この板では書けない
（例えば、２～３行に渡る斜め矢印とかも書けないから、全てを１行で済ませるしかない。ＪＰＧとかを他にアップしてリンクするのもあるけど、かったるいしね）

そういうことを、言っているのだよ

星座の絵だけ教えて星の配置を教えない説明。
わかってる人が分かりやすく説明しようとして、
かえって分かりにくくなるよくあるパターン

>>326
いや、仰る通りだよ
まあ、所詮この板では限界があるとは、思っていて、100人の100人に分からせるためには、本一冊いるかも
実際に、>>317の通り本があるし、それ嫁ってこともある

まあ、言いたいことは>>317の書評にもあるように
背理法が自然な数学の対象があるってこと（>>322）

逆に、背理法がまずい場合もあるよね
例えば、「ある式f(x)=0が、有理数解を持つことを示せ」という問題があったとして
背理法を使う人はいないだろう

背理法で、「ｘが有理数でないとして・・」と議論を進める人はいない
ｘが有理数として、x=a/b と置いて、f(a/b)=0 で式変形をするとかが、普通でしょ
かように、普通にP→Q、対偶 ￢Q→￢P、背理法 ￢Q∧P→Φ（空集合） or 矛盾

それぞれ、利害得失がある
それぞれの特徴を知って
うまく使い分ければ良いってこと。背理法を排除する必然性なしってこと

まあ、数学教員になる人もいるだろうから貼る
あんまり、良い資料とも思えないけど、何かの参考にはなるだろう

https://ir.lib.hiroshima-u.ac.jp/files/public/4/43403/20170629113159591483/AnnEducRes_45_281.pdf
広島大学 学部・附属学校共同研究機構研究紀要
〈第45号 2017.3〉
間接証明カリキュラムの開発に関する研究
―背理法の学習過程に注目して―
早田 透 上ヶ谷 友佑 袴田 綾斗 岩知道 秀樹
影山 和也 小山 正孝 寺垣内 政一

>>327 補足
下記のPDFがヒットしたので、貼っておくが
下記にもいろいろ書いてあるけど

典型的な、「√2は無理数である」ことの証明
つまり
P：x=√2 → Q：xは無理数 の証明
これは、「 ”x^2=2” ∧ ”xは有理数" → Φ（空集合）：x^2=2は有理数解を持たない」・・(1) を証明すれば良いという言い換えができる

では、どうすれば、この言い換えを思いつくかというと、背理法なら ￢Q∧P→Φ（空集合） ですんなり出る
　>>320の安部先生がやっていることも
上記(1)の証明に、自然数の因数分解を使っているだけのことです。それで「脱背理法」とかは言えない

さらに、”Q：xは無理数”に注目すると、”￢Q：xは有理数”に書き直した方が、圧倒的に証明しやすいということ
そして、”P：x^2=2”も、同時に証明の最初から使っていきたいのです
そういう数学的構造が背景にあるから、背理法がうまくマッチするのです

つまり、背理法がうまくマッチする数学的対象あるってことです
（因みに、対偶法は相応しくない。例えば （対偶法） ”￢Q：xは有理数” → ”￢P：x=√2は解を持たない”ってことだけど、そんな証明は迂遠ですね ）

だから、直接証明、対偶法、背理法、それぞれに利害得失があって、適した証明法を選ぶってこと
もちろん、背理法の証明を、直接証明に直すことは可能です
でも、証明を迷路に例えると、如何に見通しよくゴールに辿り着けるかってことで、いろんな手法があっていいのです。背理法を排除するのは、間違い！

（参考）
http://www.st.nanzan-u.ac.jp/info/ma-thesis/2013/KSASAKI/m12mm007.pdf
推論を適切に選択するための数理的手法 M2012MM007 堀場康行 指導教員：佐々木克巳 修士論文要旨 情報分析科学分野 2013
http://www.st.nanzan-u.ac.jp/info/ma-thesis/2013/
南山大学大学院 数理情報研究科 2013年度 修士論文・OJL報告書要旨集

>>329 補足の補足
>つまり、背理法がうまくマッチする数学的対象あるってことです
>（因みに、対偶法は相応しくない。例えば （対偶法） ”￢Q：xは有理数” → ”￢P：x=√2は解を持たない”ってことだけど、そんな証明は迂遠ですね ）

要するに、対偶法では、x=√2はゴールです
しかし、x=√2は証明のスタートから使いたいのです
その点、背理法では、x=√2（つまり P：x^2=2） は、スタートなのです
単純なようで、この点は、大きな違いなのです

>>329
>（対偶法） ”￢Q：xは有理数” → ”￢P：x=√2は解を持たない”
>ってことだけど、そんな証明は迂遠ですね

xは有理数　⇒　(x^2<2∨x^2>2)　なら　意味あるね

>>331
同意
まあ、証明において、何事もそうだが
最初の証明のあとに
いくつもの、別証明が出てくることがあるよね
その1つとしての意味はあるだろうね

背理法で使う「仮定」が一つに見えても、
実際は論理の連鎖の過程で別の「仮定」が知らずに紛れ込むことがあるから
背理法は極めて危険な論法と言わざるを得ない。

>>333
それ
照明全般についての注意ってこと気が付いてないみたいな

>>333-334

ああ、そうだね
でも、そういう証明の失敗が、数学の進歩に繋がることも多いのも、また事実

下記、ラメとコーシーの証明の失敗から、”虚数レベルでの一意的な因数分解”が考察され、理想数の理論からイデアルの理論が生まれた如く
だから、背理法でも、ともかくも、証明を前に進めるということは大事だね

勿論、正しい証明で拍手喝采が理想だけれども、
数学の歴史を見ると、何度かの失敗の後に、証明が完成することも多い

https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A7%E3%83%AB%E3%83%9E%E3%83%BC%E3%81%AE%E6%9C%80%E7%B5%82%E5%AE%9A%E7%90%86
フェルマーの最終定理

1847年、ラメは「フェルマー予想の一般的解法を発見した」と発表し、同じ解法を自分の方が先に発見していたと主張するオーギュスタン＝ルイ・コーシーとの間で論争にまでなった。しかしこの解法とは xn + yn = zn の左辺を複素数で素因子分解するというものであり、この分解は一意的なものでないためこの問題に関する解法たりえていないことが指摘される[15]。

クンマーの理想数
コーシーとラメが争っていたのと同じ頃、エルンスト・クンマーが自ら打ち立てた理想数の理論（後にリヒャルト・デーデキントがイデアルの理論として発展させる）を導入する[16]。
これにより、多くの素数において一意的な因数分解が可能となり、n が正則素数である（もしくは正則素数で割り切れる）全ての場合については証明がなされた[17]。
虚数レベルでの一意的な因数分解が不可能な非正則素数も無限に存在する[注釈 6]が、クンマーは 100 以下の非正則素数（37, 59, 67 の 3 個しかない）についてはそれぞれ個別に研究して解決した[19]。
その結果、100 までの全ての奇素数 n について（当然 100 以下の奇素数を約数に持つ全ての n についても）フェルマー予想が成り立つことが証明され、それまでの個別研究からこの問題は大きく飛躍した。

>>335
>>142で既出

>>336
ご指摘ありがとう

背理法不要論の人、教授だからな
お前らより完全に格上だからな

権威主義っぽい(格上であったとしてそれは正当性を保証しない。教授などのポストを持つ人が完全に誤ったペーパーを出したりすることは珍しくない)

>>338
つーかその人なんで不要と言い始めたの？

>>340
背理法が正しいと都合が悪いから
科学なんて捨てていい奴なんてどうでもいい

素因数分解可能ということや素因数分解の一意性って
背理法でなくて証明したらエラい長くならない？

PならばQを示す代わりにPかつ￢Qならば矛盾を示すのが良くない理由として結局正しくない￢Qを仮定するからと言っているけれどならば対偶法は￢Qならば￢Pを証明するんだから￢Qを仮定するのみならず結論としてそもそも正しくない￢Pを導くという欺瞞

人間は全称命題を知覚することは不能であるから
その否定の特称命題を証明する他ない
また全称量化子の元を全称のまま選ぶことはできるが
ある特定の元として選ぶことはできない
つまり全称命題は間接証明しかできないのであるから
その間接法である対偶法を用いることになるのである

>>344
2番目の文章はおかしいように思う
どういう意味で言ってるの？

>>343
まず背理法は正しいことが証明されている
否定したいなら正しくないと証明しないといけない

>>346
だから
背理法否定論者の主張が対偶法にも当てはまるのにそれは使っていいと言っているのが欺瞞だって言ったわけ

頭の中の数学モデルで考えるとき背理法の証明はどうイメージしてる？
私は背理法で証明するときは頭の中が文字と記号だけになる。

【政府が隠す３．１１】　地震波形が、核実験と同じ
http://2chb.net/r/earth/1575170033/l50

>>338
数学では、格上も格下もないよ（＾＾；

>>343
>PならばQを示す代わりにPかつ￢Qならば矛盾を示すのが良くない理由として結局正しくない￢Qを仮定するからと言っているけれどな

「正しくない￢Qを仮定する」って、違うと思うよ
実数R中で、Q：「Xが有理数」 で、￢Q：「Xが”有理数でない”＝無理数」ってことで、
（￢Qは実数R中の余事象ですよね）
「正しくない￢Qを仮定する」ではないよね

背理法の問題は、否定を仮定するとあら不思議と矛盾が出てくるけど、どこに無理が生じたのかが見えづらいこと

>>338
ヒルベルトより格上とはすごいねー

「数学から排中律を奪うのは,天文学者から望遠鏡を,ボクサーから拳を奪うようなものだ」

>>351
俺が言ってるんじゃなくって背理法不要論者がそう言ってるのよ

>>352
>否定を仮定すると
これが無理だったってことだわ

>>354
>俺が言ってるんじゃなくって背理法不要論者がそう言ってるのよ

　ID:kScGeWtOさんが、>>343や>>347で書いているけど
「正しくない￢Q」という主張が、おかしいわけですね（背理法不要論者たち）
それは、下記の高校数学で教える 「対偶」についての集合の包含関係による説明を見れば、一目瞭然です

（参考）
https://www.hmathmaster.com/math1/%E5%AF%BE%E5%81%B6%E3%81%AE%E8%A8%BC%E6%98%8E%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6/
高校数学マスター
対偶の証明について ２０１９年３月２９日
(抜粋)
【目次】
１．集合の包含関係を用いた証明
１－１．命題の推論関係と集合の包含関係が一致
１－２．補集合と包含関係の逆転

(p⇒q)⇔P⊂Q・・・(2)
が成立します。
ベン図を書くと、以下のようになります。


補集合と包含関係の逆転
見方を変えて、集合Pと集合Qのそれぞれの補集合に注目すると、以下のように包含関係が逆転していることが分かります。


つまり、
￢Q⊂￢Pであることが分かり、ここから、
￢Q⊂￢P⇔P⊂Q・・・(3)
が成り立ちます。
(2)と同様に、
(￢q⇒￢p)⇔￢Q⊂￢P・・・(4)
であることも分かり

>>316 補足

　>>316に書いた程度のことは、英文版の背理法wikipediaに書いてあるよ
なお、
”Proof by contradiction”：背理法
”Proof by contrapositive”：対偶法
です

（参考）
https://en.wikipedia.org/wiki/Proof_by_contradiction
Proof by contradiction
(抜粋)
Relationship with other proof techniques

In the case where the statement to be proven is an implication A → B, then the differences between direct proof, proof by contrapositive, and proof by contradiction can be outlined as follows:

・Direct proof: assume A and show B.
・Proof by contrapositive: assume ￢ B and show ￢ A.
　This corresponds to the equivalence A → B ≡ ￢ B → ￢ A.
・Proof by contradiction: assume A and ￢ B and derive a contradiction.
　This corresponds to the equivalences A → B ≡ ￢ ￢ (A → B) ≡ ￢ (A → B) → ⊥ ≡ (A ∧ ￢ B) → ⊥ .

>>312
> 有理数Qは「a/b という分数で表せる数のこと」

有理数の非循環節の長さは決定番号に成り得るわけでスレ主の数学では
成り立たないのだからスレ主にとっては間違いでしょ

>>358
意味が分からない
皆さんに分かるように、詳しく書いてみなさい

>>358
>>312
> 有理数Qは「a/b という分数で表せる数のこと」
>有理数の非循環節の長さは決定番号に成り得るわけでスレ主の数学では
>成り立たないのだからスレ主にとっては間違いでしょ

私、ガロアスレのスレ主は、下記の定義
「有理数（ゆうりすう、英: rational number) とは、二つの整数 a, b （ただし b は 0 でない）をもちいて a/b という分数で表せる数のことをいう」
は否定してはいない
「成り立たない」と言っているのは、時枝記事の数当て論法だよ
時枝記事の数当て不成立は、下記を「現代数学の系譜　カントル　超限集合論2 357」以降を見て下さい

（参考）
現代数学の系譜　カントル　超限集合論2
http://2chb.net/r/math/1576852086/357-

https://ja.wikipedia.org/wiki/%E6%9C%89%E7%90%86%E6%95%B0
有理数

有理数（ゆうりすう、英: rational number) とは、二つの整数 a, b （ただし b は 0 でない）をもちいて a/b という分数で表せる数のことをいう。b = 1 とすることにより、任意の整数は有理数として扱うことができる。

有理数を十進法などの位取り記数法を用いて小数表示した場合、どの有理数も位取りの基数のとり方に関わらず有限小数または循環小数のいずれかとなる（もちろん、ある基数で表示したとき有限小数となる有理数が、別の基数では循環小数となったりすること、あるいはその逆になることはある）。同様に、有理数は必ず有限正則連分数展開を持つ。

>>358
混ぜっ返しで、あなたには、下記 筑波大 山崎 隆雄 先生 『ｐ-進世界へようこそ』を、プレゼントします
どぞｗ（＾＾；

（参考）
https://nc.math.tsukuba.ac.jp/index.php?action=pages_view_main&;block_id=206&active_action=multidatabase_view_main_detail&content_id=21&multidatabase_id=3&block_id=206#_206
筑波大 過去の体験学習
年度 平成１７年度
日付 平成１７年８月４日(木)
概要
『ｐ-進世界へようこそ』
山崎 隆雄 先生
https://nc.math.tsukuba.ac.jp/index.php?action=cabinet_action_main_download&;block_id=282&room_id=80&cabinet_id=1&file_id=6&upload_id=202
p-進世界へようこそ
山崎 隆雄
筑波大学数学系

2 2-進世界を覗いてみる
それでは始めに p = 2 の場合、つまり 2-進世界がどのような世界なのか、少しだ
け覗いてみましょう。一つの極めて特徴的・刺激的な事実は、2-進世界では次の式
が成り立つことです：
1 + 2 + 4 + 8 + 16 + ・・・ + 2^n + ・・・ = ?1 (1)
私はこれを、比喩的に成り立つとか心情的に成り立つと言っているのではありま
せん。2-進数の世界では、この式が１００％精密な意味で成り立つのです。これは
かなり奇妙に感じられることでしょう。全くでたらめな世界だと感じられるかも
しれません。

>>360
>時枝記事の数当て不成立は、下記を「現代数学の系譜　カントル　超限集合論2 357」以降を見て下さい
おまえのレス、すべて否定されてて、それに対しおまえ反論できてないじゃん
不都合なレスを黙殺して勝手に勝利宣言するサイコパス（＾＾；

>>360
たとえば100個の箱に有理数がそれぞれ1つ入っている場合にそれぞれが分数で表されるのならば
分母(全て異なると仮定する)が最大である有理数が入っている箱を選ばない確率は計算できるでしょ
(分数であらわされるのならば分母は必ず整数で与えられる)

スレ主の理屈だと「裾が発散する超ヘビーな（裾の超重い）分布」だと箱の中身が有理数であっても
分数で表されないから上の確率も計算できないということになるじゃないですか

>>362-363
おまいらの屁理屈笑える
それって、哀れな素人氏 と類似の屁理屈（下記）じゃんかｗ

（説明）
・いま、ここに1つの箱がある。箱に任意の実数r∈Rを入れて良い
・なんの手がかりも、無ければ、箱の数当ては無理。的中確率は、0＝1/∞。測度論でいう零集合から従う
・いま、有限で複数の箱(n個)があるとする。iid(独立同分布)を仮定する。どの箱も他の箱と無関係だ
　X1,X2,・・,Xi,・・Xn で、任意のi を残して、他の箱を開けたところで、Xiを的中させる手がかりはない。なので、上記箱が1つの場合に同じ
　（∵ iid(独立同分布)だから）
・n→∞（可算無限）で、考える。確率変数の無限族 X1,X2,・・,Xi,・・Xn,・・・ は、現代確率論・確率過程論の射程内だ
・よって、n→∞（可算無限）でも、n有限と結論は同じですよｗ
QED

なお
続きをやりたければ、現代数学の系譜　カントル　超限集合論2 へ書け！ ｗ（＾＾
http://2chb.net/r/math/1576852086/

（参考）
0.99999……は１ではない　その５
http://2chb.net/r/math/1583048263/1
1 名前：哀れな素人[] 投稿日：2020/03/01(日) 16:37:43.62 ID:DX1hheTs [1/3]
(抜粋)
簡単な証明１
１÷３は永遠に割り切れない。
ゆえに1/3≠0.33333……
ゆえに1≠0.99999……
もっと深いことが知りたい人は
「相対性理論はペテンである／無限小数は数ではない」参照

https://ja.wikipedia.org/wiki/%E7%8B%AC%E7%AB%8B%E5%90%8C%E5%88%86%E5%B8%83
独立同分布（どくりつどうぶんぷ、英: independent and identically distributed; IID, i.i.d., iid）

（確率変数の無限族の例）
http://web.econ.keio.ac.jp/staff/hattori/probe.htm 講義録等講義関係資料 (pdf files) 秋学期講義スライド 　(0.4MB pdf file)
http://web.econ.keio.ac.jp/staff/hattori/ecproc.pdf
確率論入門II 服部哲弥 慶応
P26
無限回硬貨投げの空間が必要な理由

https://www.wikiwand.com/ja/%E6%B8%AC%E5%BA%A6%E8%AB%96
測度論
可測集合 S が μ (S ) = 0 であるとき零集合 (null set ) という。
以上

>>365
> n→∞（可算無限）でも、n有限と結論は同じですよｗ

非循環節の長さが有限ならば有理数で分数で表せる
非循環節の長さが可算無限ならば無理数で分数で表せない

有理数と無理数は異なる
有限と無限は異なる

さて分かりやすくするために実数から有理数を選んでgame2を行うとして
出題者は無理数を選んだら即負けとなる場合に独立同分布では循環節は選べないのに
どうやって出題者は有理数を選ぶのでしょう？

> 屁理屈

違いますよ
可算無限は自然数全体の集合の濃度で定義されているので
個別の箱を考えると可算無限は扱えないのです

>>365
スレ違いだよ
ここは、背理法スレだよ

>>364
>・n→∞（可算無限）で、考える。確率変数の無限族 X1,X2,・・,Xi,・・Xn,・・・ は、現代確率論・確率過程論の射程内だ
時枝戦略は現代確率論・確率過程論の射程外ですね。
実際、時枝戦略における確率変数は k∈{1,2,...,100} なので、無限族論法はまったく的外れですね。
時枝戦略を論ずるなら時枝戦略を正しく理解することから始めましょう（＾＾；

>>366

>>364
> 無限回硬貨投げの空間が必要な理由
> n→∞（可算無限）でも、n有限と結論は同じですよｗ

スレ主の主張
game2は不成立であってその理由は
独立同分布で無限回試行をおこなって有理数を選べる
またその選んだ数は(有理数なので)分数であらわせる

> 背理法スレだよ

スレ主の主張が正しいと仮定する
コイントス(0と1の2つの数)であってもその無限回試行全体は非可算無限集合である
有理数全体は可算無限集合であるから矛盾が生じる

無限降下法も背理法の一種だけどこれも否定派なの？

ベルヌーイ試行の全体が非可算無限だなんて
どんなトンデモだよ

このスレの>>1でもないのにスレ主と呼んでいる時点であの阿呆の術中にはまっている

だいたいスレ主というの自体自称にすぎないんだな
そんなものはオラン

>>371-372
「瀬田」という名前らしいから
そう呼んであげると尻尾振って喜ぶよ

http://2chb.net/r/math/1411454303/200-202

"file:///C:/Users/seta/AppData/Local/Temp/1902_Sylow.html"

>>372
>だいたいスレ主というの自体自称にすぎないんだな
>そんなものはオラン

それは正しいよ
なお、ガロアスレが無くなったから、空き家の下記を代用することにしたよｗ(゜ロ゜;

現代数学の系譜　カントル　超限集合論2
http://2chb.net/r/math/1576852086/

>>373
私は、名前の議論には乗りません
議論をすることが、誰か第三者の迷惑に成りかねないからね

ところで、このID:VaJI+BR1氏＝”おサル”の紹介をしておく
おサルは、時枝記事（下記）前段の数当てパズルを正しいと信じている落ちこぼれです
某テイ大数学科卒 らしいが、確率論の単位を落としたらしい

時枝記事では、「確率変数の無限族 X1,X2,・・,Xi,・・において
あるXiが存在して確率1-εで的中できる」とする 数学パズルを正しいと信じているのです
確率論を学べば、iid（独立同分布)を仮定すれば、そんなXiは存在しようがないことは自明です

だが、おサルさんは、「時枝記事が否定されれば、選択公理が否定される」と名言?を主張するのです
それって、”選択公理”とか、”数学の推論”等で、完全に スベッている発言じゃないですか？ｗ(゜ロ゜;

（参考）
https://www.nippyo.co.jp/shop/magazine/6987.html
数学セミナー 　2015年11月号
箱入り無数目───────────────時枝 正　36

現代数学の系譜　カントル　超限集合論2
http://2chb.net/r/math/1576852086/358-
以上

>>375
>某テイ大数学科卒 らしいが、確率論の単位を落としたらしい
あなた The Riddle の成立は認めますね？
The Riddle は確率そのものを使ってませんから確率論の単位は無関係ですね。

>時枝記事では、「確率変数の無限族 X1,X2,・・,Xi,・・において
時枝戦略の確率変数は箱の中身ではなく 列番号k∈{1,,...,100} です。

>あるXiが存在して確率1-εで的中できる」とする 数学パズルを正しいと信じているのです
>確率論を学べば、iid（独立同分布)を仮定すれば、そんなXiは存在しようがないことは自明です
ある箱の中身を確率1-εで的中できるわけではありません。当たりの箱を確率1-εで選べるのです。
確率変数の取り方を誤解しているのに「数当てできる」という結果だけ使うからおかしな話になってるだけのことです。

>だが、おサルさんは、「時枝記事が否定されれば、選択公理が否定される」と名言?を主張するのです
>それって、”選択公理”とか、”数学の推論”等で、完全に スベッている発言じゃないですか？ｗ(゜ロ゜;
時枝戦略の仮定は選択公理だけなので、戦略を不成立とするには選択公理を偽とする以外ありません。

時枝戦略について論じたいなら、正しく理解することから始めましょう。

>>376
おサルさん、スレ違いだよ
ここは、背理法スレだよ

（参考：時枝関係）
現代数学の系譜　カントル　超限集合論2
http://2chb.net/r/math/1576852086/358-

現代数学の系譜11 ガロア理論を読む10
>274 ：１３２人目の素数さん：2014/10/19(日) 11:24:32.65
>同値類とか商集合も分かってなさそう
↑
時枝を理解できない原因が既にこの頃から言われてて草
はい、5年半経っても未だ分かってませんｗ

>>375
> iid（独立同分布)を仮定すれば、そんなXiは存在しようがない
> ことは自明

結局自明でごまかすことしかできないのね

>>364
> 有限で複数の箱(n個)があるとする
> Xiを的中させる手がかりはない
> （可算無限）で、考える

手がかりはありますよ
それは箱が可算無限個あってその全てに実数が入っているということ

箱の数が有限か無限か分からない場合に「iid（独立同分布)」を仮定して
ある1つの箱に着目しても有限か無限かは分からない

それでいつものガセ田のガセによってごまかすしか手がない
> よって、n→∞（可算無限）でも、n有限と結論は同じ

>同値類とか商集合も分かってなさそう
同値類、商集合が分からないと The Riddle は理解できない。
逆に The Riddle が理解できるなら、その主張は「100列のうちハズレ列は1列以下」なのだから、
時枝定理「100列のいずれかをランダムに選択すれば数当て失敗の確率は1/100以下」も理解できる。
すなわち「時枝定理＝The Riddle+小学生レベルの確率」でしかない。大学4年の確率論？まったく見当違いだ。

瀬田が The Riddle に対する態度を頑なに明かさないのは、確率論という屁理屈ネタが封じられるのと、
同値類、商集合に対する無知に触れられたくないからである。

瀬田は今後も同値類、商集合を勉強することはないだろう。
5年半も前（時枝記事登場よりも前）に指摘されていたにもかかわらず放置していることからも明らかだ。
↓
現代数学の系譜11 ガロア理論を読む10
>274 ：１３２人目の素数さん：2014/10/19(日) 11:24:32.65
>同値類とか商集合も分かってなさそう

結論
瀬田は学部レベルの数学が分かっておらず、時枝記事を読むレベルにない。今後も勉強する見込みは無い。

>瀬田が The Riddle に対する態度を頑なに明かさないのは、確率論という屁理屈ネタが封じられるのと、
>同値類、商集合に対する無知に触れられたくないからである。

予言しよう、瀬田は今後も The Riddle から逃亡し続けると

>>369
>無限降下法も背理法の一種だけどこれも否定派なの？

無限降下法も有用です
（参考）
http://www.mathlion.jp/article/ar139.html
2019/08/05
無限降下法|思考力を鍛える数学
(抜粋)
無限降下法とは 無限降下法(むげんこうかほう)とは， 自然数あるいは自然数の部分集合には必ず最小の元が存在する という性質を用いた証明法です．
... 代表的には，不定方程式の自然数解の不存在性を証明するときに用いられます．

https://ja.wikipedia.org/wiki/%E7%84%A1%E9%99%90%E9%99%8D%E4%B8%8B%E6%B3%95
無限降下法
(抜粋)
背理法の一種であり、数学的帰納法の一型とも見なせる。17世紀の数学者ピエール・ド・フェルマーが創始者であり、彼はこの証明法を好んで用いた。紀元前3世紀にユークリッドが（例えば『原論』7-31で）使用していた、との主張もある[要出典]。

概要
自然数に関する命題の証明に威力を発する場合があり、典型的には不定方程式に自然数解が存在しないことを示す際に用いられる。
小さい解を次々に得る様子が「無限に降下」していくように感じられることから、「無限降下法」と呼ばれる。

この証明のポイントは、最も「小さい」ものが存在するはずの、性質の良い「大小関係」を考えることである。必ずしも解そのものの大小関係である必要はなく、解に対してある自然数を対応させる関数の値の大小関係であれば十分である。

歴史
フェルマーは、無限降下法をしばしば「私の方法」と呼び、この方法によって数々の命題を証明したと主張した。彼は詳しい証明をほとんど残していないが、『算術』への45番目の書き込みにおいて、唯一完全に近い証明を残している[1][2]。

この証明中に、不定方程式 x^4 - y^4 = z^2 が非自明な整数解を持たないこと（これよりフェルマーの最終定理の n = 4 の場合が導かれる）を、無限降下法によって示している。

フェルマー以後も、無限降下法の考えはしばしば用いられている。たとえば、楕円曲線の有理点のなす群が有限生成アーベル群であることを主張するモーデルの定理の証明には、有理点の高さに関する、無限降下法と似た議論が用いられる[4]。

>>382
ある不定方程式が、自然数解を持たない
ということを証明する場合に

その方程式が、自然数解を持つとして
その解の性質を調べていくことは
数学として、自然な発想であり、自然な流れ
（ひょっとして 自然数解が見つかるかもしれないし、数学研究の場合には、自然数解が あるか ないか ハッキリしていない場合も多いのだし）

それを「背理法だから、ダメ」とか、何言っているの？（＾＾；

有限単純群の分類証明でも、最小の反例Gの存在を仮定して、矛盾を導く背理法を使う
普通、「ｘｘを満たす解は存在しない」ということを示すために、「ｘｘを満たす解が存在する」として、
その解の性質を調べるとか、あるいは矛盾が生じないかを調べるのは、数学研究の常套手段だ
それを、否定する理由は全くないと思う

https://www.jstage.jst.go.jp/article/sugaku1947/34/3/34_3_193/_pdf/-char/ja
論説 有限単純群の分類 鈴木通夫* 数学 1982 Volume 34 Issue 3 Pages 193-210
P13
分類の基本定理は 次のFeit-Thompsonの定理である.

以下Gは 分類定理にあげられた単純群のいずれとも同形でない最小位数の単純群と仮設する.
この仮設から矛盾を導くのが目的である.
定理3.最小の反例Gは連結な単純群である.

https://ja.wikipedia.org/wiki/%E6%9C%89%E9%99%90%E5%8D%98%E7%B4%94%E7%BE%A4%E3%81%AE%E5%88%86%E9%A1%9E
有限単純群の分類

目次
1 分類定理の主張
2 有限単純群の一覧
2.1 位数の小さな非可換有限単純群の一覧
3 分類定理の概観
3.1 小さな階数2の群
3.2 成分型の群
3.3 標数2型の群
3.4 単純群の存在と一意性

https://en.wikipedia.org/wiki/Classification_of_finite_simple_groups
Classification of finite simple groups

>>383
>ある不定方程式が、自然数解を持たない
>ということを証明する場合に

例えば、フェルマー予想
a^n + b^n = c^n n≧3
で、これを満たす整数解があるとして、下記の通り ABC予想から
互いに素な自然数 a, b, c の存在範囲が、有限範囲に絞り込める
その範囲を、計算機で調べれば、任意のｎについて、フェルマー予想 の別証明が得られる
（下記では、”ε = 1 のとき K(1) = 1 という予想”が成立てば、「この仮定の下で、指数が 6 以上の場合は直ちに証明される」という）

これを、背理法だからと、排除する理由はない

https://ja.wikipedia.org/wiki/ABC%E4%BA%88%E6%83%B3
ABC予想
(抜粋)
2 得られる結果の例
得られる結果の例
abc予想を真だと仮定すると多数の系が得られる。その中には既に知られている結果もあれば（予想の提出後に予想とは独立に証明されたものもある）、部分的証明となるものもある。
abc予想がもし早期に証明されていたなら、得られる系という意味での影響はもっと大きかったが、abc予想が成立した場合に解決される予想はまだ残っており、また数論の深い問題と数多くの結び付きがあるので、abc予想は依然として重要な問題であり続けている。

フェルマーの最終定理
ただし指数が十分大きい場合（どの程度大きければよいかは K(ε) に依る）。
ある K(ε) が具体的に求まれば、有限個の例外を直接計算することにより、原理的にはすべての指数 ? 4 に対して証明が可能である。
ε = 1 のとき K(1) = 1 という予想もあり、この仮定の下で、指数が 6 以上の場合は直ちに証明される (Granville & Tucker 2002)[注 2]。

注 2^ abc予想が K = 1 かつ ε = 1 で正しければ、互いに素な自然数 A, B, C が A + B = C を満たすとき C < (rad ABC)^2 が成り立つ。
互いに素な自然数 a, b, c が a^n + b^n = c^n を満たすと仮定すると、a^n, b^n, c^n は互いに素より、A = a^n, B = b^n, C = c^n を代入して
c^n<( rad a^n * b^n * c^n)^2
が成り立つ。一般に rad x^n= rad x≦ x であるから、 ( rad a^n * b^n * c^n)^2≦ (abc)^2<(c^3)^2=c^6 となる。
ゆえに c^n < c^6, c > 1 より n < 6
n = 3, 4, 5 については古典的な証明があるので定理が証明される (山崎 2010, p. 11)

>>385

補足
https://ja.wikipedia.org/wiki/ABC%E4%BA%88%E6%83%B3
ABC予想
(抜粋)
参考文献
山崎, 隆雄「フェルマー予想とABC予想」 (pdf) 『数学セミナー』2010年10月、2012年9月19日閲覧。
(引用終り)

この上記 『数学セミナー』2010年10月は、間違い （正しくは、2010年12月号 下記）
かつ、リンク切れている

https://www.nippyo.co.jp/shop/magazine/5459.html
数学セミナー
2010年12月号　通巻 591号
発刊年月 2010.11
特集=続・解けそうで解けない問題
　多面体の展開図に関する未解決問題／並木誠…8
　フェルマーの最終定理とabc予想／山崎隆雄…13

なので、代用に 谷戸光昭先生の 下記を
http://yato.main.jp/
谷戸光昭のウェブサイト（授業・講義に関する情報 神奈工 ＝ 神奈川工科大学 (厚木市) 中央 ＝ 中央大学 (文京区) 明星 ＝ 明星大学 (日野市)）
http://yato.main.jp/koneta/koneta.htm
谷戸光昭 書き物置き場
http://yato.main.jp/koneta/ABC_conjecture.pdf
谷戸光昭 ABC予想について (2012/11/29)

どっかいけー

おまえが、このスレに来なければいいだけだろ？

何れにしろ無節操の無さを開き直るのは阿漕

開き直る？
意味わからん

自分の気に入らないから
「どっかいけー」とか、それ 運営以外には権利も権限ないよね

それがルール
一般人は、いやならスルーがルールでしょ？

と、自ら限度の無さを露呈

限度？
意味分からん

定義でしょ
5CHの？　定義を読みましょう～！

ん？背理法不要論＝対偶不要論＝排中律不要論と違うのか？
もしかして背理法って対偶以外の要素を含んでたりする？

>>393
ども

>もしかして背理法って対偶以外の要素を含んでたりする？

１．命題：Ｐ→Ｑ
２．対偶：￢Q→￢Ｐ
３．背理法：￢Q∧Ｐ→Φ（矛盾）

　つまり、集合Ｐ、Ｑで書くと
１．命題：Ｐ⊂Ｑ
２．対偶：￢Q⊂￢Ｐ
３．背理法：￢Q∩Ｐ＝Φ（空集合）

＞背理法不要論＝対偶不要論＝排中律不要論と違うのか？

排中律否定は、ブラウアーの直観論理ですね（）
これは、背理法不要論とは別です

つまり、いまの東京理科大を中心とする 背理法不要論 は、背理法は認めるけれど、不要だという
ブラウアーの直観論理は、背理法を否定するのです
分かり難いかもしれないが、そういうことです

（参考）
https://ja.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E7%9A%84%E7%9B%B4%E8%A6%B3%E4%B8%BB%E7%BE%A9
数学的直観主義
(抜粋)
来歴と評価
これに類する主張は、カントールの集合論に対抗する形で、クロネッカーやポアンカレによってもなされていたが、最も明確に表明したのは、オランダの位相幾何学者、ブラウワーである。
ブラウワーの立場に対してポアンカレらの立場は前直観主義と言われることがある。
ブラウワーは、数学的概念とは数学者の精神の産物であり、その存在はその構成によって示されるべきだという立場から、無限集合において、背理法によって、非存在の矛盾から存在を示す証明を認めなかった。
それ故、無限集合において「排中律」、すなわち、ある命題は真であるか偽であるかのどちらかであるという推論法則を捨てるべきだと主張し、ヒルベルトとの間に有名な論争を引き起こした。
ヒルベルトの形式主義は、直接的にはブラウワーからの批判的主張に対し排中律を守り、数学の無矛盾性を示すためのものと考えることができる[1]。

ブラウワーの主張は、感覚的で分かりにくかったが、その後ハイティング等によって整備され、結果的には古典論理から排中律を除いた形で形式化されたものが今日、直観主義論理として受け入れられている。
現代では直観主義論理は、数学の証明は全て構成的に為されなければならないという主張（数学的構成主義）と関連が深いと考えられている。

>>394　タイポ訂正

排中律否定は、ブラウアーの直観論理ですね（）
　↓
排中律否定は、ブラウアーの直観論理ですね

何か捻れとる

儂、最近あそこの「 0^0=1 ∵Bourbaki流集合論に基付き#{φ}^#{φ}=1である事ゆ因る 」に疑問｡
集合じゃろうとも同値類どんどんぶっ込み拡張されるじゃろ？

>>396
粋蕎さん、どうも

> 0^0=1

下記ですな

（参考）
https://ja.wikipedia.org/wiki/0%E3%81%AE0%E4%B9%97
0の0乗
(抜粋)
0 の 0 乗（ゼロのゼロじょう、英: zero to the power of zero, 0 to the 0th power）は、累乗あるいは指数関数において、底を 0、指数を 0 としたものである。その値は、代数学、組合せ論、集合論などの文脈ではしばしば 1 と定義される[注 1]一方で、解析学の文脈では二変数関数 xy が原点 (x, y) = (0, 0) において連続とならないため定義されない場合が多い。

[注 1]
1^ 0 と定義される場合もある。

目次
1 背景
2 1と定義される場合
2.1 モノイド論における扱い
2.2 集合論における扱い
3 定義されない場合
3.1 実解析における扱い
3.2 複素解析における扱い
4 コンピュータにおける扱い

>>397
あ否、其れも其うですが「背理法被害者の会」が主張しとる話です｡
「集合に於いてφ乗は只一つ」言い、更に
「竹内外史も『トポス』で『ブルバキ参照』」言っとります｡
こんなん「0乗は只、1」言うんと変わっとらんと思うんです｡

>>398
>あ否、其れも其うですが「背理法被害者の会」が主張しとる話です｡
>「集合に於いてφ乗は只一つ」言い

知っています
というか、過去にガロアスレで取り上げたことがある
”集合に於いて”という文脈が、判然としませんがねｗ（＾＾
まあ、下記でもご参考：>>397のwikipediaの英文版ですがね
ご注目は、”History of differing points of view”です
そして、各人が自分で判断すれば良いのでは？ｗｗ（＾＾

”集合に於いて”という文脈が、判然としませんが
デデキントの如く、ZFC：”自然数→実数→コーシー＆リーマンまでの解析”で、これZFCの射程とすれば
”集合に於いて”という文脈は、かなり小さい限定された範囲ですね（＾＾；

（参考）
https://en.wikipedia.org/wiki/Zero_to_the_power_of_zero
Zero to the power of zero
(抜粋)
Zero to the power of zero, denoted by 0^0, is a mathematical expression with no agreed-upon value. The most common possibilities are 1 or leaving the expression undefined, with justifications existing for each, depending on context.
In algebra and combinatorics, the generally agreed upon value is 0^0 = 1, whereas in mathematical analysis, the expression is sometimes left undefined. Computer programs also have differing ways of handling this expression.

History of differing points of view
The debate over the definition of 0^0 has been going on at least since the early 19th century.
At that time, most mathematicians agreed that 0^0=1, until in 1821 Cauchy[13] listed 0^0 along with expressions like 0/0 in a table of indeterminate forms.
In the 1830s Guglielmo Libri Carucci dalla Sommaja[14][15] published an unconvincing argument for 0^0=1, and Mobius[16] sided with him, erroneously claiming that lim t → 0^+ f(t)^g(t) ＝ 1 whenever lim t → 0^+ f(t)＝ lim t → 0^+ g(t)＝ 0 .
A commentator who signed his name simply as "S" provided the counterexample of (e^{-1/t )^t , and this quieted the debate for some time.

つづく

>>399

つづき
More historical details can be found in Knuth (1992).[17]

More recent authors interpret the situation above in different ways:
・Some argue that the best value for 0^0 depends on context, and hence that defining it once and for all is problematic.[18]
According to Benson (1999), "The choice whether to define 0^0 is based on convenience, not on correctness. If we refrain from defining 0^0, then certain assertions become unnecessarily awkward. [...]
The consensus is to use the definition 0^0=1 0^0=1, although there are textbooks that refrain from defining 0^0."[19]

・Others argue that 0^0 should be defined as 1. Knuth (1992) contends strongly that 0^0 "has to be 1", drawing a distinction between the value 0^0, which should equal 1 as advocated by Libri, and the limiting form
(an abbreviation for a limit of f(x)^g(x) where f(x),g(x) → 0 ),
which is necessarily an indeterminate form as listed by Cauchy
: "Both Cauchy and Libri were right, but Libri and his defenders did not understand why truth was on their side."[17]
Vaughn gives several other examples of theorems whose (simplest) statements require 0^0 = 1 as a convention.[20]
(引用終り)
以上

>>400 タイポ訂正

The consensus is to use the definition 0^0=1 0^0=1, although there are textbooks that refrain from defining 0^0."[19]
　↓
The consensus is to use the definition 0^0=1, although there are textbooks that refrain from defining 0^0."[19]

>>3
それ結構深い比喩かもとちょっと思った

>>20
いやいや背理法だよ

とんでも数学

●青戸六丁目被害者住民一同「色川高志の金属バット集団殴打撲殺を熱望します」
長木親父＆長木よしあき（盗聴盗撮犯罪者の色川高志を逮捕に追い込む会＆被害者の会会長）住所＝東京都葛飾区青戸6－23－20
●龍神連合五代目総長・色川高志（葛飾区青戸６－２３－２１ハイツニュー青戸１０３）の挑発
色川高志「糞関東連合文句があったらいつでも俺様を金属バットで殴り殺しに来やがれっ!! 糞関東連合の見立・石元・伊藤リオンの糞野郎どもは
龍神連合五代目総長の俺様がぶちのめしてやるぜっ!! 賞金をやるからいつでもかかって来いっ!!　糞バエ関東連合どもっ!! 待ってるぜっ!!」(挑戦状)

●青戸六丁目被害者住民一同「盗聴盗撮犯罪者の色川高志の逮捕を要請します」
長木親父＆長木よしあき（盗聴盗撮犯罪者の色川高志を逮捕に追い込む会＆被害者の会会長）住所＝東京都葛飾区青戸6－23－20
●盗聴盗撮つきまとい嫌がらせ犯罪者／アナル挿入食糞愛好家で生活保護費不正受給犯罪者の色川高志
色川高志の住所＝東京都葛飾区青戸６－２３－２１ハイツニュー青戸１０３号室
【通報先】亀有警察署＝東京都葛飾区新宿4ー22ー19　℡０３ー３６０７ー０１１０

盗聴盗撮つきまとい嫌がらせ犯罪者／アナル挿入食糞愛好家で生活保護費不正受給犯罪者である色川高志の盗聴盗撮つきまとい嫌がらせ犯罪者／愛人変態メス豚家畜清水婆婆（青戸6－23－19）の
五十路後半強制脱糞

アナル挿入食糞愛好家で生活保護費不正受給犯罪者の色川高志によりバスタブで清水婆婆の巨尻の肛門にシャワーのキャップをはずしてずっぽり挿入。
そして、大量浣腸。 勢い良く噴出！腸内洗浄状態です。

浣腸器と異なりどくどくと直腸内に注入され清水婆婆は激しくあえぎます

>>403
有理数と仮定して矛盾が起こるから有理数でないと結論するのは
厳密に言えば背理法ではなく
否定の定義
直観主義で排除しようとした背理法は
何々でないと仮定して矛盾が起こることから何々を結論すること

π+ｅとπｅのどちらかは超越数

どちらも代数的とすると(π+ｅ)^2も代数的、(π-ｅ)^2=(π+ｅ)^2-4πｅも代数的、これらの平方根であるπ+ｅ、π-ｅも代数的、よってπも代数的になりπの超越性に矛盾する。

これを背理法抜きで証明できる？

それも厳密には背理法ではない
超越数の定義が代数的ではないことだからだよ
代数的だとして矛盾が起こることが
代数的でないことの定義

それ間違ってる

>>407
背理法抜きで構成的に証明するのは遥かに難しい

>>409
間違いではないよ
直観主義論理の採用しなかつたこととは何かということと
否定の定義はなんとされているかを調べてごらん

>>410
恐らく無理じゃないかな
超越数の定義が代数的数ではないことで
代数的数であると仮定して矛盾することが定義だから
これも背理法だと思い込んでると
背理法は使わざるを得ないことになる

￢PとPから人が出る
すなわち
￢PからP→人が出て
P→人から￢Pが出る
というのは
直観主義論理より弱い最小論理でも採用してる公理

>>412
407は￢(AかつB)から(￢Aまたは￢B)を導いているから
直観主義論理では無効な議論だと思うけど

>>414
確かに

>>414
「a、bが超越数ならばa+bまたはabは超越数」の証明ならば背理法は不要
πやｅの超越性を前提にした上の話

>>416
背理法が不要というのは直観主義論理で
証明できるという意味？

>>407
Π+eとΠeのどちらかは超越数である。

まず、Π+e,とΠ-eのどちらかは超越数である。
何故ならば、Πは超越数かつΠ = {(Π+e)+(Π-e)}/2かつ代数的数全体は体なので。
Π+eが超越数とすると、「Π+eとΠeのどちらかは超越数である」は真。
Π-eが超越数とすると、(Π-e)^2 = (π+ｅ)^2-4πｅかつ代数的数全体は体であることより「Π+eとΠeのどちらかは超越数である」は真。
よってΠ+eとΠeのどちらかは超越数である。

開集合は直観論理だと何かに書いてあった

背理法でしかできない証明ってないの？

フェルマーの大定理？

>>420
解析学のいくつかの評価式については
背理法以外の証明は知られていない。

>>422
例えば？

背理法を他の同等の推論に置き換えるという意味だから
古典論理の否定ではないね

その程度の日本語も読めない馬鹿には数学は無理だから諦めろ

>>423
ヘルマンダーの有名な論文

>>425
どれ？
FOURIER INTEGRAL OPERATORS ってやつ？

とにかくActa Mathに出たやつ

Proposition 3.4.5

名著「非圧縮性粘性流の数学的理論」の第89ページの証明中、
「そうでなかったと仮定すると」で始まった文章が
「矛盾する」で終わっていない。
これは「見かけの背理法」か？

数学的帰納法不要論は？

>>430
bounded arithmeticという分野がその辺りを研究している

無矛盾であることが証明された系、または無矛盾であることが証明不可能であることが証明された系でしか背理法は使えないのでは？
矛盾を導出したとして、その原因が「仮定」にあるのか系自体にあるのか判別できないから

>>433
背理法は偽の命題を導いてその仮定が偽だとする論法
理論の無矛盾性なんて関係ない
つまり、もし偽の命題を導いてその仮定が偽であるかどうか知りたいならそれを証明の中で用いているか調べさえすればいい

中学生のときに以下のような妄想をした。

命題の論理をつなげて公理から定理、定理、定理とどんどん論理の網を
広げて行く際に、まるで複素関数論の解析接続のように、論理の網を
どんどんと進めていくときに、その経路によって結果に違いが出る
ことが起こらないのかなと。例えばｙ＝√ｘのような代数函数の
リーマン面は原点と無限円点以外では二価になっていて、そのことを
しらなければ、ｘ＝1のときｙ＝1から接続して原点の周りを回ってくると
ｘ＝1でｙ＝－1になるので、よって1＝－1だ、みたいな間違った結果を
導くけれども、それに類したことが起こらないのかという感じの妄想だ。
つまり、命題を証明する手段の網目をつなぐときの経路によって
異なる結果が得られても良いのではないだろうか、それは別のリーマン面の
シートに入り込んだようなものだと考えれば矛盾ではないと。
そういう妄想を抱いたのだ。

矛盾とは何を指すのかという妄想は湧かなかった？

>>434
矛盾が導出された理由が追加した仮定にあるのか系自体にあるのかが証明できないので仮定が偽である証明にはならない

延々とバグで紛れ込んだ裏面が続く悪夢的コンピューターゲーム。

排中律を証明できれば背理法を使ってもいいと思う。YESかNOか2択しかないっていう状況自体をまず証明してその上で背理法を使う。
これなら問題ないはず。

ある命題が「正しい」か「正しくない」か「決定不能」であるかの
3種類の"状態"があると思いますが、決定する手順が存在しないで
決定不能であっても、もしもたまたま成立することを示す例が
見付かれば「正しい」になるし、成立しないことを示す例が
見付かれば「正しくない」になるでしょう。

しかしたとえば、平面幾何で平行線公理を除いた体系を考えて、
その中で「平行線公理」を普通の命題のように考えて、
それが正しいか正しくないかを決定しようとしても、
正しいあるいは正しくないという証明はできないはずです。
つまりそのような「決定不能」の場合には、どれだけ成立例
あるいは反例をさがしたとしても、見付かるということは
あり得ませんね。

そうなると、正しいか、正しくないかの二通りだというのは
無理があるのではないでしょうか？　排中律は成り立つのでしょうか？

よく知らないけど直観主義論理はそういった違和感から産み出さたのかな？

ある程度複雑な体系はその中では真偽を決定出来ない命題が存在する、
とゲーデルがのたまっているそうだから排中律は成り立たないのではないだろうか？

決定できない命題を1つをとり、それを肯定するあるいは否定する命題を公理系に
新たに付け加えたとしても、その拡大された体系の中にも真偽を決定出来ない命題が
存在する，そこでその決定出来なかった命題をまた1つとり、それを肯定あるいは
否定する命題を再度公理系に新たに付け加えたとしても、その拡大された体系の
中には、。。。。。いくらやってもキリがないことになる。

　こんなことでは安心して夜も寝られない。それでも排中律は成り立つと言えるの？　

排中律は証明すべきものではないでしょう。
公理として認めてスタートするか、
認めないとするかを選べばいいだけ。
悩む時間があるなら、どっちかに決めて、
数学を始めた方が有意義。

決定不能な命題は真であると仮定しても偽であると仮定しても矛盾を導けないので気にする必要はない

＞こんなことでは安心して夜も寝られない。それでも排中律は成り立つと言えるの？
君は排中律の意味が全く理解できていない。
すでにコメントにあるが、決定不能な命題がその理論に存在しても排中律には何の影響も与えない。

理論Tに対して、その理論で決定不能な命題をAとする。
TからはAも￢Aもどちらも証明できないということは、
（1）TにAを加えたT+A
（2）Tに￢Aを加えたT+￢A
という二つの新しい理論が考えられ、そのどちらも矛盾しない。

しかし、排中律が成り立つということは（1）かつ（2）を考えると「Aかつ￢A」となって矛盾する。
ただこれだけのことだ。

長～い背理法ってウザい

基礎論バカはまじ不要

数学バカはもっと不要

>長～い背理法ってウザい
証明の長さに背理法か否かは全く関係がない．
長い証明はうざいかもしれないが，現状その証明しかないのならそれを理解するしかない．

>基礎論バカはまじ不要
>数学バカはもっと不要
確かにバカは不要かもしれんな．

しかし，基礎論や数学に通じている人間は総じてバカではない．
これは他の理学の研究者などでも同じこと．
だから，そんな人間はこの世にほぼいないだろうな．

最もこの世に必要ない連中は，何も学ばずに思い込みで何らかの分野をバカ呼ばわりする本物のバカだけだろう．

>ZFCなら排中律を証明できる
この事実だけなら確か1950年あたりには既に知られているはず．

直感主義論理で解析を実行しようという数学もあるけど，その場合の集合論では選択公理は入れてはいけない．
「Z＋選択公理」を集合論の前提にしてしまうと，論理が直観主義論理でも集合に関する全ての事柄で排中律が成り立ってしまうから，せっかく直観主義論理でやったら古典論理とどう違うのかを考えているのに，古典論理でやったのと区別がつかなくなる．
同じ理由で（普通の）正則性公理を仮定しても排中律が出る．

直観主義的集合論でも選択公理や正則性公理（基礎の公理）の名前は出てくるが，それは通常のZFCのそれらより弱い形のもので別物だ．

本物のバカは希少種

>>411
>直観主義論理の採用しなかつたこととは何かということと
自然演繹（推論）における「否定の導入」という推論規則が別名背理法なんだよ．
そして，背理法の原理はそのままこの否定の導入でもある．
演繹定理があるから否定の導入の推論規則は「公理」の形に書き換えることもできるから，やる意味はないが「対偶の公理」のように「背理法の公理」とすることもできる．

古典論理はこの「否定の導入」だけでなく「排中律」つまり実質は「二重否定の除去」に相当する否定の特徴づけが加えてある．
直観主義論理には否定に関しては「否定の導入」しかない．

理論Γと命題Aを仮定して，それがΓと矛盾する事を示して，¬Aを結論づける論法が背理法（否定の導入に対応）だ．

(1)．Γ,A ⊢ P(B,C,D,…）⇛⊥(矛盾)，よって¬A

対して，最初の仮定をAから¬Aに置き換えたものが

(2)．Γ,¬A ⊢ P(B,C,D,…）⇛⊥(矛盾)，よって¬(¬A)

となる．直観主義論理だと最後の¬(¬A)はAと同じと言い切れないが，古典論理ならおなじになる．

(2’)．Γ,¬A ⊢ P(B,C,D,…）⇛⊥(矛盾)，よってA

そして背理法とは，なんの断りもなければ，(1)，(2’)を自由に扱って良い古典論理の場合の事をさす．

>>452
希少だが，声がでかいからバカが目立つ．
数学や基礎論に親でも殺されたのかというぐらいにヘイトがあるから真正のバカはすぐ分かる．

声がデカいのはどう見ても基礎カスだろうが

スレ見渡したけど、クソスレだった．．．

>>455
基礎論（この場合は証明論）に関する話題で基礎論を排除しようという奴らこそがキチガイ。

料理教室で「料理の先生煩い」と吠えるDQN猿と一緒。

ブヒブヒブヒｗｗｗｗｗｗｗｗｗｗｗｗｗｗｗ

>>453
話の前後関係しらんけど

> 自然演繹（推論）における「否定の導入」という推論規則が別名背理法なんだよ

これは違うだろ
背理法は¬P→⊥からPを結論する
否定の導入はP→⊥から¬Pを結論する