【質問者必読!!】
まず>>1-4をよく読んでね
数学@5ch掲示板用 掲示板での数学記号の書き方例と一般的な記号の使用例
http://mathmathmath.dotera.net/
・まずは教科書、参考書、web検索などで調べるようにしましょう。(特に基本的な公式など)
・問題の写し間違いには気をつけましょう。
・長い分母分子を含む分数はきちんと括弧でくくりましょう。
(× x+1/x+2 ; ○((x+1)/(x+2)) )
・丸文字、顔文字、その他は環境やブラウザによりうまく表示できない場合があります。
どうしても画像を貼る場合はPCから直接見られるところに見やすい画像を貼ってください。
ピクトはPCから見られないことがあるので避けてください。
・質問者は名前を騙られたくない場合、トリップを付けましょう。
(トリップの付け方は 名前(N)に 俺!#oretrip ←適当なトリ)
・質問者は回答者がわかるように問題を書くようにしましょう。
でないと放置されることがあります。
(変に省略するより全文書いた方がいい、また説明なく習慣的でない記号を使わないように)
・質問者は何が分からないのか、どこまで考えたのかを明記しましょう。
それがない場合、放置されることがあります。
(特に、自分でやってみたのに合わないので教えてほしい、みたいなときは必ず書くように)
・回答者も節度ある回答を心がけてください。
・970くらいになったら次スレを立ててください。
※前スレ
高校数学の質問スレ Part420
http://2chb.net/r/math/1658820329/
高校数学の質問スレ Part421
http://2chb.net/r/math/1662638587/
高校数学の質問スレ Part422
http://2chb.net/r/math/1665137574/ 高校数学範囲で問題の意味が理解できる自作問題で
正解に自信がなくて質問するのもありです。
ここは高校数学スレなので高校の教科書にない言葉や解き方は禁止です
n番目の三角数とn+2番目の三角数が互いに素でないとき、最大公約数が3になることを証明せよ
累乗根の性質について、a>0, b>0で、m,n,pが正の整数のときに次のことが言えると、1から5まで性質が書いてあります。そのうち、3番目の次の性質について質問があります。(n_√a はaのn乗根を表すとします。a>0なので正の数一つになります。)
(n_√a)^m = n_√a^m
右辺n_√a^mの、a^mのmは正の整数である必要はないのではないかと思って反例を考えています。
n_√は、ルートの中が実数であれば、そのn乗根は正の数一つに決まります。だから、右辺n_√a^mの、a^mのmは実数でありさえすれば良いと思うのです。どうなのでしょうか。
よろしくお願いします。
>>5
それは、単に累乗根や累乗の世界で考えてるからn,mについて
正の整数という条件がついてるだけのことでしょ。
一般に、n,mが0以外の実数であれば(したがって、正負を問わず)
(a^(1/n))^m =(a^m)^(1/n)
は成り立つよ。反例なんか存在しない。 >>6
ここは作問のスレではなく、質問のスレなのでスレ違い。
出題はおやめください。 >>2
正解に自信がないのなら、それを提示して質問しないと駄目。
出題スレではないんだろ? >>7
レスありがとうございます。
単に、累乗根という制約の中での性質を表わすために、m,nが正の整数に限っているのだとしてもスッキリしません。
(n_√a)^m = n_√a^mの、√a^m部分でmが正の整数であることは累乗根には関係しないと思うからです。
次のように考えたのですが、どうでしょうか。
(n_√a)^m = n_√a^mの、右辺左辺は共に
a^(n/m)と表せます。
もし、1.1/2だとしても、nが11、mが20だとして考えれば良いです。そうすれば、m,nが正の整数という条件も満たします。 >>11
ありがとうございます。
結局、>>7さんの言う通り、
>n,mが0以外の実数であれば(したがって、正負を>問わず)
>(a^(1/n))^m =(a^m)^(1/n)
>は成り立つよ。
が正しくて、>>11さんの言う通り、累乗根の性質の所ではまだそこまで拡張されてないだけということなんだと理解しました。
チラっと、無理数乗も定義できるとかいてありました。高校では実数乗を含めて指数法則は習わないのかな? aを実数の定数とし、
f(x)=x^3+ax^2+x+1
g(x)=x^3+x^2+ax+1
とする。
(1)f(x)とg(x)がいずれも、極大値と極小値をもつようなaの条件を求めよ。
(2)(1)の条件下で、f(x)の極大値をM(a)、g(x)の極大値をN(a)とする。
M(a)とN(a)の大小を比較せよ。
>>12
m,n,pが正の整数のときに次のことが言える、というのは正の整数以外では成り立たない、という意味ではないですからね
教科書は何も間違ったことは書いてないですね >>7,12
あ、申し訳ない、もとの等式を読み違えてたわw
お察しの通り、累乗と累乗根という縛りがあるからm,nは正の整数
としてるだけの話にすぎない。
>>11が指摘してるように、指数を実数に拡張して定義すれば、
正の整数に限定しなくても成り立つことが言える(というか、
成り立つように拡張されている)。 >>12
実数乗の指数法則は高校数学(数II)で学んでるはず。
数IIの教科書をチェックしてみたが、まず累乗(指数が正整数のべき)しか
定義されてないことを前提として累乗根を定義している。
そのあとで指数の拡張として、指数が負の整数の場合と有理数の場合について、
指数法則を満たすように定義している。
さらに、指数が無理数の場合は、無理数を無限級数で表し、有限の項までで
打ち切った有理数のべきが近づいていく値としてぼんやり定義し、さらに証明
抜きで、それが指数法則を満たすとしている。 嫌がらせ目的の+1がすごく臭かったけど、やっぱりそういうことか
>>6
自答
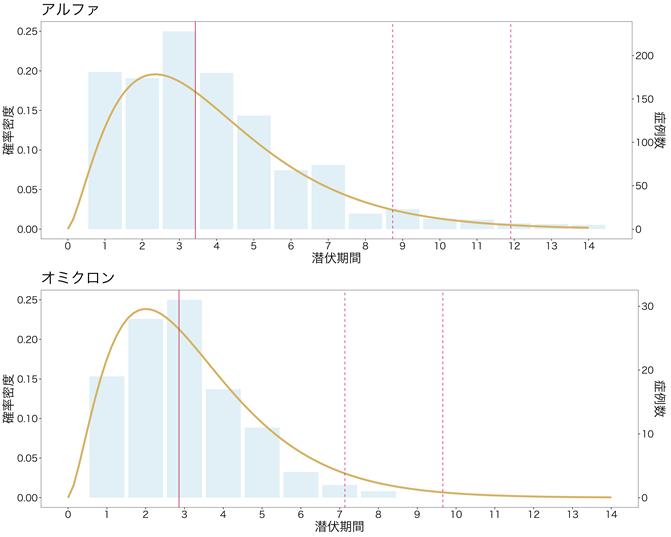
https://www.niid.go.jp/niid/ja/2019-ncov/2551-cepr/10903-b11529-period.html
35人の潜伏期は1,2,3,4,5日の人が各々2,8,15,9,1人である。
潜伏期の長さが既知の分布に従うという仮定を外して、
上記の頻度で潜伏期が分布すると仮定する(単位は日とする)。
子供が発症した翌日に親が発症したとして
親の方が子供の感染前日もしくはそれ以前の日に感染していた確率は29/245=0.1183673
親の方が子供の感染同日もしくはそれ以前の日に感染していた確率は17/49=0.3469388
潜伏期の長さを連続量として既知の分布に従うという仮定だと
対数正規分布、ガンマ分布、ワイブル分布で比較するとワイブルが理論確率と実測頻度の差(=残差)の平方和が最小
これを用いると親の方が先に感染していた確率は 0.2088579 と算出された。
潜伏期が1日未満とか5日超過とかもある確率で存在するはず(後者は無症状のスーパースプレッダーの存在で裏付けられる)。
臨床の答はひとつではない。
格言: 理屈と膏薬はどんなところにもつく 2つの箱A,Bと、50個の赤玉と50個の白玉がある。
これら100個の玉からランダムに50個を選んでAに入れ、残りの50個をBに入れた。AおよびBに各色の玉が何個ずつ入っているかは分からないものとする。
いまBから30個の玉を取り出したところ、赤玉がちょうど12個含まれていた。
この条件のもとでAに赤玉がちょうどk個含まれている確率をp(k)とするとき、
命題「k≠30ならばp(30)>p(k)」
の真偽を述べよ。
a(k)=Aに赤玉がk個ある条件の下でBから30個取ったら12個が赤玉である確率
=Bに50-k個の赤玉とk個の白玉があるとき30個取ったら12個が赤玉である確率
=C[50-k,12]C[k,18]/C[50,30]
b(k)=Aに赤玉がk個でありかつBから30個取ったら12個が赤玉である確率
=Aに赤玉がK個ある確率*a(k)=C[50,K]C[50,50-K]/C[100,50]*a(k)
=C[50,K]C[50,50-K]/C[100,50]*C[50-k,12]C[k,18]/C[50,30]
=50!/k!/(50-k)!*50!/(50-k)!/k!*(50-k)!/12!/(38-k)!*k!/18!/(k-18)!
/{100!/50!/50!*50!/30!/20!}
=50!/k!/(50-k)!/12!/(38-k)!/18!/(k-18)!/{100!/30!/20!}
=1/{k!(50-k)!(38-k)!(k-18)!}*50!/{100!30!20!18!12!}
Bから30個取ったら12個が赤玉である確率=Σ[k=18,38]b(k)
p(k)=b(k)/Σ[i=18,38]b(i)
p(30)/p(29)=b(30)/b(29)
={29!21!9!11!}/{30!20!8!12!}=1/30*21*9*1/12=189/360<1 ゆえに偽
f(x)=x^3+ax^2+x+1=(3x^2+2ax+1)(x/3+a/9)+(2/3-2a^2/9)x+1-a/9
g(x)=x^3+x^2+ax+1=(3x^2+2x+a)(x/3+1/9)+(2a/3-2/9)x+1-a/9
f'(x) 3x^2+2ax+1の判別式a^2-3が正→a<-√3または√3<a
g'(x) 3x^2+2x+aの判別式1-3aが正→1/3>a だから a<-√3
f(x)の極大を与えるxは(-a-√(a^2-3))/3だから
M(a)=(2/3-2a^2/9)*(-a-√(a^2-3))/3+1-a/9
g(x)の極大を与えるxは(-1-√(1-3a))/3だから
N(a)=(2a/3-2/9)*(-1-√(1-3a))/3+1-a/9
27(N(a)-M(a))=(6-2a^2)(-a-√(a^2-3))-(6a-2)(-1-√(1-3a))
=(-6a+2a^3)-2(3-a^2)√(a^2-3)+(6a-2)+2(3a-1)√(1-3a)
=2a^3-2+2(a^2-3)^(3/2)-2(1-3a)^(3/2)
<2a^3-2+2(a^2-0)^(3/2)-2(1-3a)^(3/2)
=-2-2(1-3a)^(3/2)<0 ゆえに N(a)<M(a)
>>19
5点を通る連続関数なんていくらでもあるけど選択の基準は? >>16
レスありがとうございます。
私の持っている数IIの教科書も、無理数の指数については、
おっしゃるように有理数の指数でその桁数を増やしていく級数を示す方法でした。
そして、実数乗についても指数法則を満たすということが「知られている」と締めくくられていました。
国公立の入試問題も実数乗の指数法則を使うようなものが出題されるということですね。
>>15 >>14
教科書は段階を踏んで解説しようとしているのはわかるのですが、
今扱っている制限内と全体との関係が示されないまま定理が示されるので、今回の誤解のように必要条件ではないのか誤解してしまいます。
ほかの参考書も、こういう誤解のないように示すものが皆無ではないかと思われます。 すみません、あとこれも教科書がらみのことなのですが、
3_√1の値を求めよという問題があります。
この正解は1でした。
y=x^3で、y=1のときのxの値のうち実数のものが1ということになります。
この解には虚数の値も考えられるので、1の三乗根は、実数と虚数(二個)の両方があります。
根号を使っているからと言って必ず実数であるというわけではないと思います。
たとえば、√-2は虚数です。
質問は、3_√1だけ示されていったいどうして実根だけを解答すればよいのかわかりません。
3_√1ってなんなのかと思ったら

これのことか
それはそういう定義だからってだけ
実数には1つだけ実数の三乗根があり、それをそう書く
だからそう書かれていたら「1の三乗根のうちの実数のもの」のこと
√(-2)は虚数だが、[3]√(-2)は実数だよ >>26
さっそくレスいただき、ありがとうございます。
>定義だからってだけ
>実数には1つだけ実数の三乗根があり、それをそう書く([3]√(-2)は実数)
y=x^3の実数のグラフの形状からイメージできました。
「1つだけ実数の三乗根があり」という部分で、すっきりした感じがします。
ありがとうございました。 >>24
>国公立の入試問題も実数乗の指数法則を使うようなものが出題される
もちろんです。
指数法則を満たすように指数が実数にまで拡張できているという前提に
立った上で、それに続いて実数を定義域とする指数関数やそのグラフを
扱ってるわけですから。対数関数しかりです。 >>25,27
累乗根と根号の関係は紛らわしくて、数学の本質とはあまり関係ないんだけど、
細かいところが気になる人は気になると思う。
高校数学の教科書をよくよく読むと、じつはそのあたりは破綻のないよう定義
されてて、以下のような感じになってる。
1)nが奇数のとき、実数aのn乗根のうち実数となるものがただ1つ存在するので、
それを_n√aと表す。たとえば、3√(-1) = -1
2)nが偶数のとき、「正の」実数aのn乗根のうち実数となるものは正、負2つ存在
するので、それぞれn√a と–n√a と表す。たとえば、4√1 = 1
負の実数aに対しては、実数となるn乗根は存在しない。
つまり、累乗根と根号は等価ではないことを認識する必要がある。「累乗根」は
複素数までその概念を自然に拡張できるが、「根号」は実数についてしか、教科書
には定義されていないので、複素数の世界にまで数を拡張した場合にも根号が表す
のは実数のみと考えてよいのであろう。
しかしながら、1),2)の定義ではnが偶数でaが負となる根号表現(たとえば、√(-2) )に
ついてはなにも言及されてない。そういう表現はダメとは書いてないのよね。
だから √(-1)=i と書くのがダメとは言い切れないから、混乱が生まれるような気がする。 >>29 の続き
こういう混乱が起きないようにするためには、複素数について学ぶ段階で、
根号の定義についてなにかしら言及しておいたほうが良いと思う。
数IIIの教科書を持ってないので、実際どうなってるか知らんけど。
まあ、曖昧にしておいたほうが良いという考え方もあるとは思うけどね。 a,b,pを実数の定数とする。3次方程式
x^3+ax^2+bx+p^3=0
が3重解を持つとき、a,b,pが満たす条件を求めよ。
>>21
Bから30個取ったところ12個が赤玉だった
→Bに含まれる赤玉は20個と推定される
→Aに含まれる赤玉は50-20=30個と推定される
→p(30)が最大
という予測はどこが間違っているのでしょうか >>13(1)
f(x)=x^3+ax^2+x+1
f'(x)=3x^2+2ax+1
f'(x)=0の2解α,βはα+β=-2a/3,αβ=1/3
f(α)-f(β)=α^3+aα^2+α+1-β^3-aβ^2-β-1>0
α^3-β^3+a(α^2-β^2)+α-β>0
α^2+αβ+β^2+a(α+β)<0
(α+β)^2-αβ+a(α+β)<0
(-2a/3)^2-(1/3)+a(-2a/3)<0
4a^2/9-1/3-2a^2/3<0
2a^2+3>0
任意のaが満たす。——(i)
g(x)=x^3+x^2+ax+1
g'(x)=3x^2+2x+a
g'(x)=0の2解γ,δはγ+δ=-2/3,γδ=a/3
g(γ)-g(δ)=γ^2+γδ+δ^2+γ+δ+a<0
(γ+δ)^2-γδ+γ+δ+a>0
(-2/3)^2-a/3-2/3+a>0
2a/3-2/9>0
6a-2>0
a>1/3——(ii)
(i)(ii)より ∴a>1/3 前>>33
>>13(2)
f(α)-g(γ)>0ならM(a)>N(a)
f(α)-g(γ)<0ならM(a)<N(a)
αは3x^2+2ax+1=0を解いて、
α=-{a+√(a^2-3)}/3
γは3x^2+2x+a=0を解いて、
γ=-{1+√(1-3a)}/3
M(a)-N(a)=f(α)-g(γ) >>32
最後のステップかな
確率分布が歪んでる場合は期待値と確率が最大となる値がズレるから
x^3+ax^2+bx+p^3=(x-t)^3=x^3-3x^2t+3xt^2-t^3
t=-pだからa=3p b=3p^2 >>4
pを素数とする n(n-1)/2がpの倍数↔n(n-1)が2pの倍数
↔①n=2p または②n-1=2p または③n=pかつn-1=2
①のとき (n+2)(n+1)/2=(2p+2)(2p+1)/2=(p+1)(2p+1)=pの倍数+1
②のとき (n+2)(n+1)/2=(2p+3)(2p+2)/2=(p+1)(2p+3)=pの倍数+3
③のとき n=p=3だから (n+2)(n+1)/2=5*4/2=10=pの倍数+1
①と③の場合はpの倍数ではないので共通の素因数を持たず互いに素である
②の場合はp=3の場合に3の倍数になるので3は共通因数になりえる
n(n-1)/2が9の倍数↔n(n-1)が18の倍数↔n,n-1が18,1か9*2か6*3のどれか↔偽
共通因数は9の倍数ではないので互いに素でないなら最大公約数は3 >>4
pを素数、mを整数とする n(n-1)/2=がpの倍数↔n(n-1)が2pの倍数
↔nがpの偶数倍または奇数倍 またはn-1がpの偶数倍または奇数倍
↔①n=2mp ②n=(2m+1)p ③n-1=2mp ④n-1=(2m+1)p
①のとき (n+2)(n+1)/2=(2mp+2)(2mp+1)/2=(mp+1)(2mp+1)=p*整数+1
②のとき (n+2)(n+1)/2=((2m+1)p+2)((2m+1)p+1)/2
=(p{(2m+1)^2p+3(2m+1)}+2)/2=p*(奇数+奇数)/2+1=p*整数+1
③のとき (n+2)(n+1)/2=(2mp+3)(2mp+2)/2=(2mp+3)(mp+1)=pの倍数+3
④のとき (n+2)(n+1)/2=((2m+1)p+3)((2m+1)p+2)/2
=(p{(2m+1)^2p+5(2m+1)}+6)/2=p*(奇数+奇数)/2+3=p*整数+3
①または②のときpの倍数にならず③または④のときp=3以外ではpの倍数にならない
n(n-1)/2=3^kのときn(n-1)=2*3^k
n,n-1は 2*3^k,1 3^k,2 2*3^(k-1),3 3^(k-1),2*3 2*3^(k-2),3^2・・・
のどれかだが差が小さい組は k=2a+1のとき3*3^aと2*3^a
k=2aのときで2*3^aと3^a どちらにせよ差は3^aでこれが1になるのはa=0のみ
kが正なら1しかないので互いに素でないなら最大公約数は3 ((n-1)n/2, (n+1)(n+2))
=(n(n-1)/2, 2n+1) [右-左]
=(4n(n-1), 2n+1) [右は奇数:左x2^3]
=((2n+1)(2n-3)+3, 2n+1) [nの多項式と思って左÷右]
=(3,2n+1) [左-右x(2n-3)]
=3 or 1
>>38
イナさん、コテハンやめたの?w
毎度、毎度せいがでるねぇwww lim[n→∞] ∫[0,2π] |sin(nx)|/(1+x^2) dx
を求めよ。
(√3)^(√3)^(√3)^…
は発散することを示せ。
2^n-2=(n-1)mが成り立つのは
n=8のときだけでしょうか?
>>44
凡庸な自作問題に的はずれな迷回答をするのはイナさんくらいのものかと思ったが、違うの? >>49
違いますよ
回答したレスに同じ質問するってどんな低脳だよ a[1]=1,b[1]=2,c[1]=3
t=1,2,...に対して
a[t+1]=ta[t]+b[t]+c[t]
b[t+1]=a[t]+tb[t]+c[t]
c[t+1]=a[t]+b[t]+tc[t]
上記を満たす数列a[t],b[t],c[t]の一般項を求めよ。
>>49
凡庸かどうかに関わらず、高校数学の範囲の質問にはすべて回答するのがこのスレの主旨です
自作問題や出題などもスレ違いではありません
ご理解よろしくお願いいたします aを実数とする。
f(x)=a/(1+x^2)が以下の条件をすべて満たすという。
・lim[t→∞] ∫[-t,t] f(x) dx = 1
・任意の実数xに対して0≦f(x)≦1
(1)aを求めよ。
(2)任意の実数sに対して、∫[s,g(s)] f(x) dx = 1/3を満たす実数g(s)がただ1つ存在することを示せ。
(3)lim[s→∞] g(s)/s を求めよ。
>>20
kがどんな分布をするのか興味がわいたので
二項分布と超幾何分布の関数をプログラミングして描画。

ソフトウェアを使って描画できる素養のある人の検証を希望。
んで、こんな問題を考えてみた。
改題
2つの箱A,Bと、50個の赤玉と50個の白玉がある。
これら100個の玉からランダムに50個を選んでAに入れ、残りの50個をBに入れた。AおよびBに各色の玉が何個ずつ入っているかは分からないものとする。
いまBから30個の玉を取り出したところ、赤玉がちょうど12個含まれていた。
この条件のもとでAに含まれる赤玉の数の期待値を求めよ。答は四捨五入した整数でよい。
俺の答は28 >>32
p(28)が最大じゃないかな?
二項分布と超幾何分布に条件付き確率を組み合わせた複雑な問題だと思う。 >>52
同意。
問題の意味が高校数学で理解できないようなのはスレ違いだと思うが、それ以外は許容されるべき。
例えば、小中学算数スレに四色問題を出してもいいと思う。
解法に高度な定理(例パップスギュルダン)を使おうがプログラムで近似解を出そうが構わんと思う。
自分の趣味に合わないならスルーすればいいだけ。 フェルマーの小定理はもちろん、大定理に関する話題もこのスレの対象です
>>54
検算に乱数発生させてシミュレーションしたら27になった。

オマケ Rのコード
sim=\(){
b=sum(sample(c(rep(1,50),rep(0,50)),50))
B=c(rep(1,b),rep(0,50-b))
flg<-sum(sample(B,30))==12
while(!flg){
b=sum(sample(c(rep(1,50),rep(0,50)),50))
B=c(rep(1,b),rep(0,50-b))
flg<-sum(sample(B,30))==12
}
50-b
}
y=replicate(1e5,sim())
hist(y)
summary(y) 臨床問題wに改変
2つのシリツ医大(裏口医大と底辺医大)にどちらも50人の推薦枠がある。
合計で裏口入学が50人正規入学が50人入学した。
裏口医大の推薦枠の学生を30人抽出して調査したところ12人が裏口であった。
底辺医大の推薦枠50人のうちの裏口入学の数の期待値を求めよ。
>>50
君とイナさんが同じレベルだって言ってんだよ。
皮肉もわからん低能かw >>56
出題への解答と、質問への回答は別のジャンルだろ。
そんなこともわからないバカがなにをほざいても虚しいだけだよw 高校数学の出題スレでも作りゃいいじゃん。
なんで質問スレでわざわざ自作問題を出題してんの?
頭悪いの?
ポエムクリエイターはどういうわけかポエムスレを避けます
前>>47
>>54
俺の答えは30個。
∵Bに30個中12個の赤玉が入っているということは、
50個中12×(50/30)=20(個)の赤玉が入っている可能性が高い。
50-20=30 >>60
人の回答笑うとかいい趣味してるなチンカス
早く死ねやバーカ >>63
あなた分かってないですねえ
私が行っているのは質問です
出題は行っておりません
ちなみに私は出題を認めません、ここは質問スレですので >>63
キチガイを通報して書き込み禁止にさせろよ。それ以外に有効な手段はない。それが出来ないなら黙っているしかない。多分出来ないだろうけどな。お前の負けだよ。 >>63
要するにお前の敵は
掲示板の管理者
キチガイを相手にする回答者
キチガイを黙認する第三者
の全てだ。
大局的に見ればお前の書き込みはキチガイを活気づかせる燃料になっているに過ぎない。キチガイをこのスレから追い出すことは恐らく出来ない。 >>67
君がやってるのは質問ではなく、出題以外の何物でもないことを認めるべきだな。
そうでないと君の精神疾患は死ぬまで治らない。 >>69
確かに、あなたは活気づいているようですね。
それはそれで致し方ないと思ってます。
あなたの燃料になろうがなるまいが、正論を提起し続けないとね。 >>64
>ポエムクリエイターはどういうわけかポエムスレを避けます
面白い指摘ですね。>>67さん、読みましたか? >>70
だから質問してるだけですって
問題は別から持ってきています >>66
イナさんのほうが人柄は百倍よさそうだねw
いっしょくたにしてごめんね >イナさん >>73
ならば、問題の出典を明らかにすべきでしょうね。 このまま雑談が続くのは良くないので質問の流れに戻しますね
f(t) = ∫[0,1] (1+tx)/(1+tx^2) dx
とする。
tがすべての実数を動くとき、f(t)の増減を調べよ。
>>71
正論などない。お前が浮いているだけ。そして今回もお前の負け。
お前の書き込みでは何も変わることはない。むしろお前の方がキチガイよりもうざく感じられてお前の擁護者がいなくなった。 >>74
この馬鹿は一貫してイナを擁護している。それが矛盾を生じてキチガイを追い出す主張が一貫性を欠くことになっている。 >>70
死ぬまで治らないと結論したということは、お前が自分の負け(=キチガイが出ていかないこと)を認めたことになる。 f(t) = ∫[0,1] (1+tx)/(1+tx^2) dx
とする。
tがすべての実数を動くとき、f(t)の増減を調べよ。
>>78
擁護など必要ありませんが、あなたはいったい何がしたいの?
それこそスルーすれば良いだけなのでは? >>77
出典が書いてないとはこれいかに?
では、その問題は何を参照して書いたの? >>80
管理人でもない限り、誰もスレから追い出すことなどできませんよ。
ただ正論を唱えることで、書き込みをしている人の良心に訴え、
スレを読んでいる第三者に同意を求めているだけ。 >>80
>一貫してイナを擁護している。
イナさんはあなたと同列だと言ってるのだから、擁護しているわけないでしょ。
ただ、コテハンで書いているところなどはまだしも良心的だとは思ってますよ。
専ブラでNGするのは簡単ですから。実際、私はそうしてます。 >>85
ちなみに82も出典がありませんが名作だと考えております >>86
無駄だ。
そのうち馬鹿なお前にもそのことが理解出来る日がくるかもしれない。 このスレの中で、キチガイと追い出し工作人のどちらが勝つか見てみるとするか。
俺はこのスレでもキチガイが勝つと予想する。
>>88
その本はなんなの?それが出典になるでしょ。 >>89
解法もわからんのに名作かどうかなんてわからんでしょ?
どうかしてるんじゃないの? >>90
はなから無駄な努力だと分かってやってるんですよ。 >>91
追い出し工作なんてしてませんよ。
したがって、勝ち負けなんてありません。
このスレを読む第三者に、どちらの言い分が正しいか各自が
判断してもらえればいいだけです。
できれば、おそらくスレ立てをしたであろう出題マニアが
改心してくれればいいのですが、それは期待できないでしょうね。 追い出し工作なんてしてませんよ。
↓
このスレを読む第三者に、どちらの言い分が正しいか各自が
判断してもらえればいいだけです。
馬鹿だな。「工作人の書き込みの無いスレ」を見て自分で判断するのならばそれで良いが
「工作人の書き込みを見て判断してもらう」というのは工作そのものだ。
馬鹿にはわからないのだろうな。
そして結果はキチガイの勝ち。
>>48
パスカルの三角形の上から偶数段目の底辺側の総和を見ているとそんな気がするけど、n≦8までの偶数でしか成り立たないよね >>46>>99
成り立つって整数mが存在するってことなら
n=8のとき成り立たないし
n=0,1,2,3,7,19,43,...と成り立つのはたくさんあるが 素数のときその素数の倍数になってるって話か
1,11,55,165,330,462,462,330,165,55,11,1
1,13,78,286,715,1287,1716,1716,1287,715,286,78,13,1
1,17,136,680,2380,6188,12376,19448,24310,24310,19448,12376,6188,2380,680,136,17,1
1,19,171,969,3876,11628,27132,50388,75582,92378,92378,75582,50388,27132,11628,3876,969,171,19,1
2^n-2=nmが成り立つので素数じゃないのはフェルマー擬素数
3^n=k^2-p…(*)
を満たす正整数の組(n,k,p)を考える。
(1)p=40のとき、(*)を満たす(n,k)をすべて求めよ。
(2)p=41のとき、(*)を満たす(n,k)は存在するか。
>>96
工作人ってどういうこと?
追い出し工作というのは、管理人対してに何らかの要請をすること以外にはないのでは?
理解に苦しみますねぇ。
あなた、思い込みが強すぎるのでは?異常なレベルだと思いますよ。 >>105
あのお…
1日で18レスは異常なレベルだと思いますけど… 書き込み数の多寡なんて別にどうでもいいんじゃないの?
気になる?
>>105
工作とは
ある目的のために、計画的な働きかけを行うこと。
キチガイの追い出しに関して工作を行っている人間ということ。
こいつ頭悪すぎ… >>107
書き込みの回数が多い=執念深い。
まさしく「追い出し工作」を諮る人間に相応しい行動。 次の極限が存在するならその値とそうなる理由を、存在しないならその理由を答えよ。

これもお願いします。

昔名古屋の地下鉄は、
どの2駅間も高々1回の乗換で行けるといってました(今は知りませんが)
これはどの2つの路線も少なくとも1つの乗換駅をもつということでしょうか。
>>109
だから追い出そうとなんかしてないんだってば。
バカな出題をやめてくれってだけのこと。 昔は十字型の2路線しかなかったんです
なので当然「どの2つの路線も少なくとも1つの乗換駅をもつ」ことにはなります
>>110
やっぱ、頭おかしいわ、君w
何度言ってもわからんのじゃ処置なし。 >>111,112
なにがしたいの?
高校数学じゃないでしょ。
どこから引っ張り出したのそんなもの? >>114
↓
>>63
>>116
頭悪いな。書き込み回数に関してごまかそうとしてもそれは無理。
お前が自分の置かれている状況が分からない馬鹿であり、以後もキチガイ追い出し工作が続くことがはっきりした。 >>118
分岐した別路線で電車が相互乗り入れしてればその限りではないな。 >>119
出題は別スレでやれ、ってことと、ここに書き込みするなってのはイコールじゃないよ。
そんなこともわからんとは、やっぱ頭おかしいわ、君w >>122
分からないから尋ねてるんだよ。
君はどこから引っ張り出したのか知ってるのかね? >>123
ことごとく論破されて悔しい気持ちはわからんでもないが、
不毛だからもうやめとけ。もっとハゲるぞw >>126
俺は全く論破されていない。
お前の方が完全論破され続けているだけ。
スレが進むに連れてより一層惨めな姿を晒すのはお前の方だから見てろよ。誰の目にも明らかになる。
>高校数学の範疇といえなくもない。
ここでも矛盾が生じている。馬鹿の一つ覚えの「出 典」はどうした? >>121
この馬鹿はキチガイ本人が「質問をしているという認識」であって、「この馬鹿の区分に従うつもりが無い」という前提を無視している。
俺は「そここそが論点」なのであり、「出題をしないで単なる質問だけするキチガイならば容認する=追い出さない」というこの馬鹿の区分は無意味だと考えている。 >>129(キチガイのアイデンティティは出題にあるということ)が前提になっていない時点で、追い出し工作をはかっている馬鹿は「相当下層の馬鹿」であると俺は考える。 >>128
出題じゃないんだから出典もクソもないだろ。
また論破されちゃったね、君w >>129
なに騙されてんの?w
彼が出題を質問だと認識してるわけじゃなくて、単なる言い訳けなのはミエミエ。
だから悪質なんだよ。 >>130
ID変えるってどういうこと?俺はそんな姑息なことしてないよ。 >>133
またこの馬鹿が馬鹿を晒したな。
「この路線の問題は高校数学ではない」のであえて俺は「出 典」と言っているのだ。
高校数学の範囲でこの路線の問題に答えられるのならば答えててみろよ馬鹿。 >>131
あんたがどういうキチガイじみた考えを持とうが勝手だが、
追い出し工作をはかってる人間などいないよ。
妄想をめぐらしてる時点であんたのほうがキチガイにしか見えん。 >>137
複数の線分が交差していて、線分上の任意の点から別の点へ移動するのに、
たかだか1回だけ向きを変えれば到達できるとすれば、任意の2つの線分
は必ず共有点を持つことを証明せよ。
これなら背理法で証明できるだろ。 >>140
ごまかさないで高校範囲で完全解答と思われる解答を作ってからレスしろよ。
完全論破してやるよ笑 >>132
けしからんバカですか 了解
高校数学の範囲で答えろという出題に答えた人もけしからんバカなんですかね? 碁盤目の線と線の交点を駅にして縦線は全部独立した路線、横線ははじのところで次のだんにくっつけて長大な蛇行してる路線一本に繋げてしまえばどの2駅間も乗り換えなしで、縦の路線通しはひとつも乗り換え不可能の状況になる
>>58
シミュレーション結果と一致しなかったので、再検討したら立式の間違いを見つけたので再計算
p(k)の分布(青がシミュレーション、●が理論値)
 は
は
最頻値は27
期待値は27.13394
になった。 >>144
二項分布は関係なかったな。超幾何分布とベイズの公式を使って立式すればよいことに気づいた。
シミュレーションにも同じミスがあったので修正。

>>65
ベイズの公式を使うだけ
Ak:Aの箱に赤玉がk個ある事象
!Ak:その余事象
B12:Bの箱の30個のうち12個が赤玉の事象
P[Ak|B12]=P[B12|Ak]*P[Ak]/( P[B12|Ak]*P[Ak]+P[B12|!Ak]*P[!Ak] ) >>141
なにもごまかしてなどいないけど?
解答は簡単でしょ。
対偶を証明すればいい。
出発点Aが線分をa上に,終着点Bが異なる線分b上にあるとする。
aとbが共有点を持たなければ、AからBに至るまでに別の線分
を経由しなければ到達できない。経由する線分とaとの経路上
の交点をPとし、bとの経路上の交点をQとすれば、P≠Q(
P=Qであれば、P=Qはaとbの共有点になるので前提と矛盾)。
よって、AからBにたどり着くためには少なくともP,Qの2点で
向きを変えなければならない。 >>142
>高校数学の範囲で答えろという出題に答えた人もけしからんバカなんですかね?
ん?それって >>39のことでしょ? n≧3とする。
n個の箱にn個の玉を1つずつ無作為に投げ入れる。
入っている玉の個数が最も多い箱と最も少ない箱について、その玉の個数の差をk
とする。
k=3となる確率をnで表せ。
ここは質問をするスレです
回答をするスレではありません
>>145
元の問題>20に返って
命題「k≠30ならばp(30)>p(k)」
の対偶
「p(30)<=p(k)ならばk=30」
で考える
その不等式が成り立つkを求めると
> k[p(30)<=p(k)]
[1] 25 26 27 28 29 30
なので偽とわかる。 >>150
改題
n≧3とする。
n個の箱にn個の玉を1つずつ無作為に投げ入れる。
入っている玉の個数が最も多い箱と最も少ない箱について、その玉の個数の差をk
とする。
k=3となる確率が最も大きいnを求めよ >>154
なにそれ?w
基本的に>>113の質問に対する回答の補足なんだから全然いいでしょ。
>>137を出題というのは語弊がある。ってか、どうかしてる。 >>150
すいません
この質問に答えていただきたいのですが…
皆さん、スレの本来の目的を思い出してください この路線の問題に答えよって言ってるんだから出題だよ
>>157
>スレの本来の目的
高校数学に関する質問とそれに対する回答をすることであって、
出題したり、それに解答したりすることではない。 >>159
そういうのをアスペルガー的な解釈って言うんだよ。 >>161
言わないよ
>>137が分からないから教えてくださいって質問ではないことは明らか
レッキとした出題だよ >>158
あの、150は質問なんですけど…
質問ではなく出題だと仰るなら
・質問でないという根拠
・出題であるという根拠
の2点を示してください >>162
だって、>>137単体では問題にすらなってないんだがw
強弁はやめとけ。見苦しいだけだから。 >>165
見ての通り、>>140なら問題の形式になってるが、>>137はそうではない。
質問内容をあえて問題形式にしただけなので、もちろん出題ではないしな。 >>163
質問というのは、疑問点やわからない点を問いただすことだが、>>150はそうなっていない。
出題というのは試験で解くような問題を提示することで、まさに>>150はその形式に則っている。
これが客観的な解答だよ。 >>169
ありがとうございます
ではこれなら、あなたも質問と認めますね
win-winです
n≧3とする。
n個の箱にn個の玉を1つずつ無作為に投げ入れる。
入っている玉の個数が最も多い箱と最も少ない箱について、その玉の個数の差をk
とする。
k=3となる確率をnで表せ。
…という問題が分かりません。どう手を付けていいかも分かりません。教えてください。 >>28
>>30
レスが遅くなり申し訳ありません。
ご丁寧なレスをいただきまして、ありがとうございます。
定義というものをもっとしっかり意識して、自分の立っているところを自覚できるように心がけたいと思います。 >>167
この馬鹿は何を自分でやっているかわからなくなってるのか?
>>113(=高校範囲ではない問い)
に対するレス>>118に関して俺は問い質している。はぐらかそうとしても無理。
それに加えて
「>>140(お前の自作問題)は何なのか、>>113ののことなのか」の説明を求める。そもそも140と113は違う問題なので。 高校範囲外の質問をする奴Aとそれに回答する奴Bとの関係は
出題をする奴Cとそれに回答する奴Dとの関係に等しい。
B=キチガイ追い出し工作人
C=キチガイ、およびキチガイ追い出し工作人
前>>65
>>170
n≧3だからたとえばn=5とすると、
5個の箱に🎁🎁🎁🎁🎁
5個の球を⚾⚾⚾⚾⚾
入れ、k=3となるのは、
🎁🥎🥎🥎
🎁🥎
🎁🥎
🎁
🎁
または、
🎁🥎🥎🥎
🎁🥎🥎
🎁
🎁
🎁
のどっちかのパターンしかない。
球の色は変わったけど関係ない。
確率を計算すると、
0,0,1,1,3→5×(4C2)=5×4×3=60
0,0,0,2,3→5×4=20
(20+60)/5^5=80/(625×5)=16/625=2^4/5^4=(2/5)^4
=(2/5)^(n-1)
={(n-3)/n}^(n-1)
∴k=3となる確率は{(n-3)/n}^(n-1) 前>>175
n=5の場合から推定しただけなんで違う可能性がある。 >>166
だから何?単体云々の話など誰もしてないんだが?
もん‐だい【問題】 の解説
1 解答を求める問い。
なのだから問題になってるよ
他のレスを前提にしてるかしてないかなど関係ない >>170
もう駄目だよ。
いったん出題したものを、質問に見せかけても手遅れだよ。
残念でした。 >>177
>>137を出題というのは無理があることくらいバカでもわかるだろ。
あのレス単体が試験に出て答えられるか?
あんた必死すぎて気の毒になってくるわw >>171
どういたしまして。
スレ違いのおかしな投稿が多い中、あなたの真摯な質問は一服の清涼剤でした。 >>178
では別の質問をします
これで大丈夫ですね
n≧4とする。
n個の箱にn個の玉を1つずつ無作為に投げ入れる。
入っている玉の個数が最も多い箱と最も少ない箱について、その玉の個数の差をk
とする。
k=3となる確率をnで表せ。
…という問題が分かりません。どう手を付けていいかも分かりません。教えてください。 >>179
そうだね スレの流れを無視して単体で試験に出されても答えられるわけ無いね
だから何だね? スレの流れがある5chとそれがない試験が同列になるわけないじゃん
>>181
出題を質問形式にしてるだけだから駄目だな。
努力のあとも見せずに、出題された問題をまるまる解けとだけ言ってるのも論外。 >>185
あなたの言う質問の条件を満たしています
なのに出題だと強弁するんですね
まったく、あなた自身の愚かさを噛み締めなさい >>187
非難しているのがあなただけなのは草でございます >>185
ではさらに別の質問をします
これで大丈夫ですね
n≧5とする。
n個の箱にn個の玉を1つずつ無作為に投げ入れる。
入っている玉の個数が最も多い箱と最も少ない箱について、その玉の個数の差をk
とする。
k=3となる確率をnで表せ。
…という問題が分かりません。どう手を付けていいかも分かりません。教えてください。 >>186
スレの流れを無視して単体で試験として抜き出せばという前提の話でしかないな
>>187
それ自体で完結してるものもあればそうでないものもあるってだけでしかないな キチガイ追い出し工作人は自分自身問題を出題しているのと、高校範囲外(=スレ違い)の質問に回答しているので、他人に文句を言う資格は無い。
一番の荒らしはキチガイ追い出し工作人てある。現在彼は完全に劣勢になっている。
ところで>>140→>>141はどうした? >>181
キチガイが出題を質問に変えたか笑
これは間違いなく質問だ。
「この形式ならば」日本中どこに行っても質問という日本語の指し示す内容に合致する。 キチガイがスレに適応して「普通の人」になったことで、この人がこの形式を続ける限りにおいて批判される筋合いがなくなった。
彼の行為に対してわめき散らしていた「一番の荒らし」が今後大人しく引っ込むのかそれとも荒らし行為を続けるのか興味がある。
>>42
(2n^4+1)/(n^2+1) = 2(n^2-1) + 3/(n^2+1) = m
を満たす整数 m が存在しないので互いに素。
>>45
(√3)^x = x
を満たす実数 x が存在しないので発散。 出題者はシミュレーション解のネタを提供してくれてありがたい。
一般解の問題はシミュレーションで解決し難いのでスルーしている。
>>65
Bの箱に全部で赤玉20個入っているときは、
Bの箱から30個取り出したときの赤玉の数が12個の確率が最大だといえるけど、
30個取り出して12個赤だったときにBの箱に全部で赤玉が何個入っている確率が最大かを計算すると20個にはならんと思う。 >>190
わざわざ質問形式にしなくていいから、数値解を求める出題をお願いします。 改題
2つの箱A,Bと、50個の赤玉と50個の白玉がある。
これら100個の玉からランダムに50個を選んでAに入れ、残りの50個をBに入れた。AおよびBに各色の玉が何個ずつ入っているかは分からないものとする。
いまBから30個の玉を取り出したところ、赤玉がちょうど12個含まれていた。
(1)Bに全部で25個以上の赤玉が入っている確率を求めよ。
(2)Bに含まれる赤玉の数として最も確率が大きいのはいくつか?
(3)Bに含まれる赤玉の数の期待値を求めよ(小数第三位までの近似値でよい)。
>>189
いや、俺だけでなく君をキチガイ呼ばわりしている>>192も暗に非難してるんだよ。
なぜか彼は俺にも噛み付いてるけどねw
君をキチガイだとは思わんが、いわゆる人格障害なのは間違いないはず。
おそらく普段の生活でも周囲と軋轢を起こして苦労してるんだろうね。 >>192
おいおい、スレをよく読み返せよ。
頭に血が昇って見落とししてるぞw
しかし、出題キチガイを利するような書き込みをするようじゃどうしようもないな。
情けないやつだ。 出題された問題を解けない輩が基地外扱いしているだけだろうな。
医師スレでもシリツ医=裏口容疑者が同様の行動をしている。
底辺シリツ医って自分が知らないこという人は統合失調症認定。
そんな低能だから国立大学に合格できないのだと思う。
当直医のスレ Part 31
http://2chb.net/r/hosp/1651363181/819
819 名前:卵の名無しさん[sage] 投稿日:2022/12/06(火) 13:17:31.11 ID:LOe/VzyA
>>816
エアウェイスコープがマックグラスに勝ってるとこってどこだよwww
使ったことない癖に医者のフリするなよ尿瓶ジジイwww
824 名前:卵の名無しさん[sage] 投稿日:2022/12/07(水) 21:38:59.27 ID:5JO5B4ih
>>819
座位でも対面でも使える。
827 名前:卵の名無しさん[sage] 投稿日:2022/12/08(木) 07:36:35.32 ID:MY5n2WI5
>>824
???何言ってんのお前
座位、対面で挿管?どういう場面だよ
っていうか、やっぱりお前統合失調症だろ
980 名前:卵の名無しさん[sage] 投稿日:2022/12/25(日) 06:43:15.93 ID:MJIMDXwJ [1/3]
>>827
AWSのプロモーションビデオすらみたことない情弱かよ。
982 名前:卵の名無しさん[sage] 投稿日:2022/12/25(日) 07:10:01.50 ID:MJIMDXwJ [3/3]
知らないなら検索すれば
こういうのが簡単にみつかるのに
対面坐位におけるエアウェイスコープ,エアトラックの使用経験-気管支ファイバー挿管の代用としての可能性-
ほんと裏口容疑者って無能だな。
まあそれ故に国立大学に入れる学力がつかなかったわけだが。 このスレが潰れたら質問に来た奴が板全体に広がるよ
あと問題が間違っているから解けるわけない
>>205
仕事の時間以外はネット三昧なんですか?
もしかして独身? 他スレのやり取りなんて誰も興味ないから貼るなつったろ
>>208
いや、嫁と一緒にピザやパンを焼いたり、低温調理や圧力鍋で料理をしてしている。
クリスマスのチキンも二人でで調理した。
今はフランスパンの二次発酵中。
Youtubeに料理動画があっていろいろ楽しめる。
理詰めで料理したい人にお勧めはこれ!
「Cooking for Geeks 第2版 ―料理の科学と実践レシピ」 >>209
ところがだ、医師が羨ましくて医師板に出張して荒らしている椰子がいるんだよ。
臨床医じゃないから、統失認定できないらしくてチンパンジー認定が得意技のようだ。
医師が羨ましければ再受験でもすればいいのにと助言してやっているんだが。
俺の同期は2~3割は学卒だったな。大半は東大卒か京大卒。
当時は阪大医学部には学卒入学制度があったから阪大卒はいなかったな。
歯学部には東大数学科卒もいた。 >>175
箱の中の玉の数の最大値が3のときにk=3になるようなので
分数で厳密解を出せるように指折り数える(プログラムを作って動かしてみると
> calc(3)
[1] 1/9
> calc(4)
[1] 3/16
> calc(5)
[1] 32/125
> calc(6)
[1] 1225/3888
> calc(7)
[1] 685/1872
一般解は賢人にお任せ。 >>212
チンパンジー認定厨本人にシリツ卒なのか?と聞いても答えずに逃亡するんだよなぁ。 >>206
問題が条件不足で答が出せないなら、自分で条件を補えばいいだけ。
例えば、
ゴルゴ13は100発100中
ゴルゴ14は10発10中
ゴルゴ15は1発1中
とする。
各々10000発撃ったとき各ゴルゴの命中数の期待値はいくらか?
これだけでは答がだせないが、
各ゴルゴの狙撃成功確率の事前分布は一様分布とする
という条件をつければ期待値が計算できる。 >216の問題の意味は小学生にもわかるだろうな。
期待値の厳密な定義といいだすと無理だけど
命中率10割でもゴルゴ13,14,15の順に当たる数が減るだろうというのは予想できるけど、
どれくらい違うんだろうというのは興味が湧くはず。
β分布を小学生にわかるように説明できる自信は俺にはないけど。
興味ない問題はスルー。
これができない椰子が多いよね。
出題フェチは俺に興味深い問題を投稿してくれるから感謝している。
興味ない問題はスルーすればいいだけ。
面白そうな問題は改変して楽しめるし。
確率問題は乱数発生させてシミュレーションできるので( ・∀・)イイ!!
臨床医学は確率事象を扱うから。
例. >6の問題
>>219
お前は数学の問題になってない問題をベタベタ張ってくるから邪魔なんだよ能無し
問題文すら作る能力ないなら出てくんなカス >>219
どうせシミュレーションするなら、コロナワクチンの有効性の評価とか、
大幅に増えた超過死亡の原因究明とか、面白そうな題材がそこらへんに
いっぱい転がってないか? b,cは実数とする。
f(x)=x^2+bx+c
g(x)=x^2+bx+csin(x)
とする。
方程式f(x)=0が実数解を持たず、かつ方程式g(x)=0が0でない実数解を持つとき、b,cが満たすべき条件を求めよ。
>>222
>6の計算はコロナネタ。
m3のカンファでコロナ患者接触翌日に発症した症例提示があったら、発症が早すぎるからその接触が感染じゃないのではとの反論がでてオミクロン株ではそれもありうるという議論になっていた。
臨床応用問題
>6のurlのデータと適当な仮定をおいて接触翌日に発症する確率を求めよ。 >>224
なるほど。
そういうことに注力していただけると面白いですね。
高校数学とは縁遠い話なので、このスレが適切とは思えませんが。 >>226
ばっかじゃないの?
分布関数好きになんでも選んでいいならもちろんそんな答えになるはずないやろバーカ
そんな事も分からんパープーのくせにわざわざ数学板にパープーなレスつけて恥ずかしいとすら思えない恥知らず
どこまで能無しやねん? 数研出版の教科書に載ってる場合の数と確率の問題ですが質問が。
A,B,C,Dの4人の名刺が1枚ずつ別々の封筒に入れてある。
この4人がそれぞれ別々の封筒を選ぶとき、次の確率を求めよ、というものの
(2)、「4人とも他人の名刺が入った封筒を選ぶ確率」、という問題で
自分はAが自分以外の名刺を選ぶから3通り、次のBは残りから選ぶから2通り、
その次のC、Dは残りだから1通りだから全部で6通り、それでこの4人の
名刺の選び方は4!だから24分の6で4分の1と出したのですが
教科書ガイドではこの4人とも他人の名刺が入った封筒を選ぶやり方を
わざわざ樹形図を使って9通りだから確率は9÷4!で8分の3が答え、となってました。
自分の考え方のどこが間違ってるのか、テストに出されたとき何を気を付ければ良いのか
良く分らないので教えてください。
>>230
人に質問するのもいいけど自分の答えが6通り、正解が9通りとわかってるんだからどこかに数え漏れがあると考えて自分で探せる能力身につけておかないと勉強が捗らないよ
数え漏れは
>次のBは残りから選ぶから2通り、
この辺から起こってる
実際樹形図見てみたら2個目のBの選択肢が必ずしも2個ではないのがわかるやん? >>231
でも他の問題ではバリバリにCとかPとか使ってるのに
この問題では樹形図から!!っていうのは違和感抱くんですけど。
樹形図でしか出来ない問題とPとかCとか使える問題の差異はどこから
来るんでしょうか? >>230
解答の樹形図を見ても分からないってヤバいな
愚直に具体的に書き並べれば? >>233
だからPとかは枝の分岐数がいつでも一定だから使える
その問題だと1番目の人が2番の人の封筒選んだ場合とそうでない場合で枝の数が変わるからもちろんPなんて使えない
2段目の枝の数違ってんのみたらわかるやん? サイコロを繰り返し振り、1の目が2連続で出たら振ることをやめる。
ちょうどn回目にサイコロを振った時点で、振ることをやめる確率をnで表せ。
>>230
解法(その1)
完全順列の公式を使う
https://ja.wikipedia.org/wiki/%E5%AE%8C%E5%85%A8%E9%A0%86%E5%88%97
a4=9
なので9/4!=3/8
解法(その2)
ひたすら列挙して数える
> pm
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 1 2 4 3
[3,] 1 3 2 4
[4,] 1 3 4 2
[5,] 1 4 2 3
[6,] 1 4 3 2
[7,] 2 1 3 4
[8,] 2 1 4 3
[9,] 2 3 1 4
[10,] 2 3 4 1
[11,] 2 4 1 3
[12,] 2 4 3 1
[13,] 3 1 2 4
[14,] 3 1 4 2
[15,] 3 2 1 4
[16,] 3 2 4 1
[17,] 3 4 1 2
[18,] 3 4 2 1
[19,] 4 1 2 3
[20,] 4 1 3 2
[21,] 4 2 1 3
[22,] 4 2 3 1
[23,] 4 3 1 2
[24,] 4 3 2 1
該当するのは
> pm[apply(pm,1,f),]
[,1] [,2] [,3] [,4]
[1,] 2 1 4 3
[2,] 2 3 4 1
[3,] 2 4 1 3
[4,] 3 1 4 2
[5,] 3 4 1 2
[6,] 3 4 2 1
[7,] 4 1 2 3
[8,] 4 3 1 2
[9,] 4 3 2 1
9/24=3/8 名刺が1~10枚のときの確率を算出(検算希望)
0 1/2 1/3 3/8 11/30 53/144 103/280 323/878 16687/45360 1001/2721
検算希望て 質問者でも出題者でもない新たなカテゴリーが出たな
>>241
俺の使っているRだと不定長整数が扱えないので数が大きくなると誤答を返してくる。 >>239
だから書いとるやろ?
なんで分からんのや能無し >>245
臨床問題
感染した当日に発症する確率を適当な前提を仮定して計算せよ。
の答は? >>245
だから「なんでも仮定入れていいならどんな答えも出せる」
アホですか?
何回この質問させるんや能無し おお、盛り上がってますね。
この調子で除夜の鐘まで頑張ってほすいw
>>230
出題ではなく、まともに質問してるだけたいしたもんだよ。
>自分はAが自分以外の名刺を選ぶから3通り、次のBは残りから選ぶから2通り、
そこがおかしい。Aが3通りはいいが、AがBを選んだ場合、BはA,C,Dの3通り選べる。
よって、A,Bが自分を選ばない組み合わせは、2×2+3=7通りあるのよ。
このうちA,Bが互いを選ぶのは1通りで、その場合、C,Dが自分を選ばないのは1通り。
A,BがC,Dどちらも選ぶのは2通りで、その場合C,DはA,Bどちらかを選べるので2通り、
A,BがCかDどちらかのみを選ぶのは残りの4通りで、その場合、C,Dのうち選ばれ
たほうは選ばれなかった方をとるしかない(さもないと残りはC,Dしかないので
自分を選ぶしかなくなる)ので1通り。
よって全部で1+2x2+4=9通りになるので、確率は9/24=3/8 >>233
場合の数が少なければ、とにかく樹形図を使って数え上げるというのが
検算の意味もあって良いので、試験対策としては覚えておいたほうがいいかもね。
場合の数が多ければ(10人とかね)どうしようもないけどね。
この問題の場合は>>239が示したように完全順列の問題として知られていて、漸化式
a_n=(n-1)(a_(n-2)+a_(n-1))で一般化できる。
このやり方をあてはめれば、Aの名刺の選び方は3通りあるが、
i))Aが選んだ名刺の相手がAの名刺を選んでいる場合、残りの2人は互いの名刺を選ぶ
ことになるので1通りしか選び方はない。
ii))Aが選んだ名刺の相手がA以外の名刺を選んでいる場合は、Aを除いた3人が互いの
名刺を選んでいることになるので、3人が自分の名刺を選ばないとり方は2通り。
よって、全部で3x(1+2)=9通りになる。 >>230
触発されてこういう問題を考えてみた。
100人の名刺を集めてそれをシャッフルして無作為に選んで1人1枚を100人に返す。
自分の名刺が返ってくる人数の期待値とその95%区間を求めよ
シミュレーションすると期待値1人、95%信頼区間は0-3
厳密解は知らん >>250
>Aが選んだ名刺の相手がA以外の名刺を選んでいる場合は、Aを除いた3人が互いの
名刺を選んでいることになるので、
説明不足かもしれないので、補足しておくと、Aが選択したあとにはAの名刺を含む3枚の
名刺が残っているが、Aが選んだ名刺の相手はAの名刺を選べないということは、場に残った
Aの名刺を、Aが選んだ名刺で置き換えて3人に選ばせても同じことになる。
たとえば、AがBの名刺をとった場合、場にはBの名刺はなくAの名刺が残っている。
それをBの名刺で置き換えれば、Bはそれを選べないが、C,Dは選ぶことができるので、
場合の数は同じになる。 b,cは実数とする。
f(x)=x^2+bx+c
g(x)=x^2+bx+csin(x)
とする。
方程式f(x)=0が実数解を持たず、かつ方程式g(x)=0が0でない実数解を持つとき、b,cが満たすべき条件を求めよ。
>>247
臨床問題
感染した当日に発症する確率を適当な前提を仮定して計算せよ。
の答は? >>251
自分の名刺が返ってくる確率は1/100なので期待値は100*1/100=1
要素数nの完全順列の総数をa_nとすれば、
自分の名刺が返ってくる人数が0人である確率P(0)は a_100/100!
1人である確率はP(1)= C(100,1)a_99/100!=a_99/99!
2人である確率はP(2)=C(100,2) a_98/100! =(1/2!)a_98/98!
3人である確率は P(3)=C(100,2)a_97/100! =(1/3!) a_97/98!
...
a_100/100! ≒a_99/99!≒a_98/98!≒a_97/97!≒ 1/e
であることから、
P(0)+P(1)+P(2)≒ (1+1+1/2!)/e ≒2.5/2.718≒0.920
P(0)+P(1)+P(2)+P(3) ≒ (1+1+1/2!+1/3!)/ e ≒2.6667/2.718≒0.981 >>254
お前のパソコンにはなんか数字が出ててそれを“答え”になる問題を作った気分なんやろ
能無しが底抜け 皆さんありがとうございます、
完全順列で、同様に確からしくないということですね。
気を付けます
>>253
傑作質問なのでご回答お願い申し上げます >>257
んで、感染した当日に発症する確率は、いくつよ? >>237
シミュレーションしてnの分布をだすと

んで、確率は

>>255
解答のレスありがとうございました。
自分の名刺が返ってくる人数はどんな分布になるのかシミュレーションしてみたら

100人の名刺を集めてそれをシャッフルして無作為に選んで1人1枚を100人に返す。
自分の名刺が返ってくる人数を当てる賭けをする。
何人に賭けるのが最も有利か?
お前のクズ文章が数学の体をなしてないのはこの板の住人には全員わかってる
お前ただ1人そのことに気づけず永遠に恥を晒し続けてる能無しの恥知らず
それがお前の人生の終着点だよ
前>>176
>>263
自分の名刺が自分に返ってくる確率は1/100
100人いるから(1/100)×100=1
∴一人に賭ける。 >>253
h(x)=sin(x)/x とする h'(x)=(cos(x)x-sin(x))/x^2=(cos(x)-h(x))/x
tを正とし h(x)のx=tでの接線は y=h(t)+(x-t)(cos(t)-h(t))/t
これが(0,1)を通るとき 1=h(t)+(0-t)(cos(t)-h(t))/t=2h(t)-cos(t)
(1+cos(t))/2=h(t)=sin(2t/2)/t=2sin(t/2)cos(t/2)/t=h(t/2)cos(t/2)
(cos(t/2)^2=h(t/2)cos(t/2) t/2=uとし cos(u)(cos(u)-h(u))=0
ucos(u)-sin(u)=u(cos(v)-vsin(v)-cos(v))=-uvsin(v) なるvが0<v<uにある
右辺はu<πのとき負だから cos(u)(cos(u)-h(u))=0の最小の解はu=π/2
t=πのときの接線は y=h(t)+(x-t)(cos(t)-h(t))/t=0+(x-π)(-1-0)/π=1-x/π
このとき(0,1)と(π,0)の二点を通るので (0,1)と(m,0)を通る直線は
0<m<πのとき y=h(x)と共有点を持てず π≦mのとき明らかに共有点を持つ
(0,1)を通る直線がy=h(x)と共有点を持つ条件は 0<傾きの絶対値<1/π
c=0のときf(x)=g(x)になるので解なし c≠0で考える
y=-x/c-b/cが (0,1)を通りy=h(x)と共有点を持つには b=-cかつπ<│c│
これとb^2-4c<0を合わせると、cは正で、c(c-4)<0だから π<c<4、b=-c
このときy=-x^2-bxとy=csin(x)はx=0以外の共有点を持つので題意を満たす >>53
∫[-∞,s]f(x)dx=2/3なるsがあるがこのとき∫[s,∞]f(x)dx=1/3だからg(s)がない >>265
レスありがとう。
問題にケチをつけるしか能のない罵倒厨と違って
東大卒の人物は答をだそうと試みるんだなぁと感服。
答は違うと思うけど。
要素数nの完全順列の総数をanと表記する
0人の確率p0=a100/100! と 1人の確率p1=a99/99!の大小比較になる。
p0-p1 = a100/100!-a99/99! = (1/100!)(a100-100*a99)
なので
a100-100*a99と0の大小を比較すればいい
a(n)=n*a(n-1) + (-1)^n
という漸化式が成り立つという
https://ja.wikipedia.org/wiki/%E5%AE%8C%E5%85%A8%E9%A0%86%E5%88%97
a100-100a99=(-1)^100=1>0なので
p0>p1が結論できる。
完全順列をプログラムに計算させて比較
> a100
[1] 34332795984163804765195977526776142032365783805375784983543400282685180793327632432791396429850988990237345920155783984828001486412574060553756854137069878601
> 100*a99
[1] 34332795984163804765195977526776142032365783805375784983543400282685180793327632432791396429850988990237345920155783984828001486412574060553756854137069878600
確かにその差は1なので正しい計算をしているだろうと思う。
結論 : 0人にかけた方が有利。
その確率の差は1.07151*10^(-158)
シミュレーションで検出できる差じゃないな。 >>237
発展問題
サイコロを繰り返し振り、1の目が3連続で出たら振ることをやめる。
サイコロを振る回数の期待値を求めよ
朝飯前にプログラムして回数の分布をシミュレーションした結果

厳密解は知らん。 >>43
kが奇数で0<t<πのとき sin(kπ-t)=sint>0 |sin(kπ-t)|=sin(kπ-t)=sint
kが偶数のとき sin(kπ-t)=-sint<0 |sin(kπ-t)|=-sin(kπ-t)=sint
a[k]=1/(1+(kπ/n)^2)と置く kπ/n=tanθ dk/dθ=n/π/(cosθ)^2
Σ[k=1,2n]a[k]>∫[1,2n]a[k]dk=n/π∫[arctan(π/n),arctan(2π)]dθ
Σ[k=1,2n]a[k-1]<1+Σ[k=1,2n]a[k]<1+∫[0,2n]a[k]dk=1+n/π*arctan(2π)
2Σ[k=1,2n]a[k-1]/n→arctan(2π)/π 2Σ[k=1,2n]a[k]/n→arctan(2π)/π
b[n]=∫[0,2π] |sin(nx)|/(1+x^2) dx=1/n∫[0,2nπ] |sin(t)|/(1+(t/n)^2) dx
=1/nΣ[k=1,2k]∫[(k-1)π,kπ] |sin(t)|/(1+(t/n)^2) dx
=1/nΣ[k=1,2k]∫[0,π] |sin(kπ-t)|/(1+((kπ-t)/n)^2) dx
=1/nΣ[k=1,2k]∫[0,π] sint/(1+((kπ-t)/n)^2) dx
1/nΣ[k=1,2k]a[k]∫[0,π]sintdx<b[n]<1/nΣ[k=1,2k]a[k-1]∫[0,π]sintdx
2Σ[k=1,2k]a[k]/n<b[n]<2Σ[k=1,2k]a[k-1]/n 与式=arctan(2π)/π >>237
n回目で止まる確率をp(n)とする
p(1)=0 p(2)=1/6^2
n>2のとき 一回目が1の目で二回目が1以外でn回目で止まる
または1回目が1以外が出てn回目で止まるかだから
p(n)=1/6*5/6*p(n-2)+5/6*p(n-1)
和が5/6で積が5/36である数をa,bとする
p(n)-ap(n-1)=b(p(n-1)-ap(n-2))=b^(n-2)(p(2)-ap(1))=b^(n-2)/36
p(n)-bp(n-1)=a^(n-2)/36 とa,bを入れ替えると
(b-a)p(n-1)=(b^(n-2)-a^(n-2))/36だから
p(n)=(b^(n-2)-a^(n-2))/(b-a)/36 >>273間違えた
b[n]→2arctan(2π)/πだ >>274
>和が5/6で積が5/36である数をa,bとする
a=5/12+sqrt(5)/12
b=5/12-sqrt(5)/12
として
P(n)=(b^(n-2)-a^(n-2))/(b-a)/36
P(1)=-0.2
P(2)=0
になりましたが 100^99 と 99^100
どっちが大きいか?
>>270
間違えた 修正
c≠0としてよい 直線y=-x/c-b/cの傾きは0でない
y切片が1より大きい直線のとき 傾きが正であればy=h(x)とx<0で共有点を持ち
傾きが負ならx>0に共有点がある
y切片が1未満の直線は傾きが負ならx<0に確実に共有点がある
傾きが正ならx>0に確実に共有点がある
y=-x/c-b/cがy=h(x)と共有点を持つ
↔y切片が1でないかまたはy切片が1で傾きの絶対値が1/π以下である
↔b≠-c または b=-cかつπ≦│c│
これとb^2-4c<0を合わせると
b^2<4cかつb≠-c または b^2<4cかつb=-cかつπ≦c<4 だから
b^2<4c かつ (b≠-c または π≦c<4) pn(n) = (2*sqrt(5)*(5/12+sqrt(5)/4)^n+(15+7*sqrt(5))*(1/12*(5-3*sqrt(5)))^n)/(75+45*sqrt(5))
漸化式 一般解 シミュ
[1,] 0.00000000 0.00000000 0.00000
[2,] 0.02777778 0.02777778 0.02867
[3,] 0.02314815 0.02314815 0.02328
[4,] 0.02314815 0.02314815 0.02376
[5,] 0.02250514 0.02250514 0.02200
[6,] 0.02196931 0.02196931 0.02151
[7,] 0.02143347 0.02143347 0.02155
[8,] 0.02091252 0.02091252 0.02121
[9,] 0.02040397 0.02040397 0.01978
[10,] 0.01990782 0.01990782 0.01932
[11,] 0.01942374 0.01942374 0.02050
[12,] 0.01895142 0.01895142 0.01856
[13,] 0.01849059 0.01849059 0.01932
[14,] 0.01804097 0.01804097 0.01803
[15,] 0.01760228 0.01760228 0.01780
[16,] 0.01717426 0.01717426 0.01721
[17,] 0.01675664 0.01675664 0.01691
[18,] 0.01634918 0.01634918 0.01639
[19,] 0.01595163 0.01595163 0.01603
[20,] 0.01556374 0.01556374 0.01553

>>277
n>2って前提になってるから、そこは問題ないでしょ。
どっちみち間違ってるけどねw >>278
99log[10]100-100log[10]99=99*2-100(2+log[10](1-1/100))
=-2-100log(1-1/100)/log10
<-2-100(-Σ[k=1,∞](1/100)^k)=-2+100/99<0 100^99=(99+1)^99=99^99 + C(99,1)99^98+…+C(99,k)99^(99-k)+…+99^2+1
右辺の各項は最大でも99^99かそれより小さいので
(なんとならば k≧2で、 C(99,k)=99・98…(99-k+1)/k! < 99^k )
100^99 < 98・99^99 +99^2+1 < 98・99^99 + 99^99 =99^100
>>284の補足
一般化すると、
n≧3で (n+1)^n <(n-1)n^n +n^2+1
かつ、n^2+1< n^nが成り立つことから、
(n+1)^n < n^(n+1) となる >>274また間違ってたからやり直し
和が5/6で積が-5/36である数をa,bとする
p(n)-ap(n-1)=b(p(n-1)-ap(n-2))=b^(n-2)(p(2)-ap(1))=b^(n-2)/36
p(n)-bp(n-1)=a^(n-2)/36 とa,bを入れ替えると
(b-a)p(n-1)=(b^(n-2)-a^(n-2))/36だから
p(n)=(b^(n-1)-a^(n-1))/(b-a)/36
nをn+1に置き換えたからn>1で成り立つがn=1でも成り立つ >>271
名刺の枚数が奇数のときは1人に賭けた方が有利になるってことだな。 >>278
99^100の末尾の数字はいくつか?
答 1
99^100=9^100*11^100=81^50*11^100
検算
36603234127322950493061602657251738618971207663892369140595737269931704475072474818719654351002695040066156910065284327471823569680179941585710535449170757427389035006098270837114978219916760849490001 >>289
簡単だよ。
末尾が9となる数字のべきの末尾は9のべきの末尾になるが、
9のべきの末尾は9と1が交互に出てくるだけだから、
奇数乗では9、偶数乗では1になる。 525
797
1069
1341
1613
も該当
検算希望
4桁まで探しだす。
> n[f(n)]
[1] 253 525 797 1069 1341 1613 1885 2157 2429 2701 2973 3245 3517 3789
[15] 4061 4333 4605 4877 5149 5421 5693 5965 6237 6509 6781 7053 7325 7597
[29] 7869 8141 8413 8685 8957 9229 9501 9773
5^nがmod289で3
一番大きい9773Wolfram先生に検算してもらった。
https://www.wolframalpha.com/input?i=5%5E9773+mod289&lang=ja 5桁まで
253 525 797 1069 1341 1613 1885 2157 2429 2701 2973
3245 3517 3789 4061 4333 4605 4877 5149 5421 5693 5965
6237 6509 6781 7053 7325 7597 7869 8141 8413 8685 8957
9229 9501 9773 10045 10317 10589 10861 11133 11405 11677 11949
12221 12493 12765 13037 13309 13581 13853 14125 14397 14669 14941
15213 15485 15757 16029 16301 16573 16845 17117 17389 17661 17933
18205 18477 18749 19021 19293 19565 19837 20109 20381 20653 20925
21197 21469 21741 22013 22285 22557 22829 23101 23373 23645 23917
24189 24461 24733 25005 25277 25549 25821 26093 26365 26637 26909
27181 27453 27725 27997 28269 28541 28813 29085 29357 29629 29901
30173 30445 30717 30989 31261 31533 31805 32077 32349 32621 32893
33165 33437 33709 33981 34253 34525 34797 35069 35341 35613 35885
36157 36429 36701 36973 37245 37517 37789 38061 38333 38605 38877
39149 39421 39693 39965 40237 40509 40781 41053 41325 41597 41869
42141 42413 42685 42957 43229 43501 43773 44045 44317 44589 44861
45133 45405 45677 45949 46221 46493 46765 47037 47309 47581 47853
48125 48397 48669 48941 49213 49485 49757 50029 50301 50573 50845
51117 51389 51661 51933 52205 52477 52749 53021 53293 53565 53837
54109 54381 54653 54925 55197 55469 55741 56013 56285 56557 56829
57101 57373 57645 57917 58189 58461 58733 59005 59277 59549 59821
60093 60365 60637 60909 61181 61453 61725 61997 62269 62541 62813
63085 63357 63629 63901 64173 64445 64717 64989 65261 65533 65805
66077 66349 66621 66893 67165 67437 67709 67981 68253 68525 68797
69069 69341 69613 69885 70157 70429 70701 70973 71245 71517 71789
72061 72333 72605 72877 73149 73421 73693 73965 74237 74509 74781
75053 75325 75597 75869 76141 76413 76685 76957 77229 77501 77773
78045 78317 78589 78861 79133 79405 79677 79949 80221 80493 80765
81037 81309 81581 81853 82125 82397 82669 82941 83213 83485 83757
84029 84301 84573 84845 85117 85389 85661 85933 86205 86477 86749
87021 87293 87565 87837 88109 88381 88653 88925 89197 89469 89741
90013 90285 90557 90829 91101 91373 91645 91917 92189 92461 92733
93005 93277 93549 93821 94093 94365 94637 94909 95181 95453 95725
95997 96269 96541 96813 97085 97357 97629 97901 98173 98445 98717
98989 99261 99533 99805
>>299
プログラム(R言語)に割り算させただけ。
Haskellと違って不定長整数に対応していないので
大きな数になると誤答が返ってくることもままあるので
みつかった答はWolframで検算。 60年たっても有限環の可逆元のなす群の位数の話すら分からん能無しがまたひとつ恥を晒す
恥の書き収めの最後にしたらどうや?
m, b, c から c = b^e mod m なる e を求める問題は離散対数問題といわれ、効率的な、つまり入力サイズの多項式時間のアルゴリズムは発見されていない。公開鍵暗号のうちある種のものは、この一方向性を利用して設計されている。
だってさ。
>>300
R(n) を 5^n の 298を法とする剰余とする。
5R(n)が298を越えてなければ、R(n+1)=5R(n)
5R(n)が298を越えていたら、R(n+1)=5R(n) - 298[5R(n)/298]
というアルゴリズムで、n=1から初めて、順次5^nの剰余を計算していけば
誤差は出ないと思うよ。 nCr=n!/r!(n-r)!から、nCr=nCn-r
になる事とその意味は理解できたのですが、
逆にこのnCr=n!/r!(n-r)!という式だけ与えられた場合に、どういう手順を踏んでいけば=nCn-rへと変形させられるかわかりません。
ご教授いただけると嬉しいです。
mod 289で
5^272≡1
5^253≡3
なので
n=272m+253 (mは非負整数)にすればいくらでも解がだせるな。
1億以下でこれをみたす数は
> 100000000/272
[1] 367647.1
なので
367647個で総当りで数えた>308の個数と一致。
今年は10年ぶりぐらいに高校数学の復習しようと思ってるんだけどおすすめの参考書や問題集とかありますか?
当時は理系で数Ⅲまでやったけどかなり忘れてる
大学への数学1年間購読とかでいいのかな
>>292
演習問題
5^nがmod2023で3になるnを求めよ。
> calc(5,3,2023)
816k + 797 816k + 1613 >>313
ありがとう、存在は知ってたけど忘れてた
良い機会なので読んでみます あけましておめでとうございます。
今年も質問いたしますのでよろしくお願いいたします。
p,qを素数とする。2次方程式
x^2-px+q=0
が相異なる整数解を持つような(p,q)をすべて決定せよ。
解をa,b (a<b)とすると
q=a*bが素数だからa=1
p=a+b=1+b
pは素数なので奇数
するとbは偶数
q=a*b=1*b=bが素数なので偶数の素数は2のみ。
ゆえにb=2
q=a*b=2
p=a+b=3
>>308,309
剰余群が有限巡回群になるのは分かってるんだから、R(N)=1になる N(>1)
があれば、位数Nでしょ。
だから計算しなくてもR(n)=3になるnは周期Nの繰り返しになるに >>306
nCrの定義式のrにn-rを代入するだけでしょ。
nC(n-r )= n!/(n-r)!(n-(n-r))! =n!/(n-r)!r! =nCr >>315
新年早々おめでたい奴だな。
それは質問じゃなくて出題だと何回言えば分かるの?
顔を洗って出直してこい! >>319
>>307
回答くださりありがとうございます!
n-(n-r)=rを代入するのに、まずrってnからrじゃないものを引いたものだ!って気づいてから行うなら納得できるのですが、逆にまず式の変形だけでr=n-(n-r)という形を完成させ、その結果同様の結論に至りたいのですがやり方がわからず… >>310
何が目的ですか?
家庭教師とかなら基礎問題精講あたりさらっと通読すればいい。 >>315
今年も出題を楽しみにしております。
p,qをプログラムに探索させようと始めたら答を思いついてしまって拍子抜けしましたが、まぁ楽しめました。 >>321
何事にも理由があるとは思わないことです
式だけで考えればそうなってるから以外に答えようがありません
式の意味で考えれば、n個からr個のものを選ぶということは、n-r個の選ばれなかった物を選ぶことと同じだということです >>323
おめでたい出題をよろしく!
答が提示されたら用意した答とあっているか否かのコメントがある嬉しいのでそれもよろしくお願いします。 >>326
おめでたいのはお前の頭だよ。
答えを用意してるのなら、それを提示して「これであってますか?」と質問するのが筋だろ。
ろくでなしもいいとこ。正月早々死んでくれ。 >>304
「5^253を289で割った余りを求めよ」のような問題はよく見るのに
「5^nを289で割った余りが3になるnを求めよ」という問題を見かけないのは
こちらのタイプの問題が研究されると暗号が破られて危険なので
このような問題は出題するのも解くのもよろしくない
ということなんですね。 >>329
>305のアルゴリズムに従ってプログラムしたらオーバーフローもなくて簡単に計算できたから暗号破りは大袈裟では?
ちなみに
>305 助言を喜びとする人
>303 罵倒を喜びとする人(チンパンジーが好きらしい)
高校生の諸君はどちらのような人間になりたいですか? 暗号用に使われる鍵の長さは1024ビット以上だそうです
300桁くらいになるみたいですね
暗号を解読するには、(300桁)^(n)を(300桁)で割った余りが(300桁)になるnを求めないといけません
桁がこれだけ増えても通用するようなアルゴリズムがもしもあるなら、暗号解読されちゃいそうですけどまあ無理でしょうね
なんにしても、nを求めるのは総当たりしか基本なくてつまらない問題にならざるを得ないので、高校の問題ではあまりでないのです
一家の大黒柱なのに正月早々他人に出題をおねだりする人でなければどちらでもいいです
>>331
5^nがmod 1323110702248772088961881918116579338750386936838809670378412731441 で3になるnはありますか? >>332
富岳は4X10^17Flopsの演算速度らしいですが、 仮に毎秒10^18ステップの
剰余計算ができたとしても、10^300ステップをこなすには宇宙の年齢(~10^18秒)
をはるかに越えてしまいます。 >>328
いや、>315の問題が答と一緒に投稿されたらつまらんね。 >>336
質問につまらんもつまるもあるか、馬鹿。
おまえ頭悪すぎだわ。 質問です。
∫[0,π/2] {sin(x)}^n dx < 1/8
となる最小の自然数nを求めよ。
という問題が分からないので教えてください。
>>340
チンパンジーフェチによれば
答えを用意してるのなら、それを提示して「これであってますか?」と質問するの筋
だって >>339
問題が分からないのなら答えを見ても分かるわけないなw
誰か問題を解説してやれよwww >>343
質問です。
∫[0,π/2] {sin(x)}^n dx < 1/8
となる最小の自然数nを求めよ。
という問題の正答に至るまでの道筋が分からないので教えてください。 aを実数とする。
x^4+a^2を実数係数の多項式の積に因数分解せよ。
>>345
この先をまっすぐ行って、3つめの信号を左に曲がってから全力疾走すればたどり着く ∫[0,π/2]=(sinx)^ndx=I[n]
I[0]=π/2 I[1]=1 n>2のとき I[n]=-∫[0,π/2](cosx)'(sinx)^(n-1)dx
=0+∫[0,π/2](cosx)^2(n-1)(sinx)^(n-2)dx=(n-1)(I[n-2]-I[n])
I[n]=(n-1)/n*I[n-2]
I[2n]=π/2*(2n-1)!!/(2n)!! I[2n+1]=(2n)!!/(2n+1)!!
(2n-1)!!/(2n)!!=(2n)!/(2n)!!^2=(2n)!/(n!2^n)^2
=(√(2π)(2n)^(2n+1/2)e^(-2n+1/(24n)-t/(360*(2n)^3))
/(2π*n^(2n+1)e^(-2n+1/(6n)-u/(180n^3)*2^(2n))
=(2π)^(1/2-1)n^(1/2-1)2^(2n+1/2-2n)*e^(-1/(8n)+(16u-t)/(180*16n^3))
=1/√(nπ)*e^(-1/(8n)+(16u-t)/(180*16n^3)) t,uは0と1の間の数
I[2n]≒√(π/n)/2=1/8とするとn≒16π≒50
n=50のとき (2n-1)!!/(2n)!!=1/√(50π)*e^(-1/400+(16u-t)/(180*16n^3))
>1/√(50π)*e^(-1/400+(16*0-1)/(180*16*50^3))
>1/√(50π)*e^(-1/400+(16*0-1)/10^8)>1/√(50π)*(1-1/400-10^-8)
I[100]>√(π/200)*(1-1/400-10^-8)>0.12501>1/8
I[101]=π/2/I[100]/101<π/202/0.12501<0.1245<1/8 n=101
>>339
101
> f=\(n) integrate(\(x) sin(x)^n, 0,pi/2)$value - 1/8
> ceiling(uniroot(f,c(1,1e3))$root)
[1] 101 >>334
プログラム組んだから
m=as.bigz(1323110702248772088961881918116579338750386936838809670378412731441)
n=1
while(5^n%%m!=3) n=n+1
答がでるまで10^18秒くらい待ってくれ。 質問です、
lim[n->∞] ∫[0,π/2] {sin(x)}^(1/n) dx の 値がπ/2になるようなのですが、その道筋が分からないので教えてください。
因数分解って何のためにするの?
式を簡単にするため?
例えば
15+24
=(3×5)+(2×3×4)
=3(5+(2×4))
=3(5+8)
でもこれだと何が良くなったのかよく分かんない
例がダメなのかな?
イマイチピンとこない
Nは正の整数とする。
N!が10^40で割り切れる時の最小のnを求めよ。
この問題の解答で、5の指数で大雑把に絞り込みする。
5→25
5^2→5
5^3→1 の合計31と絞り込む、
5^3より大きな5の倍数を小さい順に書き出すと
130,135,140,145,150,155,160,165,170….
であり、それぞれが持つ素因数5の個数は
1,1,1,1,2,1,1,1,1…
よって、40=31+1+1+1+1+2+1+1+1であるから、
165!が5^40の倍数であると言える。
と書かれてたんだけど、
素因数5の個数が130=1、135=1…
ってなんで書けるのか教えてほしい。
>>358
たとえば、x^2 +3x-4=0という方程式を解きたいとすると、
左辺を因数分解して(x-1)((x+4)=0と置き換えれば、
x-1=0またはx+4=0を満たせばよいということで、x=1,-4
という解が簡単に求まるでしょ。 >>359
130=5・26→素因数分解すると5は1個だけ
135=5・27→ 〃
・
・
150=5・30=5^2・6→5は2個
155=5・31→5は1個
・
・
ってことでしょ。
自然数は5つおきに5の倍数
5の倍数は5つおきに25=5^2の倍数
25の倍数は5つおきに5^3=125の倍数
etc. x,yが整数で
33x - 136y
3x - 272y
がともに21の倍数になるとき
xは7の倍数でyは21の倍数
といえますか。
>>356
任意の0<t<π/2に対して
∫[0,π/2]{sinx}^(1/n)dx>∫[0,t]{sint/2}^(1/n)dx+∫[t,π/2]{sint}^(1/n)dx
={sint}^(1/n){t/2^(1/n)+π/2-t}>{sint}^(1/n){π/2-t/2}
右辺がπ/2-tより大きいとき{sint}^(1/n)>(π/2-t)/(π/2-t/2)=(1-2t/π)/(1-t/π)
n>log{sint}/{log(1-2t/π)-log(1-t/π)} これを満たす最小の整数nをNとする
任意のtに対して常にNがあってNより大きい任意のnに対して
│∫[0,π/2]{sinx}^(1/n)dx-π/2│<t >>279まだ間違ってたので再修正
c≠0 かつ b^2<4c かつ (b≠-c または π≦c<4) >>278
x≧e、y>0のとき xlog(x+y)=x(logx+log(1+y/x))<x(logx+y/x)≦(x+y)logx 質問です
Nは正の整数とする。
N!が10^100で割り切れる時の最小のNを求めよ。
の答は405でよろしいでしょうか?
>>363
ありがとうございました。
π/2で納得がいきました。 自分の答が正しいかどうかわからないので質問します。
ニュー速+の 1月の住宅ローン固定金利、約9年半ぶり高水準 大手5行
のスレに
金利が0.25%あがると総支払額が200万円増える
という投稿があった。
借入期間を35年とし、月利は年利の1/12で計算する。
返済は毎月の返済額が一定の元利均等返済方式とする。
(1)この投稿者が年利3%でローンを組んでいたときに借入金はいくらか計算せよ。
(2)この投稿者が4000万円のローンを組んでいたときに利上げ前の年利はいくらか計算せよ。
サイコロの1の目のでる確率が常に1/6というのは空想の世界である。
リアルワールドの問題を考える。
やや歪なサイコロを100回振って1の目の出る回数を記録するという作業を10回行ったところ
1の目のでた回数は各100回中
12 17 13 18 20 9 14 19 15 14
であった。
(1)このサイコロの1の目のでる確率の95信頼区間を求めよ。(答は小数3桁まででよい)
(2)このサイコロを振って1の目が2回続けてでるまでの回数をnとする。
nの期待値とその95%信頼区間を求めよ(答は整数でよい)。
シミュレーションや信頼区間の算出流儀は一義的ではないので質問しました.
>>359
一般化すると
Nまでの自然数に素因数として含まれる5の個数が総計n個ある必要がある。
5の倍数は5を素因数として含むが、 そのうち5^2の倍数は2個、5^3は3個...含むので、
Nより小さい5の累乗の指数のうち最大のものをmとして、5の因数の総計f(N)は、
f(N)=[N/5] + [N/5^2] + [N/5^3]+…+[N/5^m]
よって、f(N)≧n であればN!は5^nで割り切れる。
N!に対する2の素因数の総計g(N)も同様にして求められるが、g(N) > f(N)は明らかなので、
f(N)≧nであれば、N!は10^n=2^n・5^nで割り切れる。
このようなNのうち最小のものは、n=[N/5] + [N/5^2] + [N/5^3]+…+[N/5^m]
の解として求まる。けど、簡単には求まらないので試行錯誤が必要?
n=40の場合、[5/N]=40となる最小のNは200で対応するmは3なので、
f(200)=[200/5] + [200/5^2] + [200/5^3]=40+8+1=49
200は5^2の倍数なので5^3の倍数である125までは、25ずつ減らすと
f(N)は6減るので、f(175)=43
あと5ずつ減らしていくと、f(170)=41, f(165)=40。ばんざーい! >>370
[ x ] はxを越えない整数を表す記号 >>366
検算は簡単。
>>370に従って、
f(405)=[405/5] +[405/25] +[405/125] =81+16 + 3 =100
なので正解。 厳密に言えば、f(404)=99なので、405がf(N)=100を満たす最小の解と断る
必要あり?





 は
は