【質問者必読!!】
まず>>1-4をよく読んでね
数学@2ch掲示板用 掲示板での数学記号の書き方例と一般的な記号の使用例
http://mathmathmath.dotera.net/
・まずは教科書、参考書、web検索などで調べるようにしましょう。(特に基本的な公式など)
・問題の写し間違いには気をつけましょう。
・長い分母分子を含む分数はきちんと括弧でくくりましょう。
(× x+1/x+2 ; ○((x+1)/(x+2)) )
・丸文字、顔文字、その他は環境やブラウザによりうまく表示できない場合があります。
どうしても画像を貼る場合はPCから直接見られるところに見やすい画像を貼ってください。
ピクトはPCから見られないことがあるので避けてください。
・質問者は名前を騙られたくない場合、トリップを付けましょう。
(トリップの付け方は 名前(N)に 俺!#oretrip ←適当なトリ)
・質問者は回答者がわかるように問題を書くようにしましょう。
でないと放置されることがあります。
(変に省略するより全文書いた方がいい、また説明なく習慣的でない記号を使わないように)
・質問者は何が分からないのか、どこまで考えたのかを明記しましょう。
それがない場合、放置されることがあります。
(特に、自分でやってみたのに合わないので教えてほしい、みたいなときは必ず書くように)
・回答者も節度ある回答を心がけてください。
・970くらいになったら次スレを立ててください。
※前スレ
高校数学の質問スレPart405
http://2chb.net/r/math/1592497360/ [2] 主な公式と記載例
(a±b)^2 = a^2 ±2ab +b^2
(a±b)^3 = a^3 ±3a^2b +3ab^2 ±b^3
a^3±b^3 = (a±b)(a^2干ab+b^2)
√a*√b = √(ab), √a/√b = √(a/b), √(a^2b) = a√b [a>0, b>0]
√((a+b)±2√(ab)) = √a±√b [a>b>0]
ax^2+bx+c = a(x-α)(x-β) = 0 [a≠0, α+β=-b/a, αβ=c/a]
(α,β) = (-b±√(b^2-4ac))/2a [2次方程式の解の公式]
a/sin(A) = b/sin(B) = c/sin(C) = 2R [正弦定理]
a = b cos(C) + c cos(B) [第一余弦定理]
a^2 = b^2 + c^2 -2bc cos(A) [第二余弦定理]
sin(a±b) = sin(a)cos(b) ± cos(a)sin(b) [加法公式]
cos(a±b) = cos(a)cos(b) 干 sin(a)sin(b)
log_{a}(xy) = log_{a}(x) + log_{a}(y)
log_{a}(x/y) = log_{a}(x) - log_{a}(y)
log_{a}(x^n) = n(log_{a}(x))
log_{a}(x) = (log_{b}(x))/(log_{b}(a)) [底の変換公式]
f'(x)=lim_[h→0] (f(x+h)-f(x))/h [微分の定義]
(f±g) ' = f '±g '、(fg) ' = f'g+fg',
(f/g) ' = (f 'g-fg ')/(g^2) [和差積商の微分]
[3] 基本的な記号の使い方は以下を参照してください。
その他については>>1のサイトで。
■ 足し算/引き算/掛け算/割り算(加減乗除)
a+b → a 足す b (足し算) a-b → a 引く b (引き算)
a*b → a 掛ける b (掛け算) a/b → a 割る b (割り算)
■ 累乗 ^
a^b a の b乗
a^(b+1) a の b+1乗
a^b + 1 (a の b乗) 足す 1
■ 括弧の使用
a/(b + c) と a/b + c
a/(b*c) と a/b*c
はそれぞれ、違う意味です。
括弧を多用して、キチンと区別をつけてください。
■ 数列
a[n] or a_(n) → 数列aの第n項目
a[n+1] = a[n] + 3 → 等差数列の一例
Σ[k=1,n] a_(k) → 数列の和
■ 積分
"∫"は「せきぶん」「いんてぐらる」「きごう」「すうがく」などで変換せよ。
(環境によって異なる。) ∮は高校では使わない。
∫[0,1] x^2 dx = (x^3)/3|_[x=0,1]
■ 三角関数
(sin(x))^2 + (cos(x))^2 = 1, cos(2x) = (cos(x))^2 - (sin(x))^2
■ ヴェクトル
AB↑ a↑
ヴェクトル:V = [V[1],V[2],...], |V>, V↑, vector(V)
(混同しない場合はスカラーと同じ記号でいい。通常は縦ヴェクトルとして扱う。)
■行列
(全成分表示):M = [[M[1,1],M[2,1],...],[M[1,2],M[2,2],...],...], I = [[1,0,0,...],[0,1,0,...],...]
(行 (または列) ごとに表示する. 例)M = [[1,-1],[3,2]])
■順列・組合せ
P[n,k] = nPk, C[n.k] = nCk, H[n,k] = nHk,
■共役複素数
z = x+iy (x,yは実数) に対し z~ = x-iy 立てますた。
前スレ逝去 19:25:17.75
当スレ誕生 20:09:37.47
「チンチロリン」の「目」の出る確率って、モンティ・ホール問題みたいでよく分かりません。
nを6以上の自然数とするとき
a+b+c=n , 0<a<b<c を満たす自然数a,b,cの組(a,b,c)の個数をnの式で表すことはできますか。
ただ、nの式の意味が不明瞭なので、あなたの想定によっては不可能です
1/((1-x)(1-x^2)(1-x^3))をべき展開したときの(n-6)次の係数かな
>>7
はい、できます。
(n-1)(n-5)/12 + d_2 /4 + _3 /3,
d_2 = {1 + (-1)^n}/2 = (nが偶数のとき1, nが奇数のとき0)
d_3 = {1 + ω^n + (ω~)^n}/3 = (nが3の倍数のとき1, 他は0)
なお b = b' +1, c = c" +2 とおくと、
求めるものは
a+b'+c" = n-3, 0<a≦b'≦c" を満たす自然数の組(a,b',c")の個数
これを制限つき分割数 q_3(n-3) と云うらしい。 (n-1)(n-5)/12 + d_2 /4 + d_3 /3,
でした。スマソ
マンホールの穴が1辺の長さ1の正方形で
マンホールの空間は正方形が底面の四角柱の形とする。
1辺の長さ1よりごくわずかに大きい正方形の蓋でマンホールが覆われているとする。
マンホールの正方形の対角線方向に蓋の1辺を一致させると蓋を落下させることができる。
1辺の長さが1の正7角形のマンホールであったときに正7角形の蓋を落下させることができるか?
プログラミング知恵遅れを禁止しろよ
頼まれもしないのに1人でシミュレーションしてオナニー見せ付けられるのはうんざりだわ
>>11-12
nを3以上の自然数とするとき
a+b=n , 0<a<b を満たす自然数の組(a,b)の個数は
q_2(n-1) = [ (n-1)/2 ] = (n-1 - d_2)/2.
を使う。 >>13
厚み次第だが、十分に薄ければ別に7角形だけではなく一般の正(2n+1)角形でできる。
正多角形の1辺を底辺とし、その辺から1番遠い頂点から引いた2本の対角線を等辺とする二等辺三角形について
蓋の方の二等辺三角形の対称の軸を穴の方の対角線の方向に合わせればよい。 >>16
正2n角形でも、高さを対角線に合わせれば落下するのでは? >>16
n=1で正三角形だと落下しない気がする。 >>18
いや、三角形でも落下するな。正多角形は全部落下するでいいのでは。 >>16
わかりやすいように、作図してみました。

赤の高さの線が青の対角線に一致するようにすれば落下しますね。
マンホールの7角形の1辺の長さを1とすると
> manhole(7,axes=F)
$対角線
[1] 2.246979604
$高さ
[1] 2.190643134
$落下
[1] TRUE >>20
こういう問題ができる。
1辺の長さが1の正7角形のマンホールから落下しないように円盤から正7角形をくりぬいてマンホールの蓋をつくる。
半径いくつ以上の円盤が必要か?落下に関して蓋の厚さは考慮しない。 >>7
考え方のアドバイス
もし問題が、「nを6以上の自然数、a,b,cを正整数のとき、a+b+c=n を満たす、(a,b,c)は何組あるか?」
だとすると、n個のボールを一直線に並べ、n-1カ所ある隙間のどこか2カ所に、仕切りを入れる方法は?
と読み替え、C[n-1,2]で求めることができる。
しかし、実際は、「a,b,c全て異なる」という条件と、「大小関係が指定済み」という条件がつく。
従って、いずれかの個数が等しい、つまり、a=b≠c、あるいは、b=c≠a、あるいは、c=a≠b、という場合と、
a=b=cの場合の個数をC[n-1,2]から引き、3!ので割れば、求められると考える。
a=b≠c の個数を求めるときは、nが偶数か奇数かで、分けなければならない。
a=b=cの場合の個数を求めるときは、nが3の倍数か、倍数で無いかで、分けなければならない。
従って、nを6で割ったときの余りで分類して解答を作ろうと考えるのが、常道。 >>7
根性で指折り数えてみた。指がたりなくなったので女子大生に手伝ってもらった(嘘)
n count
6 1
7 1
8 2
9 3
10 4
11 5
12 7
13 8
14 10
15 12
....
94 690
95 705
96 721
97 736
98 752
99 768
100 784 >>23(補足)
女子大生カウントを200まで増やして黒丸に、>11の数式を赤線にしてグラフを重ねてみました。

見事に一致しております。
女子大生カウントにミスはなかったようですw 証明がわからないときに具体例を計算するのは大変結構なことだが、
スレに書き込む必要はないよね
>>24
二次関数で最小二乗法で回帰させてみた
(n-1)(n-5)/12 + d_2 /4 + d_3 /3 = (1/12)^n2 - (1/2)*n + 5/12 + d_2/4 + d_3/3
> nls(Y ~ a*x^2+b*x+c, start=c(a=1,b=1,c=1))
Nonlinear regression model
model: Y ~ a * x^2 + b * x + c
data: parent.frame()
a b c
0.08333384 -0.50014021 0.66082814
residual sum-of-squares: 7.915997
Number of iterations to convergence: 1
Achieved convergence tolerance: 5.815117e-08
1/12=0.83333
1/2=0.5
5/12 + .... = 0.4166666667
上出来の近似 回帰式の値を四捨五入してみると
> data.frame(n,Y,round(Y.nls))
n Y round.Y.nls.
1 6 1 1
2 7 1 1
3 8 2 2
4 9 3 3
5 10 4 4
6 11 5 5
7 12 7 7
8 13 8 8
9 14 10 10
10 15 12 12
...
187 192 2977 2977
188 193 3008 3008
189 194 3040 3040
190 195 3072 3072
191 196 3104 3104
192 197 3136 3136
193 198 3169 3169
194 199 3201 3201
195 200 3234 3234
6から200まで、すべて一致している。
>>25
完璧な回答以外はいらないという話ならかなりの連中に刺さるんじゃないかな
>>8
以外の回答は蛇足で書く必要ないし 前スレが終わったと思ったら自称中学生のプログラミングジジイの知的障害者がスレ消費したのか
コイツをどこかに隔離しろよ
nを10以上の自然数とするとき
a+b+c+d=n, 0<a<b<c<d を満たす自然数の組(a,b,c,d)の個数をnの式で表わすことはできまつか。
1/((1-x)(1-x^2)(1-x^3)(1-x^4)をべき展開したときの(n-10)次の係数
はい、できます。
q_4(n-6) = (n-5)(nn-10n+13)/144 + (n-3)d_2 /16 - (d_3 - d'_3)/9 - d_4 /4,
ここに
d_2 = {1 + (-1)^n}/2 = (nが偶数のとき1, nが奇数のとき0)
d_3 = {1 + ω^n + (ω~)^n}/3 = (nが3の倍数のとき1, 他は0)
d'_3 = {1 + ω^(n-1) + (ω~)^(n-1)}/3 = (n-1が3の倍数のとき1, 他は0)
d_4 = {1 + i^n + (-1)^n + (-i)^n}/2 = (nが4の倍数のとき1, 他は0)
(大意)
この場合はd_2の係数がnの1次式なので、nが大きくなると振幅も大きくなる。
多項式回帰 >>23-27 は破たんの可能性・・・・ またまた訂正
d_4 = {1 + i^n + (-1)^n + (-i)^n}/4 = (nが4の倍数のとき1, 他は0)
制限付き分割数 q_k(n)
q_1(n)=1
q_k(n) = 0 (n<k)
q_k(k) = q_k(k+1) = 1,
これらは漸化式
q_k(n) = q_(k-1)(n-1) + q_k(n-k),
を満足して、生成関数
Σ[n=k,∞] q_k(n) x^n = (x^k)/((1-x)(1-xx)・・・・・(1-x^k)),
をもつ。
数セミ増刊:「数学100の問題」,日本評論社 (1984)
p.58
その次は・・・・
nを15以上の自然数とするとき
a+b+c+d+e=n, 0<a<b<c<d<e を満たす自然数の組(a,b,c,d,e)の個数をnの式で表わすことはできまつか。
1/((1-x)(1-x^2)(1-x^3)(1-x^4)(1-x^5)) をべき級数に展開したときの(n-15)次の係数
q_5(n-10) = ・・・・
pは3で割ると2余る素数とす。
どんな整数nに対しても n^2+n+1はpで割り切れないことを示しなさい。
宿題で出ました。教えてください。せめてヒントでも。
これまた有限体使うなら簡単だけど高校数学ではどうやるんだろうね
味噌も糞も一緒
プログラミングバカの一つ覚えは明日から味噌汁の代わりに糞汁を飲むかも知れない
>>40
もしp(=3k+2)|n^2+n+1ならnはF_pでの原始3乗根
しかしF_pの乗法群は位数が3k+1なのでそれは不可能 >>41
あ、そっか n^3 - 1 = (n-1)(n^2 + n + 1) か
ありがとう 有限体が使えるなら、こうやるか。
・p=2 のとき
nn+n+1 は奇数だから p=2 では割り切れない。
以下 p>3 は奇素数とする。
・n-1 がpで割り切れるとき
nn+n+1 = (n+2)(n-1) + 3 はpで割り切れない。
・n-1 はpで割り切れないが、nn-1 はpで割り切れるとき
nn-1=(n+1)(n-1) ゆえ、n+1 がpで割り切れる。
nn+n+1 = n(n+1) + 1 はpで割り切れない。
・n-1 も nn-1 もpで割り切れないとき
フェルマーの小定理から
n^(p-1) -1 はpで割り切れる。
もしも nn+n+1 がpで割り切れたと仮定すると
n^3 -1 = (n-1)(nn+n+1) がpで割り切れる。
∴ p-1 は 3の倍数となるが、これは題意に反する。
>>43
フェルマーの小定理使うなら場合分け意味なくてワロタ 〔フェルマーの小定理〕
n≠0 (mod p) のとき
n^(p-1) ≡ 1 (mod p)
だけど p-1 がこれを満たす最小の指数とは限らない。
・p=4q+1型のときは (-1)^((p-1)/2) ≡ 1 (mod p)
・・・・ 第一補充法則
・p=13 のとき
3^((p-1)/4) = 3^3 = 27 ≡ 1 (mod p)
>>46
もし最小の指数が分かれば、p-1はその倍数になる。
( n^r ≡1 (mod p) を満たす元 r の全体は F_p の乗法群の
巡回部分群をなす。) >>43 (追加)
・nがpで割り切れるときも
nn+n+1 はpで割り切れない。 >>46
(-1)^((p-1)/2) = (-1)^(2q) = 1 (p=4q+1)
= (-1)^(2q-1) = -1 (p=4q-1)
より明らか。 算数の問題ってどこで聞いたら良いですか?
よかったら0.9514の小数第3位切り捨てっていくつになるのか教えて頂きたいです
【ツイッター】「4-3=5+2」の棒を1本動かして正しい等式にせよ 小4が考案、数学者も悩ませた間題が超難問と話題 ★4 [ばーど★]
http://2chb.net/r/newsplus/1595603143/
941:不要不急の名無しさん 2020/07/27(月) 18:09:38.84 ID:lywT5IN20
>>939
無職の自己紹介ワロタw
943:不要不急の名無しさん 2020/07/27(月) 18:49:20.49 ID:lywT5IN20
と、無職 【愛知】草刈の作業員3人を次々とはね...27歳男逮捕 1人死亡「神様になりたかった」 [ばーど★]
http://2chb.net/r/newsplus/1595842064/
215:不要不急の名無しさん 2020/07/27(月) 18:43:14.58 ID:lywT5IN20
>>3
愛知の日常
頭沸いてる奴しか居ない
まともな奴は1割もいない
577:不要不急の名無しさん 2020/07/27(月) 19:00:42.91 ID:lywT5IN20
>>546
安倍が辞めたら、マシになる。国賊に権力握らせたから八百万の神が怒ってる
【愛知】クレーンで吊り上げた長さ4mの鉄板を掃除していたところ落下し下敷きに…工場で男性2人死傷 春日井 [ばーど★]
http://2chb.net/r/newsplus/1595838219/
520:不要不急の名無しさん 2020/07/27(月) 18:51:37.70 ID:lywT5IN20
>>1
愛知の日常 【ツイッター】「4-3=5+2」の棒を1本動かして正しい等式にせよ 小4が考案、数学者も悩ませた間題が超難問と話題 ★4 [ばーど★]
http://2chb.net/r/newsplus/1595603143/
947:不要不急の名無しさん 2020/07/27(月) 23:33:54.26 ID:MWTCSvAH0
と、負け犬
948:不要不急の名無しさん 2020/07/27(月) 23:34:46.19 ID:MWTCSvAH0
「等式」という言葉は中1で習う
等式に「せよ」という言い方は高校以上のものである
つまりこれは小4が作ったんじゃなく話題作りのためにオッサンが作った
はい完全勝利
頭空っぽのバカが嫉妬に狂って低能反論書き込みをしても
説得力まったくなし。皺・シミだらけの醜いマヌケヅラで書いてるんだろうなw
完全に俺の勝ちだなぁwww
950:不要不急の名無しさん 2020/07/27(月) 23:36:29.28 ID:MWTCSvAH0
と完敗したアホw 953:不要不急の名無しさん 2020/07/27(月) 23:40:09.19 ID:MWTCSvAH0
4-3=5+P
4-3=b+2
4-3=q+2
4-b=5+2
上の4つはPの方程式、bの方程式、qの方程式なので全部等式
幾らでも作れるよ
しかもオリジナルな正解もきちんと書いている俺、最強すぎ。
一方、非生産的なことしか書けないハゲ無職、あわれwww
954:不要不急の名無しさん 2020/07/27(月) 23:41:09.57 ID:MWTCSvAH0
バカはなにやっても勝てない
しょせんバカだからwww
956:不要不急の名無しさん 2020/07/27(月) 23:42:17.30 ID:MWTCSvAH0
頭悪いなあ
日本人じゃないのかもw
958:不要不急の名無しさん 2020/07/27(月) 23:45:00.34 ID:MWTCSvAH0
池沼がおぼえたての心理学用語つかってて笑える
しかも使うのも恥ずかしくなるような超基本的な用語www
用語だけ暗記しても就職はできないぞwww
960:不要不急の名無しさん 2020/07/27(月) 23:46:28.81 ID:MWTCSvAH0
おぼえたてのワードw
962:不要不急の名無しさん 2020/07/27(月) 23:47:45.79 ID:MWTCSvAH0
やっぱり池沼w
963:不要不急の名無しさん 2020/07/27(月) 23:49:45.26 ID:MWTCSvAH0
じゃもう一回書いておくかw
「等式」という言葉は中1で習う
等式に「せよ」という言い方は高校以上のものである
つまりこれは小4が作ったんじゃなく話題作りのためにオッサンが作った
はい完全勝利
頭空っぽのバカが嫉妬に狂って低能反論書き込みをしても
説得力まったくなし。皺・シミだらけの醜いマヌケヅラで書いてるんだろうなw
完全に俺の勝ちだなぁww
965:不要不急の名無しさん 2020/07/27(月) 23:52:14.45 ID:MWTCSvAH0
無職が何言っても説得力ないねえw
967:不要不急の名無しさん 2020/07/27(月) 23:56:35.16 ID:MWTCSvAH0
このおもちゃ、頭悪すぎてつまんなーいw
969:不要不急の名無しさん 2020/07/27(月) 23:59:47.70 ID:MWTCSvAH0
おっさん丸出しw
793:不要不急の名無しさん 2020/07/26(日) 15:55:02.46 ID:ZIc6sSfn0
>>791
知らないって書いてなかったら知ってることになるのかよ
高卒丸出しの馬鹿はいますぐ死ね低能w
こっちは大学教授だから。おめえ程度は社会的に抹殺できるからなw 【ツイッター】「4-3=5+2」の棒を1本動かして正しい等式にせよ 小4が考案、数学者も悩ませた間題が超難問と話題 ★4 [ばーど★]
http://2chb.net/r/newsplus/1595603143/
465:不要不急の名無しさん 2020/07/25(土) 10:33:34.32 ID:aSxhf2HF0
等式という言葉は中1で習う
つまりこれは小4が作ったんじゃなく話題作りのためにオッサンが作った。
469:不要不急の名無しさん 2020/07/25(土) 10:34:42.53 ID:aSxhf2HF0
オッサンの創作は絶対に許さない
永久に糾弾していくからそのつもりで。
498:不要不急の名無しさん 2020/07/25(土) 11:04:46.20 ID:aSxhf2HF0
>>493
大学教授だよ イナと同様のアホだからプログラムの人を非難するのは大いに同意するけど、プログラムそれ自体を高校数学外だからと否定する人は大学受験板に行けばいい
興味ないなら無視すれば良い
真面目にやってる人を非難するのは心が病んでる
こんなところでプログラミングをやってる池沼の方が心を病んでるだろ
正弦曲線を回転面でできたワイングラスを何度傾けたら半分のワインが残るか?

>>65
一辺の長さが1の正77角形の高さを手計算する?
普通、プログラム書いて数値計算するだろ。
そうでないなら計算式を書いてみてくれ。 >>63
じゃあお前は高校数学質問者がこの板に散乱しても良いとする立場を取っているって事で良いな?
大学受験板より数学板へ集まる状況下の中で高校数学質問者の招集隔離目的の
このスレの意義をそうやって頭っから否定するって事は。
「スレ持続運営力の意味の点だけ見ても力不足と言える大学受験板」の現実を無視して。
んなもん「高校生は大学受験板へ消えろ、コロナは余所で拡大しろ」と言っている様なもん。
お前1人がどうこう言ってどうにか出来る状況じゃないし呼応者も居ない。
お前1人がどうこう言ってどうにか出来る状況じゃないし呼応者も居ない以上、
このスレを質問を招集し隔離するスレとして継続していく方が万倍億倍賢明。
現実現状よりも独自理念を優先するのは実効が伴わなきゃ
程度の差は有れど「0.99999……は1ではない」説の安達や完全コピペ依存議論者のセタと同類。 >>63
いや別にお前が言ってる事は正しいぜ、一理あるぜ。
でも結局は「正義」なんだよ、個々人でぶつけ合う醜い方の「正義」。「自粛警察」と同類のゴミ。 A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれ同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
(脱字修正)
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
>>69
>67の問題は正何角形までなら、このスレの対象なんだ?
一辺の長さが1の正77角形の高さを手計算する? 1000pxの黄金比を求めるにはどうしたらいいのでしょうか。
片方が1、もう片方が1.618の割合になるようにしたいです。
>>74
その1000pxってどういう意味?
横が1000pxってことなら横1000、縦1618にすりゃ良いだけだよ
質問内容がよくわからない >>67
思った通りの知恵遅れだな
手計算で出せない問題は高校数学の範疇じゃないだろ
興味ある奴だけが専門板に行ってやればいいだけ
それくらい理解しろ池沼野郎 >>74
質問の意味がよくわからないが、比の問題は例えば
a : b = 1 : 1.618
にしたいなら
a / b = 1 / 1.618
を満たすように a と b を決めるだけでは >>75
1000ピクセルです
1000ピクセルを
1:1.681の割合に分割したいのです
縦横ではないです
横幅をです 学術の巨大掲示板群 - アルファ・ラボ http://x0000.net
数学 物理学 化学 生物学 天文学 地理地学
IT 涛d子 工学 言語滑w 国語 方言 など 1000÷2.681では?
373と627ならわりと黄金比
>>78
>>77は読んだ?
それなら a + b = 1000 として解くだけじゃね?
ちなみに整数解はないぞ >>78
そういうことか
じゃあ、1000を1/2.681と1.681/2.681に分ければいいんだよ >>77
そうですね その計算が良く分からなかったので、、、
>>81
なぜ2.681で割るんでしょうか?ロジックがいまいちわからない >>76
道具が使えないのはガイジ。
怒涛の計算力と根性があれば77角形の高さは計算できるぞ。
実際に答を書くこともできない池沼みたいだしね。
多分、>72もできない池沼認定してあげる。 >>76
あんたは高校数学でlog(2)を手計算していたの? 高校数学では
log(2) = 3010/9999
log(5) = 6989/9999
e = 2 + 71821/99990
なのだ。
これでいいのだ。
>>84
え?
>>77にどこか難しいところある?
わからないポイントがわからない >>84
x:(1000-x)=1:1.681 として方程式を解きましょうね
小中学校のスレは別であるからおうちに帰りましょうね~ >>76
1辺の長さが1の正何角形の高さの計算なら高校数学なんだ?
正777角形だと247.326になったけどあってるかw 前>>62
>>66ワイングラス満杯のワインの容積Vは、
V=∫[t=π/2→3π/2]π(3π/2-t)^2sintdt
=[π(3π/2-t)^2(-cost)](t=π/2→3π/2)-∫[t=π/2→3π/2](2t-3π)(-cost)dt 前>>92
>>66ワイングラス満杯のワインの容積Vは、
V=∫[t=π/2→3π/2]π(3π/2-t)^2sintdt
=[π(3π/2-t)^2(-cost)](t=π/2→3π/2)-∫[t=π/2→3π/2](2t-3π)(-cost)dt
=0+∫[t=π/2→3π/2](2t-3π)costdt
=[(2t-3π)sintdt](π/2→3π/2)-∫(t=π/2→3π/2)2sintdt
=0-(-2π)-2∫[π/2→3π/2]sintdt
=2π+2∫[π/2→3π/2](-sint)dt
=2π+2cos(3π/2)-2cos(π/2)
=2π
=6.283……
だんだんちっちゃくなるな。
なんでかな? こいつID:ck1YOXiH
マジで知恵遅れだろ
このレスを見れば分かりやすい
↓↓↓
>>86
> あんたは高校数学でlog(2)を手計算していたの?
log(2)の値を使う時は近似値0.3010が与えられて
手計算するのを知らない知的障害者
しかも>>76に3回もレスしてる
統合失調症の症状じゃないの? 中学を不登校で卒業した高校受験資格保有者にして未受験の引きこもりかもよ、
数2微積分も数1数列も習わない偏差値底辺高卒の可能性も有るけど。
中学校で全教科各20点以下しか取れなかった奴が卒業できる高校も存在する…。
まぁそれでバカの極み発言連発する奴でもコミュ障じゃなきゃ下働きなりに暮らしていけるんだろう。
このレスも頭が悪過ぎる
↓↓↓
>>85
> 怒涛の計算力と根性があれば77角形の高さは計算できるぞ。
77角形の高さってのがどの部分を指すのかは知らんが
怒涛の計算力がなくても根性なくても
手計算で近似値を出せる事が分からない知恵遅れ
1分も掛からないだろ
>>91
> 正777角形だと247.326になったけどあってるかw
正777角形の高さがどの部分を指すのか分からないが
同じく手計算で1分も掛からずに手計算出来る事も分からないキチガイ
バカは目障りだから消えろ >>96
一辺の長さが1の正三角形の高さは?
一辺の長さが1の正77角形の高さは? >>97
オマエがプログラミングキチガイか?
手計算で出せないとマジで思ってるのか? もうプログラミング絶対許さないマンに触れるのやめろよ
喧嘩売らなきゃ一人でブツブツ言ってるだけだけど触れるとこうなる
>>92
モンテカルロ法での値
6行でプログラム終わり
> wine <- function(x,z) -cos(sqrt(x^2+z^2))
> N=1e7
> x=runif(N,-pi,pi)
> y=runif(N,-1,1)
> z=runif(N,-pi,pi)
> (2*pi)*2*(2*pi) * mean(y >wine(x,z) & x^2+z^2<pi^2 )
[1] 18.44901

>>98
>>98 >>98
実際に出してないじゃん。
1分もかからんのだろ? >>99
オマエも正77角形の高さが手計算出来ないと思ってるバカなの?
高校数学をやり直せよアホ >>92
厳密解はこれ

∫[-1,-1] pi*(pi-acos(h))^2 dh = π(π^2-4) >72も手計算でできないはず。
少なくともあんたの頭脳じゃ無理だな。
>>101
マジで分からないのかよwww
じゃあ俺が正777角形の高さを1分未満で近似計算出来たら
オマエがこの板に二度と書き込まないと約束出来る? >>105
二度と書き込まないと約束出来る?
何なら正7777角形の高さを求めてもいいぞ >>108
あれ?急に条件厳しくなったなwww
怖じ気づいた? こっちを1分以内なら約束してもいいぞ。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
>>109
計算機に使って出した長さを手計算と嘘つくだろうから。 >>91
> 正777角形だと247.326になったけどあってるかw
あれ?小数第3位までしか求めてなかったよね
何で急に条件が厳しくなるのwww
ビビってるよなwww 道具が使えないのはガイジ。
怒涛の計算力と根性があれば77角形の高さは計算できるぞ。
実際に答を書くこともできない池沼みたいだしね。
多分、>72もできない池沼認定してあげる。
>>111
手計算で出せるって言ってるが分からないのか?
もし俺がきちんと手計算出来るって示せたら
オマエは二度と書き込まないと約束するなら教えてやるよ >>114
だから
怒涛の計算力が無くても根性が無くても手計算出来るって言ってるんだよ
ビビってるよね?
ビビってないなら二度と書き込まないと約束出来るよね? >>116
有効数字増やしてみた。247.32644462856607 >>117
有効数字を増やしてるwww
ビビってるよね cos(2π/77)の計算が必要になるから手計算じゃ無理だね
ID:a98DTw/Mは嘘つきである。
Q.E.D
>72は加減乗除だけだから、
三角関数の計算は必要ないから理論上は手計算できるし、計算式も書けるけど複雑すぎて手作業では無理だね。
>>118
プログラムの表示桁数を増やしただけだから、簡単。
手計算じゃないので。 2020角形だと、 高さ642.98545167655561
四則演算で出せるけど、これは手計算じゃ無理。
問題の内容は高校数学。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
>>119
ビビってるよね
有効数字を増やすのは条件の後出しだよな
>>91
> 正777角形だと247.326になったけどあってるかw
↑↑↑
俺はこの程度の近似なら手計算出来るって主張してるワケなんだが
ビビってないなら約束出来るよな?
俺が1分未満で手計算出来る事を示せたら
オマエは二度とこの板に書き込まない
そう約束出来るなら教えてやるよ >>121
> 2020角形だと、 高さ642.98545167655561
>
> 四則演算で出せるけど、これは手計算じゃ無理。
バカ丸出し
これも小数第3位か4位くらいの近似なら
1分も掛からずに手計算出来るんだがwww
俺は確率については一言も言及してないんだが
話題を逸らすなよカス >>119
> cos(2π/77)の計算が必要になるから手計算じゃ無理だね
バカ過ぎるわ
知恵遅れは算数からやり直せよ >>93
ワイングラスを傾けたときの3Dイメージを作ってみた。
単色だとわかりにくいので色を変化させておいた。
>>125
逃げてるwww
知恵遅れ且つビビりのチキンかよ >>93
傾けたときのワインの辺縁への中心からの距離がだせないので、いまだにモンテカルロ法での9.5°の答しかもっていない。

結局、数値を一度もかけないアホであることが判明。
こっちには言及すらできない、道具の使えないガイジ。
四則演算で出せるけど、これは手計算じゃ無理。
問題の内容は高校数学。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
>>127
あれ?何で約束出来ないんだ?
俺が手計算出来ないって思ってるんだろ?
それなら約束出来るよな
俺が手計算で1分未満で計算出来るって示せたら
オマエは二度とこの板に書き込まないと こういうのを書くひとこそ排除されるべきだと思うね。
>オマエは二度と書き込まないと約束するなら教えてやるよ
>>123
>俺は確率については一言も言及してないんだが
>話題を逸らすなよカス
俺も期待値にしか言及していないぞ。
話題を逸らすなよカス
話題を逸らすなよカス >>128
> 結局、数値を一度もかけないアホであることが判明。
明らかに逃げてるよな
オマエが約束したら示してやるって何度も書いてるだろ
さっさと約束しろよカス >>131
知恵遅れがビビってるなwww
カスは消えろよ 俺は、プログラム組んだから正n角値の高さを瞬時に計算させられる。
正11角形から19角形までの値
[1] 3.4775763858867372 3.7320508075688781 4.1178704772492472 4.3812862675348248
[5] 4.7571822271112918 5.0273394921258481 5.3958593286307917 5.6712818196177111
[9] 6.0341026397488760
数字も出せずにできるできるというのってスタップ細胞あります、に似ているなぁ。
>>129
手計算であった証拠がしめせないからね。
それ以前に数値すら示してないし。 こっちには言及すらできない、道具の使えないガイジ。
四則演算で出せるけど、これは手計算じゃ無理。
問題の内容は高校数学。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
>>131
文盲の知的障害者
>>119
> cos(2π/77)の計算が必要になるから手計算じゃ無理だね
> ID:a98DTw/Mは嘘つきである。
俺は手計算出来るって話をしてる
手計算に言及して
それを否定したのはオマエだろ
脳に欠陥があるなw >>137
数値も示せず、できるできるという道具の使えないガイジ。
四則演算で出せるけど、これは手計算じゃ無理。
問題の内容は高校数学。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。 >>138
約束すればいいだけだろ
キチガイが逃げてるwww プログラムなしでは事実上答がだせない、これには触れないみたいだな。
多角形の問題は簡単すぎて誰でもプログラム組めるけど。
計算機に計算させて手計算でやったと嘘をつけるしね。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
>>97
> 一辺の長さが1の正三角形の高さは?
お、お前た…ガガガ、○○○なのか?それを計算するのに必要な√3は暗記事項だろ?
更に開平筆算、開立筆算を習ってた世代の人達は暗記に頼らず開く事が出来る。辛いけど。
お前、中学で何してた? >>139
なんでそんな約束をする必要があんの?
手計算でできるなら、その計算式を書けばいいだけ。
書かないで条件つけているから、嘘つきと疑われる。
数値だけなら計算機に出させた値かもしれないし。
模範解答
77角系の高さの近似値は
24.506461149769844
になりました。
1分かからずに手計算しました。 >>140
話題逸らしに必死だな
俺は全ての問題が手計算出来るとは言ってないんだが
正777角形の高さについて計算出来ると言っている
>>91
> 正777角形だと247.326になったけどあってるかw
俺がこの値を手計算で1分未満で示す
それが出来れば
オマエはこの板に二度と書き込まない
こう約束すれば示すと何度も書いているんだが
逃げてるよな
ビビってるよな
ビビってないなら約束出来るよな >>141
>77角形の高さってのがどの部分を指すのかは知らん
というガイジへのレスだよ。 >>141(誤入力修正)
> 正77角形の高さってのがどの部分を指すのかは知らん
というガイジへのレスだよ。 >>142
たからきちんと手計算の方法を示してやるって言ってるんだよ
ビビってないなら約束出来るよな >>143
俺もできたよ。
77角系の高さの近似値は
24.506461149769844
になりました。
1分かからずに手計算しました。 >>146
こういうのを書くひとこそ排除されるべきだと思うね。
>オマエは二度と書き込まないと約束するなら教えてやるよ >>145
キチガイはオマエだろ
さっさと約束しろよ
そうしたらきちんと方法示してやる
何回言えば分かるんだよ知恵遅れ >>148
話題逸らすなカス
さっさと約束しろよ
ビビリのクズが >>143
汎用性がない方法なら要らん。
こっちも種類を変えても計算できる方法しか俺は興味がないね。
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。 >>151
汎用性とかwww
逃げまくりの知恵遅れのカス 円の面積や円周の長さから近似するんだろうな。
逆に7角系の方が誤差が大きくなりすぎるだろね。
>>152
おみくじ問題は分がわるいとみえて、逃げまくりw >>154
また話題を逸らす
いい加減にしろカス
全ての問題が手計算出来るとは言ってない
そもそも手計算出来ない問題は大学入試には出ないんだが
オマエは大学入試に関係ない死にかけの老害糞ジジイなんだろ
こんな所でしかマウントを取ろうとする知恵遅れ
ビビってないなら約束しろよカス >>152
数値を変えても答が出せるところにプログラム解の良さがあるんだよ。
こういうのも
容量8Lの袋と容量5Lの袋を使って池の水を5L集めたい。
袋に目盛りはついていません。
袋から袋への移し替えは全量で行います。
池からとる水の量や池に捨てる水の量には制限はありません。
最初に片方に満たした作業を1回目として
片方の袋に4Lを集めるのに最低何回の移動が必要か?
プログラムを組むと数値を変えて
40Lと39Lから20Lを図りだす76ステップが瞬時にだせる。
40Lから始めると78ステップ。 >>157
老害糞ジジイのキチガイ
話題逸らして逃げるクズ
ビビリすぎてお漏らししたか?
老人用のオムツでは穿けよw >>156
別に大学受験スレじゃないからな。
高校数学の範囲で理解できる問題を扱うだけで、その解法が限定されているわけでもない。
プログラム組んでいるから、多角形の作図とかすぐできるので、図形問題がでたときに考えやすい。

ワイングラスを半量満たした3Dは未だにきれいな図が描けないから、それができる人は尊敬するね。 >>159
話題逸らしに必死のお漏らし糞ジジイwww >>158
汎用性の話を実例を上げて解説しました。
道具の使えないガイジにはとうてい解決できない問題。
問題の内容は小学生でも理解可能。 >>161
約束出来ずに話題を逸らし続ける糞ジジイ
ビビってオシッコだけでなくウンコも漏らしたのか
まさに糞ジジイだな 今どき、グラフの作図手書きでなくてプログラムを使うだろ?
正弦曲線からなるグラスの描画は手書きじゃ無理。
>>163
逃げてる逃げてる
ビビって約束出来ずに糞尿漏らしまくりのキチガイ糞ジジイwww >>162
結局、数値を一度もかけないアホであることが判明。
うんこが好きだから、あっち系のひとかな? >>166
また逃げてる
約束すれば示すって何度も書いてる
約束せずにビビリまくりの糞ジジイwww プログラム命は高校数学質問生徒マウントレイプが楽しいのか?ホモなの?レズなの?バイなの?見境が無いの?
マウントとかいっているのは文明人でなくて猿だけ。
進化したボノボはそういう振る舞いはしないらしい。
1辺の長さ1の正7角形の高さの厳密解を求めたら
こんな式になってしまった。もっと簡単にできるかもしれん。
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
>>169
> 1辺の長さ1の正7角形の高さの厳密解を求めたら
> こんな式になってしまった。もっと簡単にできるかもしれん。
>
> (sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
まさに知恵遅れのバカだわwww 整備・整理・整頓・清掃・清潔・躾・習慣化の7S活動
>>169
ホカホカ相手が居ないお前は結局マウントレイプじゃん。汚物は消毒だ。 >>169
> 1辺の長さ1の正7角形の高さの厳密解を求めたら
> こんな式になってしまった。もっと簡単にできるかもしれん。
>
> (sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
高校数学を理解していればこんなバカな事は書かない
さっき中卒じゃないかという書き込みがあったが
実際そうかもしれないな >>173
プログラムがやっている計算を式に置き換えただけ。
んで、答あってる?
一度も数値を書き込めない道具の使えないガイジw >>174
またキチガイ出て来たよ
高校数学を理解出来ていない知恵遅れ
逃げてないで約束しろよ
ビビリの糞漏らしwww プログラミング知恵遅れは結局逃げたかwww
それとも老衰で死んだか?
>>169
> 1辺の長さ1の正7角形の高さの厳密解を求めたら
> こんな式になってしまった。もっと簡単にできるかもしれん。
>
> (sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
厳密解を求めてドヤ顔したつもりだろうが
バカ丸出しだと気付いていない知的障害者
数学Iの三角比さえ理解していれば求められる
それが分からないキチガイ
(1/sin(π/7)+1/tan(π/7))/2
これで求まるのによwww
(ラジアンは数学IIだが)
どんな計算をすればそんな複雑な式になるんだよwww
プログラミングで相手にマウントしているつもりだろうが、きっとマヌケなアルゴリズムを使って計算してるんだろうな
こんな単純な計算をパソコンで解こうとするから大恥をかく事になるんだよwww
二度と書き込むなカス 問題
一辺の長さが1である正七角形の高さを求めよ
高校生の解答
(1/sin(π/7)+1/tan(π/7))/2
プログラミング知恵遅れの解答
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
一辺が1の正7角形の隣り合う二つの頂点と中心を結んでできる三角形について考える
中心から正7角形の辺に対して垂直に補助線を引く
頂点と中心との距離
1/2 * 1/sin(π/7)
一辺を二等分する点と中心との距離
1/2 * 1/tan(π/7)
よって高さは
1/2 * ( 1/sin(π/7) + 1/tan(π/7) )
普通に解いたらあっという間だな
確かに何をどうやったら複雑な式になるのか分からない
こうすれば何か分かるかも
(
sin(2*pi/7)
/ ( (1-cos(2*pi/7))^2 + sin(2*pi/7)^2 )
- ( cos(4*2*pi/7)*sin(2*pi/7) )
/ ( (1-cos(2*pi/7))^2 + sin(2*pi/7)^2 )
- sin(4*2*pi/7)
/ ( (1-cos(2*pi/7))^2 + sin(2*pi/7)^2 )
+ ( cos(2*pi/7)* sin(4*2*pi/7) )
/ ( (1-cos(2*pi/7))^2 + sin(2*pi/7)^2 )
)
>>177
プログラムの式を出す出す方が遥かに難しいぞ。 >>177
プログラムのアルゴリズムを理解できてないじゃん。 sin(π/7)をどうやって手計算すんの?
テイラー展開は高校数学の範囲がだけど???
>>183
キチガイの負け惜しみwww
数学Iの知識で解ける問題なのに
そんな糞アルゴリズムを理解したいとも思わないがwww
>>184
正777角形の高さを手計算出来るとは言ったが
正七角形の高さを手計算で近似出来るとは一言も言ってないんだがww >>176
こういう計算してグラフを書かせる。
f <- function(n,print=FALSE){ # height of the polygon of side length 1
q=2*pi/n
r=cos(q)+1i*sin(q)
p=numeric(n+1)
for(i in 1:(n+1)) p[i]=r^(i-1)
H=abs(ifelse(n%%2==0,(p[1]+p[2])/2,p[1]) - (p[n%/%2+1]+p[n%/%2+2])/2)/abs(p[1]-p[2])
if(print){
plot(p,type='l',bty='l',axes=FALSE,ann=FALSE,lwd=2)
for(i in 1:n) segments(0,0,Re(p[i]),Im(p[i]),lwd=2,col=2)
}
return(H)
} >>186
すぐに劣等感に結び付けるキチガイwww
数学Iさえ理解していれば解ける問題を
プログラミングで解こうとする方が愚かだろ
プログラミング知恵遅れは数学Iすら理解していなかった
そんな奴がプログラミングで色々問題解いてドヤ顔してるのは滑稽だなwww >>187
そんな事しなくても数学Iの知識で求まるよなwwww
数学Iの知識すら無かった知恵遅れwww 数学がわからないとプログラミングが役に立たない例だな
数学がわからなければ計算機で出した「解」が正しいかどうかもわからないでしょう
どこにバグがあるかもわからないのに
どうやって解が正しいことを保証するんだか
やっぱり小中学生にはこのスレはまだ早いな
(a) 理論的に解くことが容易い問題
(b) 理論的に解くことは難しいが、計算機では解ける問題
(a)に計算機使ってることに疑問を呈されてるのに、反論に(b)を持ってこられてもな
>>190
実際にはCADを弄り回すだけでプログラミングなんてしない
バグがあったらそれはCADを作った企業の責任である こうすれば何か分からないかも…
(1/2) * ( 1/sin(π/n) + 1/tan(π/n) )
= (1/2) * ( (1+tt)/2t + (1-tt)/2t )
= (1/2) * (1/t)
= (1/2) * 1/tan(π/2n)
≒ n/π - π/(12n), (n:奇数)
>>66
モンテカルロじゃなくて計算機使ってようやく計算できた。
9.512676度傾ければ( ・∀・)イイ!! >>191
>72の後半、手書きでやってみ。カッコの対応間違えるから。 ブログラム信者に粘着する阿呆をスルーすればすべて解決
終
自演してるという半ば自供もあったしほんとにスルーするしかない
>>196
自演なんて指摘するとどうせまた暴れだす
スルーでいいよ 黒髭危機一髪みたいによくわからん原因で発生してくるんだよな
>>66
傾けた角度と残存ワインの割合をグラフ化

そもそも未成年者にお酒の話をするというのはコンプライアンス的にどうなのか
プログラムキチガイの格言
「プログラム組んでいるから、多角形の作図とかすぐできるので、図形問題がでたときに考えやすい。」
問題
一辺の長さが1である正七角形の高さを求めよ
プログラムキチガイの解答
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
>>203
数値あってるだろ。
どうせ計算は手書きじゃやらないし。
作図できたら長さや面積は数値積分でなんとかなるからね。
図形でなくてもプログラムは役に立つよ。
道具の使えないガイジには>72はできないようだけど。
俺は計算式まで出すようにプログラムできた。 >>202
こういうのもコンプライアンス上問題ある?
若い女性(嘘つきかどうかは不明)から
「あなたのいうことが正しければ手コキかフェラをしてあげる、そうでなければセンズリを命じる」と言われた。
フェラをしてもらうには何と言えばいいか?
尚、嘘つきであれば必ず嘘をつき、正直ものであれば決して嘘をつかない 問題
一辺の長さが1である正七角形の高さを求めよ
高校生の解答
(1/sin(π/7)+1/tan(π/7))/2
プログラミング知恵遅れの解答
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
プププw
>>207
>数値あっているだろ?
手計算できないの、ぷぷっ
>72からは逃亡中。 >>205
相手によっては質問をした時点でセクハラで訴えられるだろうな >>209
小学生に出すときはにはアメとチョコと腕立て伏せに変更だな。
因みにこの問題も道具の使えないガイジには答がだせないと思う。 >>205
いわゆる「嘘つきと正直者問題」を模倣したジョーク問題で、色々ガバガバすぎて問題としては成立していない。
せめて嘘つきでも正直者でもない人物の可能性くらいは想定した問題文でないと、まともな問題としてはお話にならない。 >>211
こういうの?
"
AからHの8人はそれぞれ正直者か嘘つきであり、誰が正直者か嘘つきかはお互いに知っている。
A,B,C,D,Eは嘘つきなら必ず嘘をつくが、F,G,Hは嘘つきでも正しいことを言う場合がある。
次の証言から確実に正直者と断定できるのは誰か?
A「嘘つきの方が正直者より多い」
B「Hは嘘つきである」
C「Bは嘘つきである」
D「CもFも嘘つきである」
E「8人の中に、少なくとも1人嘘つきがいる」
F「8人の中に、少なくとも2人嘘つきがいる」
G「Eは嘘つきである」
H「AもFも正直者である」
" プログラムキチガイ
「一辺の長さが1の正77角形の高さを手計算する?
普通、プログラム書いて数値計算するだろ。
そうでないなら計算式を書いてみてくれ。」
普通の高校生
手計算
(1/sin(π/77)+1/tan(π/77))/2
具体的な数値
→スマホの関数電卓機能で計算
所要時間30~40秒
プログラムキチガイ
こういう計算してグラフを書かせる。
f <- function(n,print=FALSE){ # height of the polygon of side length 1
q=2*pi/n
r=cos(q)+1i*sin(q)
p=numeric(n+1)
for(i in 1:(n+1)) p[i]=r^(i-1)
H=abs(ifelse(n%%2==0,(p[1]+p[2])/2,p[1]) - (p[n%/%2+1]+p[n%/%2+2])/2)/abs(p[1]-p[2])
if(print){
plot(p,type='l',bty='l',axes=FALSE,ann=FALSE,lwd=2)
for(i in 1:n) segments(0,0,Re(p[i]),Im(p[i]),lwd=2,col=2)
}
return(H)
}
とワザワザプログラムを組んで計算
高校生とプログラムキチガイ
どっちの計算が早いでしょうか?
プププw
>>212
ジョーク問題ではあるが>>205に比べると多少ジョークとしてのセンスはある。
しかしあくまでもジョーク問題であり、数学板としては板違いだと個人的には思う。
ちなみに内容としては「正直者は必ず正しいことを言う」と問題文に書かれていないことがポイントで
もし先入観でこれを思い込んでしまうと、どう考えても矛盾することになる。 >>66
y = -cos(x) -π<x<π の曲線をy軸の回りに回転させてできる面からなるワイングラスにジュースが満杯である。
極薄のストローを刺してジュースを半分飲んでいいと言われた。
満杯のときの何%の高さまで飲んでよいか?

尚、道具の使えないガイジには無理と思われる。 正直者は正直に答えるのが前提なので条件を追加。
"
AからHの8人はそれぞれ正直者か嘘つきであり、誰が正直者か嘘つきかはお互いに知っている。
A,B,C,D,Eは嘘つきなら必ず嘘をつくが、F,G,Hは嘘つきでも正しいことを言う場合がある。正直者は必ず正直に答える。
次の証言から確実に正直者と断定できるのは誰か?
A「嘘つきの方が正直者より多い」
B「Hは嘘つきである」
C「Bは嘘つきである」
D「CもFも嘘つきである」
E「8人の中に、少なくとも1人嘘つきがいる」
F「8人の中に、少なくとも2人嘘つきがいる」
G「Eは嘘つきである」
H「AもFも正直者である」
"
昨日のa98DTw/Mと今日のuMo8LokMでID検索してみたが、マジでこのスレだけに粘着してるのな。同一人物かはわからないが。
しかもまともなレスが1つもない。かまってちゃんここに極まれりということか。
プログラミングをやりたいならプログラミングのスレに行けばいいのに、ここに書き込むのが悪質
>>216
まずBが嘘つきと仮定する。Bの証言からHは正直者で、AとFも正直者となる。Cも証言が正しいから正直者となる。
正直者がA,C,F,Hの4人いるからAの証言が嘘になり、Aが正直者であることに矛盾する。
したがってBは正直者である。それに伴いCは嘘つきで、Eは正直者、Gは嘘つきとなる。
次にAが嘘つきと仮定する。Hの証言が嘘だからHは嘘つきである。
A,C,G,Hの4人が嘘つきであるが、Aの証言が嘘であることから嘘つきは4人以下であるので、残りのB,D,E,Fの4人は全員正直者となる。
しかしDが正直者だとFが嘘つきになってしまうので矛盾する。
したがって問題の設定が誤りである。
ジョーク問題としては成立していた>>212を改悪して答えの出ない問題に変えるとは。ろくなものではない。 >>219
途中が切れてしまってたから全文を上げなおします。
まずBが嘘つきと仮定する。Bの証言からHは正直者で、AとFも正直者となる。Cも証言が正しいから正直者となる。
正直者がA,C,F,Hの4人いるからAの証言が嘘になり、Aが正直者であることに矛盾する。
したがってBは正直者である。それに伴いCは嘘つきで、Eは正直者、Gは嘘つきとなる。
次にAが嘘つきと仮定する。Hの証言が嘘だからHは嘘つきである。
A,C,G,Hの4人が嘘つきであるが、Aの証言が嘘であることから嘘つきは4人以下であるので、残りのB,D,E,Fの4人は全員正直者となる。
しかしDが正直者だとFが嘘つきになってしまうので矛盾する。
したがってAは正直者である。
A,B,Eの3人が正直者であり、Aの証言が正しいことから残り5人は全員嘘つきとなる。
しかしCは嘘つきであるから、Dの証言が嘘であるためにはFが正直者となるため矛盾する。
したがって問題の設定が誤りである。 答がないようにプログラム組んで作ったからそれでいい。
一度、プログラム組むと条件に合わせて修正すればそれだけで答が出せる。人数を増やすことも可能。
このスレって「くだらねぇ問題はここへ書け」だったっけ?
小中学生の自作問題を投下するスレではないだろ
すみません
宝くじ板が荒れてるので助けてください。
1開催あたり1等の確率が480万分の1のくじについてです。
1000口買うのを50開催繰り返すのと
1開催で3万口買うのでは
どちらの方が一等当選の確率が高くなりますか?
>>225
前者だけど、買ってる口数がだいぶ違うんじゃ・・・?同じ口数なら後者が有利
・1000口買うのを50開催繰り返す⇒50開催で少なくとも1回以上1等があたる確率
1-(1-1000/4800000)^50=0.01036367505
1%ちょい
・1開催で3万口買う
30000/4800000=0.00625
0.6%ちょい こういうのって所謂ギャンブラーの誤謬とは違うの?
各開催で一等当選する確率は変わらないわけだけど
何度も買い続けると当たりやすくなるってなんか変じゃね
口数が違うのも気になるが
簡単にシミュレーションできる。
lot=c(rep(0,4800000-1),1) # 480万に1個あたりのlot
sim <- function(){
x=sum(replicate(50,sum(sample(lot,1000)))) # lotから1000口を50回買って当たった総数x
y=sum(sum(sample(lot,30000))) # lot から3万買って当たった総数y
x>y # x>yかを返す
}
mean(replicate(1e7,sim())) # 上記を1000万回繰り返してx>yの割合が0.5を超えるか確認する
結果はガイジが書くかもしれんw
極端な例で比較すると
1口を100開催買うのと50口を1開催買うのとで1等が1口以上当選する確率は前者の方が高いが、
1口を960万開催買うのと480万口を1開催買うのとで1等が1口以上当選する確率は後者の方が高い
どれくらいで逆転するかって話をしてるのかな?
なんかリボ払い的な思考に陥りそうで怖いな
一度にたくさん買う貯金はなくても、少しずつなら買える
→少しずつでも買い続ければ確率的にはそのうち当たる(?)
損得も計算に入れたら変わってくるのかな
コンコルド効果の実例って感じがするが
プログラム知恵遅れ
「一辺の長さが1の正77角形の高さを手計算する?
普通、プログラム書いて数値計算するだろ。
そうでないなら計算式を書いてみてくれ。」
普通の高校生が導いた計算式
(1/sin(π/77)+1/tan(π/77))/2
数学Iの三角比の知識のみで瞬殺
プログラム知恵遅れは数学Iの三角比が理解出来ていないので
わざわざプログラムを組まないと導けない
プププwww
つうか数学の問題として解くには情報が不足しているようなw
そこに気がつくかどうかだな。
>>232
プログラムで作図できれば長さも面積もプログラムで数値計算できる。正しい数値だっただろ?手計算で検算してないの?
道具が使えると>72も>215も答が出せる。
ガイジには無理だけどね。 2つの整数の和と差からの積は必ず一意の解が得られます。
和が奇数なら、積は最大値が矩形数で偶数の総和を減じて最小値は和から1を引いた数になります。
和が偶数なら、積は和の半分の2乗を最大値として、奇数の総和を減じて最小値は和から1を引いた数になります。
よって、和と積から差を求める問題には解なしという可能性もあります。
何故そうなるのですか?
>>236
>2つの整数の和と差からの積は必ず一意の解が得られます。
和a=m+nと差b=m-nから積c=mnを求めるということか?
c=(a+b)(a-b)/4 だから、m,nが整数という条件のもとではcは一意に求まるわな。
>和が奇数なら、積は最大値が矩形数で偶数の総和を減じて最小値は和から1を引いた数になります。
>和が偶数なら、積は和の半分の2乗を最大値として、奇数の総和を減じて最小値は和から1を引いた数になります。
和 a=m+n が一定のとき c=mn=n(a-n)=-{n-(a/2)}^2+(a/2)^2 だから
aが奇数のときa=2k+1とすると、n=(a±1)/2,m=(a∓1)/2のとき最大値c=(a^2-1)/4=k(k+1)
aが偶数のときは、n=m=a/2のとき最大値c=(a/2)^2
ということを言いたいのだろうな。しかし最小値は存在しないぞ?負の整数を忘れていないか?
>和と積から差を求める問題には解なしという可能性もあります。
和a=m+nと積c=mnから差b=|m-n|を求めるということか?
b=√(a^2-4c) だから、m,nが整数という条件のもとではbは一意に定まるはずだが。
もしかしてm,nが整数という条件を外しているのか?a,cが整数という条件だけではbは整数となるとは限らないぞ。
>>236に書かれている3つのことの理由を説明すると以上のようになるわけだが、この3つのことには何の関連性もないぞ。
総じて全体的に意味がとても取りづらい文章なんだ。まず日本語を数式化してくれ。
なにか数学的な現象について考えるとき、とりあえず数式で表してみるというのは基本中の基本でありまず最初にやるべきことだ。
たったそれだけで解決することも多々あるからな。こうもわかりにくい文章で書かれるとそれだけでやる気がぐっと減衰するというものだ。 f'(x)をf(x)で、あるいはf(x)をf'(x)で微分するときって、
f(x)の具体的な式が指定されていない場合どうすればいいのでしょうか?
df ' / df = df ' /(f ' dx) = f " / f '
df / df ' = (f ' dx) / df ' = f ' / f "
てな感じで・・・・
>>235
何こいつ?
数学Iの三角比すら理解していない池沼なのに、未だにマウント取ろうとしている。
やたら道具道具を連呼しているけど、数学Iを理解してない池沼ですら使える道具を自慢されてもな。
>1辺の長さ1の正7角形の高さの厳密解を求めたら
>こんな式になってしまった。もっと簡単にできるかもしれん。
>
>(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
道具に頼る事しか出来ないからこんな間抜けな式を書いてドヤ顔する事になる。 >>240
正しい値だろ。
1分以内に手計算終わってないのか?
道具が使えると>72も>215も答が出せる。
ガイジには無理だけどね。 宝くじの問題
10分の1で10万円が当たる宝クジAと1万分の1で8000万円が当たる宝クジBがあるとする。
宝クジ1本の値段は前者は2万円,後者は4万円とする.
購入金額100万円としてどのように買うとき賞金の期待値が最大になるか?
>>241
本当に頭が悪いんだね。低脳過ぎるよ。
>こんな式になってしまった。もっと簡単にできるかもしれん。
こんな馬鹿な事を言っちゃうような池沼爺。
数学Iを理解していれば
(1/sin(π/7)+1/tan(π/7))/2
こんなシンプルな解答が出せるのに。
みんな思ってるよ「こいつは数学Iすら理解出来ていない池沼爺」だって。
道具に頼ってばかりだから単純な問題さえまともに答えられない。 別スレの問題をやってみた。
問題の意味は高校数学の範囲。
分からない問題はここに書いてね461
http://2chb.net/r/math/1594131967/824
824 名前:132人目の素数さん[sage] 投稿日:2020/07/31(金) 06:02:41.54 ID:EiI9yUPg
AB=4,BC=5,CA=6の△ABCの周および内部の領域をDとする。
D内に以下の条件を全て満たすように2つの正方形SとTを配置したい。
Sの一辺の長さsを求めよ。ただしTの一辺の長さをtとすると、s≧tである。
(i)SとTはともにDに含まれる。
(ii)SはTの外部にあるか、またはSとTは外接している。
(iii)条件(i)(ii)を満たすS,Tの配置は様々であるが、その中で積stが最大である。
道具を使って解いてみた。

道具の使えないガイジは手計算で正解がだせるのかな?? >>243
プログラムで作図できれば長さも面積もプログラムで数値計算できる。正しい数値だっただろ?手計算で検算してないの?
道具が使えると>72も>215も答が出せる。
>244を手計算でやって頭がいいのをみせてくれて!
ガイジには無理だけどね。 ID:qORrAykd = ID:6WqfoPjj か
自演乙
プログラム池沼爺がまた出て来た。
昭和生まれの老いぼれ池沼爺が高校生に
「お前ら車の運転出来ないの?」
とマウントするようなもの。
徒歩だと30秒で行ける距離すら車で移動する池沼爺。しかもかなり遠回りしている。
更に、東京~大阪間を車で移動して
「お前ら大阪まで徒歩で来れる?」と言っているような感じ。
知恵遅れと呼ばれているのも納得出来る。老害は生きている価値が無い。
>>247
水洗トイレとトイレットペーパーがあるのに
野糞が一番と言っている道具を使えないガイジだなぁ
>72に手計算でサクっと答を出せればあんたの好きなマウントとれるぞ。
今日中には正解は出せないと思うね。 >>248
的外れな返しだな。高校数学でプログラミングはやらないんですけど。習っていない事が出来なくても全く恥ずかしくない。
それに対して池沼爺は数学Iの三角比が分からなかった。これはかなり恥ずかしい事。それなのにまだこの板に常駐出来るとは。
それに、ここは出題スレではないんですけど。誰1人そのクソつまらない問題に興味示してないのが分からないのか?池沼爺は邪魔。死ねば? このスレでは高校レベルの知識以外は出してはいけない、というルールにするのかな
今までは大学での知識も使っていたけれど、それへの批判は特になかったように思うが
プログラムだとなぜ駄目になるのか
そのプログラムを使っている人の問題はあるかもしれないが、プログラムが駄目ってのは論理的にどう説明されるんだろう
マウント批判に対して、
「自分が出題した(ナンセンスな)問題を解けばマウントがとれる」
とはあまりにもナンセンスな返し
論理の基礎(数学A)すらわかってなさそう
>>251
>244は別スレの別人の問題。
サクっと手計算で答えれば好きなマウントがとれるぞ。
>72はコレクター問題の拡張だし、ワイングラスの話は積分で別に
ナンセンスな問題でもないよ。 >>250
例えば、パソコンを使わないと数値計算出来ない積分は明らかにスレ違いだろ。池沼爺が出題していたワイングラスの容積とか。
ワイングラスの容積だけなら逆三角関数を知っていれば手計算で出せるだろうけど。 >>252
この池沼爺はID変えて自演してるよな。バレてないと思ってるのか? 横からだが
プログラミングは人類の重要な道具だし、それを使って解くべき問題も無数にある
しかしこのスレにおいてはどちらかというとスレチだろうね
>>253
今までの慣習でいけば、質問者が高校レベルで解けるかどうかまで含めて質問とするケースなど問題自体が高校レベルでない場合も許容されてきていたから、そのスレ違いの感覚が分からない
プログラムが問題なのではなく、出題された問題が高校レベルがどうかが問題ということ?
私はプログラムなどは許容してもいいし、単にその人が不必要な煽るレスで荒らすことが問題だと感じてる
だからプログラムだからという理由付けで批判しその人へ煽り返す人も今までの慣習との整合性がなく荒らしに見えるんだ 数値計算が必要になる問題や大学数学の問題を高校数学風に装って出題してる奴いてるよな
>>245
>プログラムで作図できれば長さも面積もプログラムで数値計算できる。
この池沼爺は正多角形の長さや面積をプログラムを組まないと求められないのか。
高校数学では三角比を使って表現出来ればそれで十分。具体的な数値を求める意味はない。何かを設計しているわけじゃないのだから。
数学Iすら分からなかった池沼爺が何を言っても無駄だね。 >>250
(1) 聞かれてもいない「プログラム解」は数学的な正当化がない限りは「数学的な解」にはなりえない
(誤差の議論がない浮動小数点数の計算は論外)
(2) 聞かれてもいないプログラムのソースを書くのは明らかに板違いで邪魔
(3) 聞かれてもいないプログラムの膨大な出力結果は邪魔
例えば、
「数値計算するとこうなったんですが、数学的には解けますか?」とか
「プログラム書いて計算したらこんな式が成り立つのではないかと思ったのですが、証明がわかりません」
とかならまだ意味があるが、
「こんな問題考えたぜ!お前ら解いてみろ」とか
あまつさえ自分が出題した問題を自分で解くとか、そういうのはただの荒らし
要するに使い方の問題
使う人がダメだとツールがダメに見えるのも当然の話 >>252
>マウント批判に対して、
国語の勉強から始めようか >>259
そう使い方の問題
解けない問題が質問された場合にシミュレートしてみることなどは有効だから、不要なものではない
そこに書いてあるようなものが荒らしであることには全く異論がないが、今までの慣習と整合性のない意見が強い口調で書き込まれてるから気になってる
あと数学やる人間として、ツールが駄目に見えた、だからツールは駄目だという主張はいかがかと思う
使う人とツールは関係がない >>256
池沼爺は最初からプログラムで解くことを前提に自分で出題して自演している。
単にプログラムを組める事を披露するのが目的。
それなら最初から専門板に行けばいいだけの話。このスレでは邪魔なだけ。 >>262
日本語を読んでほしいのだが、私が批判しているのはプログラムをスレ違いとする意見にだ
彼が荒らしでないなどとは言っていない >>261
シミュレートするのは自由だが、ほとんどの場合このスレに書き込む必要はない
(質問者が望んでいない限り)
>使う人とツールは関係がない
それは一般論ではそうかもしれないが、少なくともこのスレでは害悪でしかない
なぜなら、有効活用されていないから
>>259の(1)に書いたが、数学的な正当化がなければ数学的には無意味
そのような正当化や誤差の議論を含む回答は見当たらないので >>264
それは彼個人の問題であってプログラムの問題でないように思う
406全てのログを漁るわけにも行かないのだが、一度も役に立ったことがないのだろうか? >>265
>406全てのログを漁るわけにも行かないのだが、一度も役に立ったことがないのだろうか?
それは知らない
プログラムを使うのは自由だが、少なくとも「プログラムを書いたらこうなりました」はスレチ
>>259に書いたような使い方ならおk >>263
俺だってプログラミングを全て否定している訳ではない。
例えば、「この定積分を求められますか?」みたいな質問で、不定積分が初等関数を用いて表せないならパソコンで数値計算するのもありだと思う。
しかし、あの池沼爺はプログラムで解くことを前提に出題している。明らかにスレ違い。 もう離れるが、冷静になって彼が荒らしであることとプログラムの問題は切り分けて論じてもらいたい
プログラムは他の高校より上のレベルの数学と同様に数学の道具として有用なものなんだ
プログラムだからスレ違いのような意見は今までとの整合性がないし、荒らし批判のためなら整合性がなくてもいいわけでもない
荒らし批判したいなら荒らしとしての特性を批判すればいいだけだ
高校数学以外は何も出せないような息苦しいスレにならないことを祈る
>>268
プログラム自体を全否定している奴はいないと思うけどね。 小学生につるかめ算教えようとしてるときに、連立方程式で教えようとするのは全く意味ないですよね
プログラムはそれと同じなんですけどー
このスレ数学板の他のスレと比べて明らかに頭悪いからまともなこと言ったって理解されないのにご苦労なこった
クソガキがしょうもないレスしてうぜぇから隔離してんだよ
クソガキの自由にやらせておけ
確かにマウントとりにいったり取られたことを気にしたりする人もいます。
しかしROMってる大半の人間は、高校数学より上の知識に敬意を持っているし、また高校数学の知識しかない人を貶めようとも考えてません。
声がでかい人がマウント合戦しているだけなのを見てスレ全体を決めつけないでほしい。
このスレでのプログラム爺がお客様というより、この板での高校数学という名の算数縛りがお客様だよなぁ
算数しかしたくないなら他所いけよ、なんで数学板にこだわるの?数学する気はないくせに
>>273
「高校数学の質問スレ」なんだから別に構わないのでは はっきりいって、このスレ閉じれば済む話
誰も学問としての数学的観点から高校数学への解答なんて求めてなかったんだよ
その板に高校数学質問スレを作ることが間違いだった
いやしかし高校生が数学の質問したいとかいって勘違いして数学板に来てしまったときの隔離スレは必要なんだよな
そういう頭の悪い高校生を隔離するうまいスレはできないか?
>>276
このスレでしっかり高校数学以上の知識で殴ってあげればいい
お前らのやってることは算数だぞと教えてあげるスレにしよう ↑
汚い言葉使って印象操作が酷いな
数学板で数学的手法使って数学の問題に答えて何が悪いんだ
数学してない連中の隔離スレなんだから隔離された連中が悪いに決まってんだろ
嫌なら別板いけ
高校数学が算数であることは確かだが、
だからといって高校数学の範囲内で解ける問題をそれ以上の知識を使って解くのはナンセンス
(大学生以上ならほとんど成人以上だろうが、まさに「大人げない」)
大学レベルのエレガントな証明を紹介することは悪いわけではないが、
ほとんどの場合においてただの自己満足でしょう
>>270
中学数学板に鶴亀算スレ立てたようなもんだな
連立方程式来ないと思ってるほうがアホ 大人が混ざってる日本に小学校立てたら、その中では小学生の勉強するんですけど??
なんで小学校で中学の勉強やっていいことになるわけですか?
>>281
それはどうかと
高校数学が算数であるという主張の中にある、数学でないという意味、学問でないということがどういうことなのか理解しているか?
数学は別に高校数学をより応用したものではない
>>283
比喩が間違っている
数学板とは数学のみを扱う板であって数学も扱う板ではない
でなければあるいは、このスレは高校数学だと銘打ってはいるがその中には高校生以外も色々いるから何でも扱っていいという話になる 今年はコロナのせいで夏休みは短縮されてるはずなんだがなぁ
夏か
>>284
いい歳をした大人なら、質問者のレベルに合わせて回答できるよね
それをしないのは「大人げない」って話
板違い云々の話なら、このスレは高校生用の隔離スレなんだから的外れだし ここはジャンル学問の数学板です
理解できない方はマウント取られた!とか言う前に適切な板に移動お願いします
子供が言いがちなこと
大人なんだから大人らしく振る舞え!
俺たちは子供だから子供らしく振る舞うけど!
クソガキの隔離スレがあってよかったが、なんで隔離されたクソガキの分際でこんなに威勢がいいんだろう
邪魔だから仕方なく隔離されたのであって、隔離スレのルールなんて知らんよ
嫌ならよそいけよそ
>>290
今の議論は、(君の言う)隔離された人たちが文句言っているわけではないと思うけど >>289
>>290
まず隔離されてる時点で話題が板違いで問題があることを自覚して大人の対応してほしいわな
自分たちが来る板が間違ってるということは頑なに認めないのかな 高校数学の質問を計算ソフトで答え茶化すスレ
にしてくれてんじゃねーよプログラムカンニング野郎が
最近はもうスレごとに高校生のあらしが来るな
パートいくつからこんなことになったんだ、だから質問以外高校生にさせるなって言ってるんだ
マウント合戦、的はずれな回答、高校数学以外は許さない、etc
まともな高校生なんてほぼいないし、何ならここにいる高校生の9割はここにいる「大人」の数学力に届かずに生涯を終えるのに
しかし今日はやたらIDが多いな
こんなにROMってたのか
おまえら論理の基礎である数学A(笑)を勉強しろよ~
こんなもんで論理は基礎付けられてないとかいう正論はやめろよ~
>>289
子供のそれ、リアルなら子供だなぁで済ませるけど、こういう匿名掲示板でやられるとさすがにな
親からネット禁止してもらわなきゃ駄目だろって思うわ 自分では自演しつつ、相手が自演しだしたら自演乙!というのがプログラムスンナ派のやり方
スンナ派も自演してるやつがいるのにね
良識派(論理関係重視派)は自演の指摘なんてなんの正当性にも結びつかないからやらないということに甘えて優位に立とうとしてる
「俺以外にも自演してる奴いるんだから良いじゃん!」
>>302
こういう自演とかいう些末なことだけ指摘して論理関係黙ってること害悪なんだよな
論理関係すべて指摘したあと暇ならやることだわ >>302
まさに非難されてるクソムーブかましてて草
日本語読めないのかな いやガキはここを数学板だと理解してないガキとそのガキであるお前が指摘する荒らしな
プログラムは関係ない
夏だなぁ
なんで数学が分からないくせに数学板に乗り込んできて数学やるななんて言うんだろう
>>304
スンナ派に自演してる奴がいることと自演を指摘することに関係がないと言ってるんだが
日本語読めないのかな 別に数学板的にはこのスレが荒廃しても存在してれば誘導できるので問題ないんだわ
あとはバカな高校生たちがプログラム許さないもん!数学ゆるないもん!って言ってこのスレを荒廃させるか、まともな「数学」的意見を参考にしたいかだけ
ただ一つ言えるのは、高校数学とかいう算数を扱うスレにはならないよ、板違いだから
そんなマウントと取られちゃうこと言っちゃ駄目だよ
子供は大人にとっての常識を理解してないから、それを見せられるだけでマウントととっちゃうんだ
本当は大人の世の中はマウントではなく論理で出来てるんだってことを10代では理解できないよ
>>302
婉曲表現で論理性を表現するとは素晴らしい
文学が似合っている >>311
で、スンナ派に自演してる奴がいることと自演を指摘することにどうして関係があるの? 大人しく質問して、回答してさえいればよかったのに
変にプログラムだからスレ違いみたいな変な意見出した連中のせいで荒れてしまった
嵐は嵐として対処すればいいのであって、プログラムはスレ違いみたいな変な論理なら指摘されるに決まってるだろう、数学板だぞここは
嵐にはマウントとって強い言葉で攻撃してもいいなんて他板の愚行が通じるわけ無いだろう……
>>313
そのレスバは勝敗が決まったあとになにかこのスレにとって役に立つ意見が出るのか
立たないからやめろよ煽りたいだけの荒らし レスバしたい人帰って
ホント邪魔
お前以上の嵐はいない
レスバいいでしょこのスレはクソスレだから
荒らしも容認するって意見なんでしょ
一体何人が同一人物で、何台のマシンをつかっているんだか
こんな過疎スレに「IDが変わる環境」で書き込んでいるやつがそう何人もいるわけないだろ
>>319
まあ気にするな
普通の感覚なら>>259が結論でほぼok
どのみち5chで自治は無理だから言い争わず放置が最良 中学生が夏休みに入ったのかね
ここは高校数学の質問スレだが
もうこのスレレスバ遊び場にしよう
どうせ数学の話するとマウントなんて言い出して暴れる人間がいるんじゃ機能しないよ
>>322
そうだよ
>>259
こんな数学と荒らしかどうかの話の切り分けもできない連中がいるんじゃ自治なんて無理 >>323
さすがに中学生は来ないだろう
高校生では? >>326
さすがに高校生ならここまで幼稚じゃないと信じたい >>327
貴方も幼稚な荒らし筆頭の一人なんだけど……
最初から理詰めで指摘すればいいのに自演乙とか煽ったりさ
ここをニュー速か何かと思ったのか? 普通の感覚なら
ID:ke/J+KMF
が結論でok
煽るような言葉遣いしてる連中なぞ全部嵐で終わり
>>324
いいね
マウントザルになって自演しつつ相手の自演叩いてドヤ顔になろう
そういうスレらしいからね プログラム使う荒らしを指摘したかったんだよね
そこをうまく表現する力がなくプログラムが攻撃対象であると取られるような表現をしたり、煽り返したり、そして自分が正しいのだという様子で冷静な意見にも反論したりするのだからまぁお前も嵐だろと言われるのは当然かなといったところ
スレがこんなになっちゃうのはこっちにとっても迷惑なので、それでも自分の過ちを認められないというのは残念だ
>>331
話聞いたなかったの?アホどもは高校数学以外は百歩譲っても必要最低限しか見たくないって言ってんの
数学やる気が無いんだよ
だからスレ違いだの高校数学の範囲だのという話が出るの
本来数学の話するときにそんなもん関係ないに決まってんのに >>309
その論法が通るなら
別に数学板的にはこのスレが荒廃しても存在してれば誘導できるので問題ないんだわ
あとはプログラム気違いが高校数学許さないもん!質問ゆるないもん!って言ってこのスレを荒廃させるか、まともな「数学」的意見を参考にしたいかだけ
ただ一つ言えるのは、プログラミングとかいうカンニングを扱うスレにはならないよ、板違いだから
と言う主張も通るし高校数学を算数呼ばわりするのは昔からよくある過言 >>333
プログラミング気違いってこのスレで意見を参考にしたかったのか……
プログラミング気違いはこのスレが荒廃しようとほんとにどうでもいいと思うぞ
自治したい人たちがこのスレをどうしたいのかだけじゃね 今日の献立から専門的な話まで、が本来のチャットの存在意義であり
プロが玄人顔で素人がする話題や質問を除け者にするのは日本含む極東アジアの傲岸不遜な悪癖で
高校数学を算数呼ばわりするのは其の典型例
素人の話題が除け者にされたっけ?
一部の回答は玄人としてのけ者にされたけど
>>335
評価が別でなされてるものに比喩して印象操作するのは詭弁の一つ
意見を否定しないけどそんなことする人を信用できない >>333
よっしゃこのスレ荒らそうぜ!
論法が通らないことの反論がないってことは荒廃してもしかたないってことだろ!
はっきり言ってお前のそれは屁理屈だけど荒廃させるなら仲間だぜ! 単発軍団、嵐は嵐だけど意味不明なこと書きなぐるのではなく論理性をしっかり持たせてくるの笑うわ
このスレ好きすぎるだろ
>>334
参考オナニーしたいからプログラミングマウントレイプしに来てるんだろ
>>336
高校数学を除け者にしようとしている奴が昔からいるじゃないか
>>337
その評価、フレキシブルだな。金さえ積みゃあ言うこと変える評論家だな >>341
お前どこからそんなモチベーション出てくるの? >>340
【悲報】詭弁はフレキシブル
ありがちな詭弁使っておいて、詭弁が論理的に研究されてることも知らないのか…… >>333
高校数学では数学の問題をプログラミングで解く方法は習わないんだから
プログラミングはカンニングじゃなくて単にスレ違いだと思う >>338
判断が拙速だな。早漏か?俺は遅漏だから待てよ。買い物に出掛けたいのに。
別に早い内に捲し立てて逃げ勝ちする手口をやりたいわけじゃないだろ?
例を変えて通らない論法なんざ飾りに過ぎねぇよ。
極端な例に変えられても通用する位じゃなきゃ。例えば
「嫌よ嫌よも好きの内」や「好きの反対は嫌いじゃなくて無関心」な。
「じゃあ嫌いな糞を食ってみろ。嫌よ嫌よも好きの内なんだろ?」とか
「じゃあノコギリでお前自身の腹を切れ。好きの反対は無関心なんだろ?」と言ってやれば良い。 そういやBASICってまだ高校数学の教科書に載ってるのかな
思えば数値を出すだけならあれで十分いいんだよな
>>347
関数電卓使う不正の延長みたいなもんだ。ラベリング的にカンニングだろ。 煽ったら勝ちだから
今はプログラム爺が荒らしてるのでとりあえずプログラム爺叩きに乗れば勝ち
>>352
関数電卓の使い方も高校の時は習わなかったと思う
工業高校だと習うのかな いや荒らしてるのはどちらもだろ
さすがに荒らしがプログラムシーヤ派だけってのは通らんわ
>>347
私の意見を読んでこれまでのこのスレの流れとの整合性について教えてほしい 機械電気建築自動車etc授業中の問題で関数電卓、ポケコンを使うんだろ
>>359
だよね
プログラミングは大学数学のように単に高校数学の範囲外なのであって
このスレは試験じゃないんだからカンニング=ずるいというのは感覚的におかしいと思う 1. プログラミングはやめろを発見
2. プログラミングは使い様によってはOKだろと投稿
3. プログラミングがOKなら大量に投下するアホ発生
4. アホな投稿やめろ
5. OKなので引き続き大量に投下
6. アホがおるのでプログラミングはやめろ
7. 1に戻る
2と3はとりあえず繋がらないかな
アホはプログラムがokでなくても投下するんだからね
プログラム禁止という変な方向に誘導してしまうような表現はちょっと
荒らしがいるというその一点だけが問題なんだから
コレクター問題の発展版
A~Jまでの10種類のおみくじが全部で55枚ある。
その枚数はA:1,B:2 C:3 D:4 E:5 F:6 G:7 H:8 I:9 J:10枚である。
おみくじが引かれたらそれと同じ種類のおみくじが補充される。
10種類全部を集めるために必要なおみくじを引く回数の期待値を求めよ
枚数がそれぞれa,b,c,d,e,f,g,h,i,jであったときの期待値の計算式を記載せよ。
a,b,c,dを実数としてf(x)=x^4+ax^3+bx^2+cx+dとおく
xの方程式f(x)=0が異なる4つの実数解をもつとき、
任意の実数kに対して、
xの方程式f(x)+kf'(x)=0も異なる4つの実数解をもつことを示せ。
知り合いは「まあグラフ考えたら明らか」とゆうんですが私には全然わからんです。
それにこの問題で「グラフ考えたら明らか」と答案に書いても減点されますよね。
>>366
f(x)=(x - p) (x - q) (x - r) (x - s)として
f(x) +kf'(x)=
(x - p) (x - q) (x - r) (x - s)+
k(x - p) (x - q) (x - r) + k(x - p) (x - q) (x - s) +k (x - p) (x - r) (x - s) + k(x - q) (x - r) (x - s)
これを微分してグラフを考えれば良さげ。 >>367
p<q<r<sとしてF(x)=f(x)+kf'(x)で
F(p),F(q),F(r),F(s)の正負を考えればいいからF(x)を微分する必要もないな。 >>366
f(x) = 0 の異なる4つの実数解を p, q, r, s とするとき、
F(x) = f(x) + kf'(x)
において F(p), F(q), F(r), F(s) の符号を調べれば中間値の定理が使えそう >>366
f(x)=0 の4つの実数解を小さい順にα,β,γ,δとすると
f'(α)<0,f'(β)>0,f'(γ)<0,f'(δ)>0 となるのはf(x)のグラフからわかる。
g(x)=f(x)+kf'(x)とする。
k=0のときはg(x)=f(x)だから異なる4つの実数解をもつことは明らか。
k>0のとき
g(α)=kf(α)<0 , g(β)=kf(β)>0 , g(γ)=kf(γ)<0 , g(δ)=kf(δ)>0
これらと lim[x→-∞]g(x)=∞ から4次関数g(x)のグラフを考えると
4つの区間 (-∞,α),(α,β),(β,γ),(γ,δ) にそれぞれ1つづつ解をもつことがわかる。
k<0のとき
g(α)=kf(α)>0 , g(β)=kf(β)<0 , g(γ)=kf(γ)>0 , g(δ)=kf(δ)<0
これらと lim[x→∞]g(x)=∞ から4次関数g(x)のグラフを考えると
4つの区間 (α,β),(β,γ),(γ,δ),(δ,∞) にそれぞれ1つづつ解をもつことがわかる。
その知り合いとやらが言いたいのはおそらくこういうことだろう。
実際に答案を作成するなら中間値の定理とかも含めてもっと詳細を丁寧に記述するんだぞ。 >>370
申し訳ない。表記ミスがあった。
k>0 のときと k<0 のときの
kf(α) , kf(β) , kf(γ) , kf(δ)
に全部ダッシュを付け忘れていた。
k'f(α) , k'f(β) , k'f(γ) , k'f(δ)
に訂正して読んでくれ。 >>371ミス訂正がさらに間違えとる。ダッシュを付ける場所がズレてるね。
まぁこのくらいならわかるだろうしえぇやろ。申し訳ない。 >>366
f'(x)=0 は三つの実数解を持ち、それらを小さい順に、s,t,u とすると、f(s)<0,f(t)>0,f(u)<0 である。
F(x)=f(x)+kf'(x) とすると、
F(-N)>0、F(s)<0、F(t)>0、F(u)<0、F(M)>0 (ただし、N,Mは十分大きな値)
なので、F(x)=0は4実数解を持つ ウォーキングで10kmの坂道を一定の速さを減速し続けながら登る。
時速6km/hで登り始め、時速4km/hで頂上に到着したものとする。
このとき、坂道を登るのに要した時間はいくらか?
これ教えてほしいです。
よろしくお願いします。
こんな明らかでないことが明らかに見えるなんて
数学が得意な人は怖いです
>>374
算数の問題かと思ったけど、物理の問題っぽいね
一定の速さで減速だから、加速度は一定、
すなわち、そのウォーキングは等加速度直線運動ということになる
物理の知識を使ったほうが簡単に解けそう
重力下での物体の投げ上げと思えばいいかも >>376
こういうのが悪い回答です
明らかにそういう趣旨ではないのに、自分の知識を元にして自分の解きたいように解くから、質問者の求めてるものとは違うものを出している >>376
時間ではなく進んだ距離に対して
一定の速度で減速する設定です >>374
これは高校数学じゃないような…
積分するまでもなく台形の面積の公式を使って
(6+4)*h/2 = 10
h = 2
かな? >>377
いや、あんまり書くと答えになっちゃうからさ
要は物理の問題なんだよ
時刻 t における位置を x(t) とするとき、速度 v(t) は位置の微分だから、
v(t) = dx/dt
で、一定の速度で減速だから、比例定数を a > 0 とすると、
v(t) = v(0) - at ( v(0) は初速度)
と書けるから、 v(0) と x(0) (初期位置)を問題のケースに合わせて設定すれば良い
これを単純に積分付きの連立方程式と思って解いてもいいけど、
高校物理の知識があれば等加速度直線運動だと思ったほうがわかりやすい
つまり、運動方程式
m dv/dt = F
において F = -ma とすれば問題に合致するから、これは重力下での物体の投げ上げと同一視できる ああ、ごめんちゃんと問題読めてなかったわ
>>374を「一定の速さで減速」と読み間違えていた
平面なら一定の速さで動くものと仮定して坂道によって減速するってことか >>378
つまり、時刻 t における位置(進んだ距離)を x(t) として、
そのときの速度を v(t) とすると、比例定数を a > 0 として
v(t) = v(0) - ax(t)
と書けるってことかな? そんなわけないですよね
>>379で正解でしょう
質問者が問題ちゃんと理解してるとは限りませんよ >>385
もしかして流水算と同じように考えてる?
問題文は
「ウォーキングで10kmの坂道を一定の速さを減速し続けながら登る。」
だから、そんなに単純じゃないと思うぞ
登れば登るほど登る速さが遅くなるってことでしょ? >>374
6^2-4^2=2*10*a
a=1.4
(6-4)/1.4=1.4285714 >>386
ボールを上に向かって投げるだけ、物理の力学で最初にならうよ。 v(t)=6-x(t)/5
dx/dt=6-x/5
dx/(6-x/5)=dt
-5log|6-x/5|=t+C
|6-x/5|=e^{-(t+c)/5}
6-x/5=±e^{-(t+c)/5}
x=30±5e^(-c/5)e^(-t/5)
C=±5e^(-c/5)とおく
x=30+Ce^(-t/5)
t=0のときx=0より
0=30+C
C=-30
よって
x=30{1-e^(-t/5)}
x=10のとき
10=30{1-e^(-t/5)}
e^(-t/5)=2/3
-t/5=log(2/3)
t=-5log(2/3)
≒2.02732554時間
≒2時間01分38秒
>>390
1ヶ所修正
v(t)=6-x(t)/5
dx/dt=6-x/5
dx/(6-x/5)=dt
-5log|6-x/5|=t+c←(小文字のcに修正)
|6-x/5|=e^{-(t+c)/5}
6-x/5=±e^{-(t+c)/5}
x=30±5e^(-c/5)e^(-t/5)
C=±5e^(-c/5)とおく
x=30+Ce^(-t/5)
t=0のときx=0より
0=30+C
C=-30
よって
x=30{1-e^(-t/5)}
x=10のとき
10=30{1-e^(-t/5)}
e^(-t/5)=2/3
-t/5=log(2/3)
t=-5log(2/3)
≒2.02732554時間
≒2時間01分38秒 v=e^(at)
6=e^(a*t0)
4=e^(a^t1)
∫[t0,t1]vdt=10
から
t1-t0を求める問題?
>>391
ちなみに
v=dx/dt
=6e^(-t/5) >>392
v=ds/dt=as
s=e^(at)
だな >>392
v(t)=ds(t)/dt=as(t)
s(t)=C*e^(at)
v(t)=aC*e^(at)
で
v(0)=6
v(t1)=4
s(t1)=10
のときt1を求める >>367
微分もプログラムに頼って
> D(expression((x-p)*(x-q)*(x-r)*(x-s)),'x')
(((x - q) + (x - p)) * (x - r) + (x - p) * (x - q)) * (x - s) +
(x - p) * (x - q) * (x - r)
しかし、
d/dx((x - p) (x - q) (x - r) (x - s)) = (x - p) (x - q) (x - r) + (x - p) (x - q) (x - s) + (x - p) (x - r) (x - s) + (x - q) (x - r) (x - s)
でWolframの出した式の方が綺麗。 wolframがタイムアウトするような計算は自分でできるはずもないからプログラム組んで数値解で計算。
受験板でもないからこれが効率的。
>>376-397さん
ありがとうございます
私の手に余る難問だと言う事だけは
完璧に理解できましたw >>395
v(t)=ds(t)/dt=as(t)+v0, (a<0,v0=6)
s(t)= Ce^(at) - v0/a
v(t)=aC*e^(at)
t0=0
v(t0)=aC=6
v(t1)=aCe^(at1)=4
s(t1)=Ce^(at1)-6/a=10
e^(at1)=4/6
C=6/a
(6/a)(4/6)-6/a=10
a=-1/5
6*e^((-1/5)t1)=4
t = log(243/32) = 2.0273255 >>374>>395
v(t)=ds(t)/dt=as(t)+v0, (a<0,v0=6)
s(t)= Ce^(at) - v0/a
v(t)=aC*e^(at)
t0=0
v(t0)=aC=6
v(t1)=aCe^(at1)=4
s(t1)=Ce^(at1)-6/a=10
e^(at1)=4/6
C=6/a
(6/a)(4/6)-6/a=10
a=-1/5
6*e^((-1/5)t1)=4
t1 = log(243/32) = 2.0273255 >>400
>391の値と一致しているから、正解だろうな。 >>373
>f'(x)=0 は三つの実数解を持ち
って自明じゃない気がする。
俺は説明なしではわからない。 すごい横だけど、運動生理学的には
歩いた時間に比例して一定の速度を減速するより
歩いた距離に比例して一定の速度を減速する方が
現実に即したモデルになってるの?
>>403
興味がでたので、プログラムを組んでグラフにしてみた。
道具の使えないガイジは手計算して手書きしてください。
> # 距離を与えて所要時間を返す

> t(10)
[1] 2.027326
> t(20)
[1] 4.054651
> # 時間を与えて走行距離を返す

> s <- function(t1,s1=10,v0=6,v1=4){
> s(1)
[1] 5.438077
> s(2.027326)
[1] 10
> s(5)
[1] 18.96362 >>402
y = f(x) はx軸と異なる4点で交わるから3つの異なるxの値で極値を持つのは自明だろ >>405
バグあったので修正
# 距離を与えて所要時間を返す

> t(10)
[1] 2.027326
> t(20)
[1] 5.493061
> t(25)
[1] 8.958797
> # 時間を与えて走行距離を返す
 >>405
>>405
> s(1)
[1] 5.438077
> s(2.027326)
[1] 10
> s(24)
[1] 29.75311 >>405
> 道具の使えないガイジは手計算して手書きしてください。
こういう煽りをするからプログラムキチガイと言われる事に気付け屑 グラフのタイトルもなければ単位も書いてない
やるならやるできっちりやれよと
>>374
これ面白いな。
この人が24時間坂道を上ったときにどれだけ歩けるか?とか
この人の走行可能距離はいくらか?とか
面白い問題が作れそう。
数値変えても計算できるように、俺はプログラムを組んだけど。 高校数学ではプログラムで問題を解決する方法は習わないんだから
このスレでは参考程度だよ
しかもグラフとしても不完全で分かりにくい
>>374はプログラムキチガイの自演だったんじゃないのか?
最終的にプログラムネタに持ち込むための 出発時の速度a(km/h)、到着時の速度b(km/h)
歩行距離X(km)、所要時間T(h)、としたとき
これらの関係はT=X(lnb-lna)/(b-a)
だからa=6,b=4,X=10のとき所要時間は
T=10(ln4-ln6)/(4-6)=5ln(1.5)=2.027…(h)
>>413
二次方程式の解の公式も簡単なプログラムだがw >>374
結局>>384の解釈で良いの?
それなら v(t) の式の両辺を t で微分すれば、 v(t) は微分方程式
v'(t) = -av(t)
を満たすから、これの解は C をある定数として
v(t) = Ce^(-at)
になる。
なので>>374の答えは v(t) = 4 km/h を t について解けば良い。
問題の条件から a と C の値が決まるから、答えだけ書くと
5log(3/2) 時間ということになる。
2時間とちょっとかかったことになるね >>416
>>72みたいなクソ問題は誰1人として興味を示していないじゃないかw
イナにすら相手にされていないw
構ってちゃんのキチガイレス乞食ジジイ >>418
ちなみに、 v(t) の微分方程式の両辺に物体の質量 m を掛ければ
m dv/dt = -amv(t)
になるから、これは運動方程式 m dv/dt = F において F = -amv(t) としたものになる
若干無理矢理だが
「質量と速度の積(=運動量)に比例する抵抗力を受ける物体の運動」と解釈することができる
やっぱり物理の問題って感じがする >408
>気付け屑
>気付け屑
>気付け屑
>気付け屑
>>419
数を減らした問題で別スレでは正解が返ってきたよ。
計算は面倒だから道具を使っていたけど。
あんたにゃ、無理そう。 >>415
プログラムはスレ違いだから敢えてやろうという気はない >>422
屑の負け惜しみw
別スレに貼った問題をわざわざ改題してこのスレに貼るレス乞食
別スレで出題したのも答えのもお前だろw自演野郎w >>404
>>373 のどこが間違い?
kに対する条件設定なんて、どこにも無いんだけど?
どっか、壮大に勘違いしてない? >>418
ところで、微分方程式 v'(t) = -av(t) は一応高校数学レベルでも解けることを示しておこう
要するに v(t) は微分すると元の関数の定数倍になるということだから、
なんとなく指数関数になりそうな気がするという直観に基づいて、以下のような計算のトリックを使う
移行して = 0 の形にして、両辺に e^(at) をかけると、
e^(at)v'(t) + ae^(at)v(t) = 0
となるが、実はこの左辺は (e^(at)v(t))' に等しい。
したがって両辺を t について積分すれば、積分定数を C として
e^(at)v(t) = C
が成り立つ。
ゆえに、
v(t) = Ce^(-at)
となる。 >>402
f(x)=0 が相異なる実数解をもてば、それらの間に f(x)の極値点がある。
(ロルの定理)
>>373
中間値の定理
>>366
微分のことは微分ですると・・・・
k=0のときは明らか。
k≠0 のとき
g(x) = k e^(x/k) f(x)
は f(x) =0 と同じ解をもち、さらに
k>0 のときは lim[x→-∞] g(x) = 0
k<0 のときは lim[x→+∞] g(x) = 0
(無限遠点も含めれば) 相異なる5つの実数解をもち、相異なる4つの極値点をもつ。
∴ g '(x) = e^(x/k)F(x) = 0 は相異なる4つの実数解をもつ。 >>423
グラフを書くのがプログラムかなぁ?
道具を使えないガイジは手計算して手書きすればいいよ。
定規を使うのもアウトかもね。
まあ、問題によっては折り紙を使った解法とかもあるけど、インチキとかカンニングとかいうんだろうな。 >>424
日本人におけるABO式血液型の割合は、おおよそA型40%、O型30%、B型20%、AB型10%といわれています。
この比率をちょうど、4:3:2:1として、全血液型を集めるのに必要な人数の期待値を求めよ
というまっとうな問題だよ。
できないのはガイジ。 >>431
レス乞食がまた負け惜しみを言ってる
誰にも相手にされない問題を出すプログラムキチガイ
そもそもここは高校数学の質問スレだ
日本語すら理解出来ないのか?
昨日のレスを見ろ
みんなお前に迷惑している
このスレの嫌われ者
存在価値0
オマエは実社会でもネットでも必要とされていない
キチガイはさっさと消えてしまえ >>430
一見して何を表しているのかもわからないものをグラフと言い張ったところで誰も相手にしないよ >>429
> f(x)=0 が相異なる実数解をもてば、それらの間に f(x)の極値点がある。
>(ロルの定理)
わかっているとは思うが、ロルの定理からわかるのは
a ≠ b かつ f(a) = f(b) ならば f'(c) = 0 となる点 c が a と b の間に少なくとも一つは存在する
ということだけで、その点 c が必ずしも極値点になるとは限らない
f(x) が2次以上の一変数多項式の場合はたまたま f'(c) = 0 となる c が有限個しか存在しないから
極値点になると言えるだけだよね? 実は期待値って高校数学の範囲外なんだよね
こないだ新入生に習ってないって聞いてびっくりした
>>429
>> (無限遠点も含めれば) 相異なる5つの実数解をもち
この五つ根のうち4つはf(x)由来、一つはe^(x/k)由来 という立場で主張しているのだと思うが、
その立場、つまり、無限遠の解も一つに数えるという立場に立つのなら、
>> ∴ g '(x) = e^(x/k)F(x) = 0 は相異なる4つの実数解をもつ。
こちらの四つの根のうち一つはe^(x/k)由来、三つはF(x)由来と考えることになり、
この問題の解答としては論理破綻してはいないか? >>431
簡単にいうが、最小公倍数とか、他の数値もあるわけで?
漠然としていないか?質問が、オカシイ
元の質問、みてないけど、これだと、普通に足したらいいんじゃないの?に
それが、比率をって説明するから、答えがそうなる
何故比率として、何対何対ってやりゃなければいけない
枠組みを設定したのか、疑問に思うが 最低限?それで
全てがそうなるのか? 正解が有って、現実的な確立と同じになるか? >>431
普通に計算せずに、100人でいいんじゃね?
それか、10人だw >>437
これ、質問者が理解出来ていないから、質問文が間違ってる事になる
これだから、誰も答えようとしない
指摘されても、理解が出来ていない わかっているとは思うが、f(x) は4次式だから
f(x) ≡ 0 (a≦x≦b)
などではない。 >>434
[a,b] において連続なる f(x) の最大値は正(最小値は負)である。
ロルの定理の証明もこれを利用しているんぢゃないか?
高木:「解析概論」改訂第三版、岩波書店 (1961)
§18. 定理19 p.47
>>436
0 < ε < (|g(x)|の極大値)
なるεに対して
0 < | g(-N) | < ε (k>0のとき)
0 < | g(M) | < ε (k<0のとき)
となる大きい数 M または N がある。そこで
g(x)-g(-N) あるいは g(x)-g(M)
に対してロルを適用する。 >>440
厳密にいえば、 f'(x) が停留点の前後で符号を変えることを確認する必要があるね
> f(x) ≡ 0 (a≦x≦b)
>などではない。
だけでは不十分
一般には f'(c) = 0 となる c のある近傍で常に f'(x) = 0 かもしれないから、
f'(x) が1次以上の多項式であることも使う必要がある
要するに代数学の基本定理が必要 >>440
つまり、>>429で、g(x) = k e^(x/k) f(x)=0 が5実数解を持つという立場の時は、
x→±∞ を含んでいるが、
>> ∴ g '(x) = e^(x/k)F(x) = 0 は相異なる4つの実数解をもつ。
の時は、g(x)を g(x)-g(-N) あるいは g(x)-g(M) と微少に変化させることにより、
x→±∞ という解を除いた上で、4実数解を持つ と結論できるという展開でしょうか。
それなら、論理的にはokですが、同時に>>429では解答として足りないと言うことになりますね。 >>72 クーポンコレクター問題(コンプリートガチャ問題)
>>431 4つの血液型の人を集める問題
( 他スレでの出題は2018年6月
http://2chb.net/r/math/1512229947/665 )
まともに場合分けして解くと、項数が n! のオーダーで爆発してしまうが
大学数学のラプラス変換などを使ってまとめると (2^n)-1 項の短い式にできる
公式の完全版は以下から
http://doryokujin.hatenablog.jp/entry/2012/05/09/034209
集めたいものが出る確率の比が a:b:c:d:... のとき
全部集めるための個数の期待値は
(a+b+c+d+...)×{
(1/a)+(1/b)+(1/c)+(1/d)+...
-(1/(a+b))-(1/(a+c))-(1/(a+d))-...
+(1/(a+b+c))+(1/(a+b+d))+...
-(1/(a+b+c+d))-...
+...
}
より簡単に、a=b=c=d=...=1のときは
高校数学でも簡単に解けて、n種類のとき
個数の期待値 E(n)=n×(1+(1/2)+(1/3)+...+(1/n)) >>441
> 厳密にいえば、 f'(x) が停留点の前後で符号を変えることを確認する必要があるね
f(x) ≡ 0 ではないから、
[a,b] において連続なるf(x) に正の最大値(または負の最小値)が存在する。
このとき f '(x) がその前後で符号を変えることは明らか。
> 要するに代数学の基本定理が必要
それだと 実数解と虚数解の区別がつかないのでは?
>>442
そのとおりですね。 皆様は予備校や塾で高校生に数学を教えているのですか?
>>445
>f(x) ≡ 0 ではないから、
>[a,b] において連続なるf(x) に正の最大値(または負の最小値)が存在する。
>このとき f '(x) がその前後で符号を変えることは明らか。
それは明らかではありません
それを明らかだというのは「グラフより明らか」というのと同じことです
なぜなら、最大値のある近傍で一定である可能性が排除できないからです
>一般には f'(c) = 0 となる c のある近傍で常に f'(x) = 0 かもしれない
これが起きないことを保証するために
>f'(x) が1次以上の多項式であること
が必要
>> 要するに代数学の基本定理が必要
>それだと 実数解と虚数解の区別がつかないのでは?
良いツッコミですが、そのようなツッコミが入ることは少々残念です
それらが全て実数解になることは 4 次多項式 f(x) が相異なる 4 個の実数根を持つことから、
f'(x) がちょうど 3 つの異なる実数根を持つことがわかるでしょう
つまり、 f(x) の 4 つの相異なる実数根を p < q < r < s とするとき、
f'(x) は 3 次多項式なので高々 3 つの根を持つが、ロルの定理より、
f'(x) の実数根 c[1], c[2], c[3] が p < c[1] < q < c[2] < r < c[3] < s を満たすように存在し、
したがってそれらが f'(x) の根の全てであることがわかります >>443
6個だと
1/a+1/b+1/c+1/d+1/e+1/f-
(1/(a+b)+1/(a+c)+1/(a+d)+1/(a+e)+1/(a+f)+1/(b+c)+1/(b+d)+1/(b+e)+1/(b+f)+1/(c+d)+1/(c+e)+1/(c+f)+1/(d+e)+1/(d+f)+1/(e+f))+
(1/(a+b+c)+1/(a+b+d)+1/(a+b+e)+1/(a+b+f)+1/(a+c+d)+1/(a+c+e)+1/(a+c+f)+1/(a+d+e)+1/(a+d+f)+1/(a+e+f)+1/(b+c+d)+1/(b+c+e)+1/(b+c+f)+1/(b+d+e)+1/(b+d+f)+1/(b+e+f)+1/(c+d+e)+1/(c+d+f)+1/(c+e+f)+1/(d+e+f))-
(1/(a+b+c+d)+1/(a+b+c+e)+1/(a+b+c+f)+1/(a+b+d+e)+1/(a+b+d+f)+1/(a+b+e+f)+1/(a+c+d+e)+1/(a+c+d+f)+1/(a+c+e+f)+1/(a+d+e+f)+1/(b+c+d+e)+1/(b+c+d+f)+1/(b+c+e+f)+1/(b+d+e+f)+1/(c+d+e+f))+
(1/(a+b+c+d+e)+1/(a+b+c+d+f)+1/(a+b+c+e+f)+1/(a+b+d+e+f)+1/(a+c+d+e+f)+1/(b+c+d+e+f))-
1/(a+b+c+d+e+f) 7個だと
1/a+1/b+1/c+1/d+1/e+1/f+1/g - {1/(a+b)+1/(a+c)+1/(a+d)+1/(a+e)+1/(a+f)+1/(a+g)+1/(b+c)+1/(b+d)+1/(b+e)+1/(b+f)+1/(b+g)+1/(c+d)+1/(c+e)+1/(c+f)+1/(c+g)+1/(d+e)+1/(d+f)+1/(d+g)+1/(e+f)+1/(e+g)+1/(f+g)} + {1/(a+b+c)+1/(a+b+d)+1/(a+b+e)+1/(a+b+f)+1/(a+b+g)+1/(a+c+d)+1/(a+c+e)+1/(a+c+f)+1/(a+c+g)+1/(a+d+e)+1/(a+d+f)+1/(a+d+g)+1/(a+e+f)+1/(a+e+g)+1/(a+f+g)+1/(b+c+d)+1/(b+c+e)+1/(b+c+f)+1/(b+c+g)+1/(b+d+e)+1/(b+d+f)+1/(b+d+g)+1/(b+e+f)+1/(b+e+g)+1/(b+f+g)+1/(c+d+e)+1/(c+d+f)+1/(c+d+g)+1/(c+e+f)+1/(c+e+g)+1/(c+f+g)+1/(d+e+f)+1/(d+e+g)+1/(d+f+g)+1/(e+f+g)} - {1/(a+b+c+d)+1/(a+b+c+e)+1/(a+b+c+f)+1/(a+b+c+g)+1/(a+b+d+e)+1/(a+b+d+f)+1/(a+b+d+g)+1/(a+b+e+f)+1/(a+b+e+g)+1/(a+b+f+g)+1/(a+c+d+e)+1/(a+c+d+f)+1/(a+c+d+g)+1/(a+c+e+f)+1/(a+c+e+g)+1/(a+c+f+g)+1/(a+d+e+f)+1/(a+d+e+g)+1/(a+d+f+g)+1/(a+e+f+g)+1/(b+c+d+e)+1/(b+c+d+f)+1/(b+c+d+g)+1/(b+c+e+f)+1/(b+c+e+g)+1/(b+c+f+g)+1/(b+d+e+f)+1/(b+d+e+g)+1/(b+d+f+g)+1/(b+e+f+g)+1/(c+d+e+f)+1/(c+d+e+g)+1/(c+d+f+g)+1/(c+e+f+g)+1/(d+e+f+g)} + {1/(a+b+c+d+e)+1/(a+b+c+d+f)+1/(a+b+c+d+g)+1/(a+b+c+e+f)+1/(a+b+c+e+g)+1/(a+b+c+f+g)+1/(a+b+d+e+f)+1/(a+b+d+e+g)+1/(a+b+d+f+g)+1/(a+b+e+f+g)+1/(a+c+d+e+f)+1/(a+c+d+e+g)+1/(a+c+d+f+g)+1/(a+c+e+f+g)+1/(a+d+e+f+g)+1/(b+c+d+e+f)+1/(b+c+d+e+g)+1/(b+c+d+f+g)+1/(b+c+e+f+g)+1/(b+d+e+f+g)+1/(c+d+e+f+g)} - {1/(a+b+c+d+e+f)+1/(a+b+c+d+e+g)+1/(a+b+c+d+f+g)+1/(a+b+c+e+f+g)+1/(a+b+d+e+f+g)+1/(a+c+d+e+f+g)+1/(b+c+d+e+f+g)} + 1/(a+b+c+d+e+f+g)
道具の使えないガイジには8個の場合の式はかけないだろうな。
>>ZvNkoL1/
そんなことより
期待値 =
4
+ 4人集めて達成しない確率
+ 5人集めて達成しない確率
+ 6人集めて達成しない確率
+ 7人集めて達成しない確率
+ 8人集めて達成しない確率
+ 9人集めて達成しない確率
つづく
これを証明してみろよ。出題者なら出来るだろう。
制限時間はIDが保持できる間
またプログラムキチガイが登場かよ
ただ式が面倒になるだけで何の面白味のない問題でマウントが取れると思っているのが笑える
>>453
彼は彼なりに楽しんでいるようだから放っておけばいい
数学の楽しみ方は人それぞれ お前の子供にも同じ事をされてもいいって事だな
高校数学の問題でヘルプ頼まれても因果応報マウントされてもお前は文句を言えない
三角関数の倍角公式だって一種のプログラムだよなぁ。
二次方程式の解の公式もそうだし、極端な話九九だって公式みたいなもんだな。
簡単に因数分解できる2次方程式すらPCに頼らないと解を出せないプログラムキチガイ
>>457
式変形もPCが出せるものはPCに頼る。
それができないのはプログラムを組んで数値解を出す。 >>448
もしも f(x) が正なる値を取るならば、[a,b] において連続なる f(x)の最大値は正である。
その最大値を f(ξ) とする(定理13)。然らば f(ξ) >0 だから a<ξ<b.
f(x)=f(ξ) となるxは高々有限個だから、それらを含まない小区間を取れば(*)、
f(x) - f(ξ) < 0. 故に
x-ξ > 0 とすれば {f(x)-f(ξ)}/(x-ξ) < 0 従って f '(y_1) ≦ 0,
x-ξ < 0 とすれば {f(x)-f(ξ)}/(x-ξ) > 0 従って f '(y_2) ≧ 0,
となる y_1 > ξ > y_2 がある。
(*)
> 一般には f '(c) = 0 となる c のある近傍で常に f '(x) = 0 かもしれないから、
f(x) が4次式の場合、それはありません。
後半はほとんど自明のような希ガス >>461
自明の定義は各人違うから証明問題には関わらんことにしている。
例外を探すプログラムを組むのは楽しいけど。
たいていメモリ制限で徒労に終わるw >>453
手書きで式を検証してくれ。
バグ指摘できればあんたらの好きなマウントがとれるぞw 黄チャートに出てきたんですが、これどうやって計算して右にもっていけばいいですか?
普通の二重になってる分数の外し方はわかるんですがこれが解けなくて……

あ、申し訳ないですタイポしました
問題集は1+a/bになっていて、私はそれでもわからないです
左辺の分母分子にbを掛ける
分子はa→ab
分母は(1+a/b)→b(1+a/b)=a+b
となる
>>467
早速ありがとうございます!!
質問したことがお恥ずかしいくらいめちゃくちゃ単純ですね
スッキリしました >>67
> 一辺の長さが1の正77角形の高さを手計算する?
> 普通、プログラム書いて数値計算するだろ。
> そうでないなら計算式を書いてみてくれ。
>>85
> 怒涛の計算力と根性があれば77角形の高さは計算できるぞ。
> 実際に答を書くこともできない池沼みたいだしね。
怒涛の計算力も根性もない人が手計算で出した答え
(1/sin(π/77)+1/tan(π/77))/2
プログラムキチガイがPCで出した答え
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
プログラムキチガイ「こんな式になってしまった。もっと簡単にできるかもしれん。」
道具に頼る事しか出来ないバカ >>469
数値あってるだろ?
手書きで検算したの? >>470
> 数値あってるだろ?
数値が合えばそれでいいと思ってる池沼キチガイ >>471
手書き計算で検算したの?
間違っていたらあんたの好きなマウントがとれるぞ。
計算過程を書いてみ!!
俺は計算器使うけど。 質問なんですが
1を2000として、7を50000とした時
2~6に入る数字を均等な間隔で求めるにはどうすればいいでしょうか?
>>471
小銭で払おうが紙幣で払おうが支払い金額があっていればいいぞ。 >>473
(50000-2000)÷6=8000ずつ刻めばいい
1 2000
2 10000
3 18000
4 26000
5 34000
6 42000
7 50000 >>472
何でお前のバカな解答を検算する必要あるんだ?
数1の単純な問題なのにマヌケな答えしか出せなかったカス
お前の数学のレベルが知れるわ >>474
的外れなレス
もし試験でその問題を出されてもPCがないと解答出来ない池沼
仮にその式を解答として書いたら減点されるのは必至 何度もすみません
左の場合、>>475さんの答えで確かに正しいんですが
右のように加速して7で50000になるようにするには
どう計算すればよいでしょうか?

>>478
受験スレじゃないから。
>4を熟読しろよ。 >>480
やはり池沼だな
ここは高校数学のスレなんだけど
分数は約分する
ルートは簡単な形に変形する
同類項は纏める
といった具合に出来るだけ簡潔な形で表現するのが基本だという事さえ分からないキチガイ
それにここは「質問」スレなんだが
「出題」スレではない
スレタイを100万回読んでから出直せ 小銭で払おうが紙幣で払おうが支払い金額があっていればいい。
>もし試験でその問題を出されてもPCがないと解答出来ない池沼
勝手に試験スレにしているガイジ
>>479
加速と言っても色々ある
x^2とかx^3とかa^x(指数関数的)とか
しかもこれらのグラフのどの部分をフィットさせるかでも答えは変わってくる >>483
小銭は同一硬貨が20枚を超えると受け取り拒否出来るのを知らないバカ
お前のレスは受け取り拒否
この板からも拒否
早く出て行けよ
キチガイの嫌われ者w >>484
「もし」と書いているのが読めない文盲
仮定って意味分かる?
中卒の爺には難しいかな? 要するに、このスレはシンメトリック解で答える事を要請されてるんだよね
何で近似解オナニー見せつけてるの?
>>485
レスありがとうございます!
出直してきます! >>487
もし道具が使えないガイジがいたら臍を噛んで死ぬのが正しい。 >>486
1000円を500円玉二枚で払えるぞ。 >>461
もしかして指摘の意味が分かってない?
>(*)
>> 一般には f '(c) = 0 となる c のある近傍で常に f '(x) = 0 かもしれないから、
>f(x) が4次式の場合、それはありません。
まさにそこが重要なポイントだということを指摘しているんだよ
「 f(x) が4次式だから」ではなくて、むしろ「 f'(x) が3次式だから」ということが重要
自明だと思えるのは代数学の基本定理を知っているからでしょ?
上の議論については、その議論では f'(x) が x = ξ の近傍で符号を変えることは言えていない
f'(x) = 0 ではダメなのだから ≦ 0 や ≧ 0 では意味がないし、
そもそも存在を示しても意味がない
証明すべきことは、 ξ のある近傍に属する全ての x について
「 x > ξ ならば f'(x) < 0 」かつ「 x < ξ ならば f'(x) > 0 」
でしょ? >>461
ちなみに f'(x) が連続であることを使えば、より一般に次のような命題が考えられる
【命題】 f(x) を実数全体で定義された(多項式とは限らない)実数値関数とする。
f(x) がいたるところ微分可能かつ導関数 f'(x) がいたるところ連続で、かつ
f(x) = 0 の解が有限個で、それらの全てを a[1] < a[2] < … < a[n] (n > 1) とし、
f'(x) = 0 の解が高々 n-1 個であると仮定する。
このとき、 f'(c) = 0 ならば、点 c は f(x) の極値点である。
(命題の証明) f(a[1]) = f(a[2]) = … = f(a[n]) = 0 であるので、ロルの定理より、
f'(b[k]) = 0 かつ a[k] < b[k] < a[k+1] (k = 1, 2, … , n-1)
となるような b[k] が存在する。
仮定より f'(x) = 0 の解はこれら b[k] で全てであるので、
f'(x) は開区間 (-∞, b[1]), (b[1], b[2]), … , (b[n-2], b[n-1]), (b[n-1], ∞) において常に正または負である。
(もしそうでなければ、 f'(x) の連続性に矛盾する。
実際、もし f'(x) が符号を変えるなら中間値の定理によってその間に零点を持つことなるが、
f'(x) の零点は b[k] のみであるのでこれは不可能である。)
さて、 (-∞, b[1]) において常に f'(x) > 0 と仮定すると、 (b[1], b[2]) においては常に f'(x) < 0 である。
なぜなら、このとき f(x) は (-∞, b[1]) において単調増加であるので
f(a[1]) = f(a[2]) = 0 かつ a[1] < b[1] < a[2] より f(b[1]) > 0 であるが、
もしも (b[1], b[2]) において常に f'(x) > 0 ならば f(a[2]) > 0 となるので矛盾する。
ゆえに b[1] は f(x) の極値点である。
同様に、 b[2], … , b[n-1] も f(x) の極値点であることがわかる。
(-∞, b[1]) において常に f'(x) < 0 の場合も同様である。 >>491
まだプログラムキチガイがいた
お前の解答は、千円支払うのに一円玉を千枚出すようなマヌケな解答
すぐに一円玉が千枚あるのか確認出来ない
それすら分からない知恵遅れは死ぬ >>495
道具が使えないないとパチンコ玉を手で数えんの?
紙幣も今は機械でカウントするぞ。 >>497
如何にも知恵遅れらしい発言wwwww
コイツは紙幣1枚すら機械で数えるらしいwww
発達障害ってやつ?ある1つの事に対して異常なまでに執着する
何が何でも機械でやらないと発狂する脳を持ってるんだなwww >>443
あの~、概念が間違っている
そもそも、100人に対しての統計でパーセンテージが振り分けられている
それを、何故 料理での割合等で用いられる
何対何、しょうゆ、ソース、マヨネーズをそれぞれ1対1対1で
人数分で、それぞれ倍にして下さい、みたいなのに
転換されて出題されなきゃならんのだ?
100人居て、40人がA型ならば、100×4タイプで
400人居れば良いし、なんならハッキリとA型の人とか
他の血液型が判別出来ている人でも集めれば良いだろう?
何この質問? 何企んでいるんだ? 学術の巨大掲示板群 - アルファ・ラボ http://x0000.net
数学 物理学 化学 生物学 天文学 地理地学
IT 電子 工学 言語学 国語 方言 など 多分、血液型の質問、屑のクイズ質問として、回答するならば
「全部の血液」を集めるのに「必要な人数」は、 4人ってなるんじゃないの?
質問者が多分、サイコパス
サイコパス診断の質問とか、犯罪の動機を聞いて初めて診断としての設問になるんだが
狂気じみてて変w
集合A={x∈N | 2≦x≦4}
このとき
ある条件xの条件が成り立つすべての要素xの集まりが集合A
となるので
集合A={2, 3, 4}
要素x=2,3,4
従って、
すべての要素xに対して集合pを満たす
のような言い回しは成り立ちますでしょうか?
訂正
>すべての要素xに対して集合pを満たす
すべての要素xに対して集合Aを満たす
意味不明で成り立たないとの事ですので、
正しく理解するために質問を細かく分解して聞き直させて下さい
集合A={x∈N | 2≦x≦4}
このとき
1)
ある条件xの条件が成り立つすべての要素xの集まりが集合A
となるのは成り立ちますか?
2)
集合A={2, 3, 4}
となるのは成り立つとして、
要素x∈{2,3,4}
となるのは成り立ちますか?
また、
要素x=2,3,4
となるのは成り立ちますか?
3)
すべての要素xに対して集合pを満たす
となるのは成り立ちますか?
またやってしまった、訂正
>すべての要素xに対して集合pを満たす
すべての要素xに対して集合Aを満たす
ごめんなさい、文章直しました
意味不明で成り立たないとの事ですので、
正しく理解するために質問を細かく分解して聞き直させて下さい
集合A={x∈N | 2≦x≦4}
このとき
1)
"ある要素xの条件"が成り立つすべての要素xの集まりが集合A
となるのは成り立ちますか?
2)
集合A={2, 3, 4}
となるのは成り立つとして、
要素x∈{2,3,4}
となるのは成り立ちますか?
また、
要素x=2,3,4
となるのは成り立ちますか?
3)
すべての要素xに対して集合Aを満たす
となるのは成り立ちますか?
集合と命題に対する根本的な理解が足りていないと思われ
数学Aの教科書を読みましょう
ここまで用語がめちゃくちゃだともうなんかアレだな……
こいつのいう「成り立つ」や「となる」「満たす」などが
一般の用語と乖離した意味・用法で都合よく多義に使われてるのとかは
何と言うか 1/0が undefined なことを「解なし」って言ってしまうアレに似てる
蓋し「解なし」病とでも呼ぶべき症状だ
>>499
因みに、お好み焼きのソースでは
ソース1:マヨネーズ1:ケチャップ1
で、美味しいw
>>501
サイコバス診断って、犯罪者に対して犯行の動機を聞いて
理解に苦しむ答えっていうのが有る。
一定の犯罪者の部類には、共通する狂気染みた回答をするんだとか
初めに犯罪も何もないのに、質問があるならば、質問者が異常者何だと思う >>431
AB型が10%の確率が確定的、断定が出来るのであれば、
100÷10=10で、10人必要?
でも、比率を対としてするなら、1・・・
おめー4って、A型が4人も必要だとかか?
つーか、質問文がまともじゃないじゃんッ >>509
よーしがんばって答えちゃうぞー
(1)
>"ある要素xの条件"が成り立つすべての要素xの集まりが集合A
正しいです。
(2)
「要素x」が何を意味する表現なのかが明確でないので答えにくいです。
もし集合Aの要素を1つもってきてxとする。ということであれば、
「x∈{2,3,4}」は正しいです。「x=2またはx=3またはx=4」は正しいです。
「x=2,3,4」は「x=2またはx=3またはx=4」と解釈することが多いですが、前後の文脈によっては異なる意味に解されることもなくはないので
それ単独では正否を判断しにくいです。
(3)
>すべての要素xに対して集合Aを満たす
明確な誤りです。
「〇〇を満たす」という表記をする場合、〇〇の部分には“条件”が入るわけなので“集合A”は条件ではないから誤った表現です。 >>512
他に対で表現されるのは、
お好み焼きにおいて、小麦粉70gに対し30gなので
7対3の割合で、全体の粉の量が100gよりも多くするならば、
これによって、120gに全体量をあげた時のそれぞれの量が
算出される
120×70%=84g 120-84=46g
因みに私はキャベツは5ミリ幅と聞いて、凄く美味しかった!
小麦粉70gきな粉30gに卵1個 豚コマ30g 牛乳120cc キャベツ140g
がすきー >>515
ものすんげースレチだが
パンの耳をザクザクして90gに牛乳150cc卵1個を
混ぜ合わせてフライパンで焼くと フレンチトーストっぽいw
150ccの牛乳にパン粉では、最大値の粉の量なのか判別付かないが
卵1個で固まる最大値に出来上がっている筈だ
数学は便利w >>498
税務署で高額現金納税したことないの?
機械で2回数えていたぞ。 >>517
オッケー! きちんとした様な問題文を、読みました
私、商業高校で、期待値とかは習ってないんですよね・・・
全部でXの種類のカードが有り、このXを全種、揃えられるまでの回数を求めよ
これだけだと、他に与えられるべき条件が不足されている
先ずは、全体数が抜かされている X種類のカードに対し、それぞれ何枚が用意されているのか?
同じ種類が何枚用意されていて、それは他のも要るし、全体数を出してから、それから計算が始まるんだが
質問が漠然としていると、私には思える これだけだと、XかけるXの数だけのジジョウ ここだけの話、普通にはプレミアムが付く、貴重なくらいの、少ない種類もある
それぞれの種類の割合がわかれば、多分、プレミアムを引く割合が出せるが、
大体がお店側の気まぐれだもの・・・
Aのみ一枚で、他は三枚ずつ有る、全部で50種類のクーポンが有る 全種類引くまで、おおよそ何枚でしょう?
これだと、文章の読解力の無い人が、最後の数値の意味が取れないかもしれない 全部で何枚引くか
でないと、置き換えで説明していた人は特に、混乱しそうだ もしかしたら私も読み返したらイミフかもw
血液で変換すると、
A、B、AB、Оの、4種類の血液型の人が居ます
無作為に選びだし、全種類の血液型の人を選び出すのには、何人必要になりますか?
それぞれの比率は A40% B30% AB10% О20% とする
これ、さっきのと同じ文章なのね?
4種類×一番少ないばーんてーじのが必要で。。。
だから、4×10人で、40人が答えになるようだが・・・
100人で10人だから、10人では1人はいる ならば10人が正解の筈 何故はじめに誤解が生じているのか?
??? 何が起きた・・・? 質問がどこかで可笑しくて、答えが変なんだけどw
>>523
ABが10%って、既に割合が出ているwwww
ナニコレwwwww
比率とか、占める割合だのってwwww ナニwwww
質問文、やっぱ変だよ >>518
知恵遅れwwww
紙幣1枚を払うのが高額納税者とはwww
あくまでも機械にこだわる発達障害の知恵遅れwwww
手で数えればいい場面もあれば機械でカウントする場面もある
ただそれだけなのに
そんな単純な事すら理解出来ない知恵遅れwwww
計算も同じ
手計算で十分な場面もあればPCによる計算が必要な場面もある
ただそれだけ
臨機応変って事が分からない
これも典型的な発達障害の症状
哀れだなwww >>518
あれ?
お前、中学生って設定だったよな?
中学生が高額納税者www
自分の設定を忘れる知恵遅れwww ある国の大統領選に A, B の 2 人が立候補した.選挙予想をするために,有権者から無作為 に調査対象を選び出し,A, B どちらの候補者を支持するかアンケート調査をしたところ
無作為 に選んだ 300 人中 180 人が,A を支持すると回答した.
そのとき,以下の問いに答えよ
2-1. 標本比率(標本平均) x の値を以下の中から選択せよ
(1) 0.2, (2) 0.3, (3) 0.4, (4) 0.5, (5) 0.6
2-2. A の支持率 p の 97% 近似信頼区間を求めよ
(1) [0.5445628,0.6554372], (2) [0.5386231,0.6613769], (3) [0.5271397,0.6728603],
(4) [0.5010192,0.6989808], (5) [0.4916005,0.7083995]
1ばんめは0.6と分かります
2ばんめがわかりません
>>529
信頼区間が97%なら(2)が答え
(もし95%なら(1)が答え)
こんなに有効数字を多く取る意味はあるのか?
如何にもプログラムを使って計算しましたみたいな選択肢だな
これプログラムキチガイの投稿だろ?
「手計算でやるの?道具を使わないの?」
ってマウント取るために出題したと予想 >>514
(2)
ここの説明、すごくわかりやすかったです。
(3)
「○○を満たす」の用法が間違っている事に気づけました
丁寧に答えてくれてありがとう御座います 数学的帰納法について質問です
x1+x2+……xn=0が成り立つ時、
|cosx1|+|cosx2|+……+|cosxn|≧1(間違っていると思います)を証明する
(ⅰ)
x=1のとき
x1=0より成り立つ
(ⅱ)
n=k(k≧2)の時成り立つと仮定すると
|cosx1|+|cosx2|+……+|cosxk|≧1…A
n=k+1の時
|cosx1|+|cosx2|+……+|cosxk|+|cosx(k+1)|
≧1+ cosx(k+1)|(∵A)
≧1
よって成り立つ
(ⅰ)(ⅱ)より、すべての自然数について成り立つ
という証明を考えたのですが、実際はx=2の時に成り立たないと思います
(x1=90°、x2=-90°)
どこが間違っているのでしょうか?
よろしくお願いします
>>532
n=k+1のとき条件とするのは
x1+…+xk+x(k+1)=0でしょ
ここからx1+…+xk=0は言えないからn=kのが使えない >>533
なるほど!
納得しました
ありがとうございました >>529
信頼区間は計算方法を指定しないと駄目だね。
これくらいあるから、ご要望に応じて有効数字を増やしてみましたw
> binom.ci(180,300,cl=0.97)
method x n mean lower upper
1 agresti-coull 180 300 0.59999999999999998 0.53751232549221739 0.65939666785540307
2 asymptotic 180 300 0.59999999999999998 0.53862057512889128 0.66137942487110868
3 bayes 180 300 0.59966777408637872 0.53820349502775999 0.66037857748282425
4 cloglog 180 300 0.59999999999999998 0.53575012384118081 0.65828387462549276
5 exact 180 300 0.59999999999999998 0.53606527893908784 0.66154967538056475
6 logit 180 300 0.59999999999999998 0.53735961649560871 0.65953275468399286
7 probit 180 300 0.59999999999999998 0.53763369511946668 0.65991097431682899
8 profile 180 300 0.59999999999999998 0.53781454269756002 0.66010191241316285
9 lrt 180 300 0.59999999999999998 0.53783138809278919 0.66013182252111757
10 prop.test 180 300 0.59999999999999998 0.54195356905609038 0.65544231701874112
11 wilson 180 300 0.59999999999999998 0.53753162278077349 0.65937737056684687 道具が使えないガイジってこういう問題をどうやってとくの?
円錐の展開図の渦巻を書いて円錐にしたときの作図をせよ。

>>535
プログラム組んでグラフにすると違いがわかるね。

>>528
子供が中学生。
俺が中学生と書いたソースあれば出してみ。
日本語もまともに読めないガイジがおまえだよw >>540
誰が中学生だとも書いてないじゃん。
やっぱりアホだ。
子供が中学生かもしれないし、兄弟が中学生かもしれんぞ。 >>542
キチガイのアスペ
519:132人目の素数さん 2020/07/12(日) 09:47:31.70 ID:lCCkuzVr
>>518
もしかして結構なお年?
521:132人目の素数さん 2020/07/12(日) 09:51:09.98 ID:PLqlj++l
>>519
中学生だけど
このやり取りを見て子供の年齢を答えたと解釈するのかよ
キチガイ丸出しの知恵遅れは死ね >>543
可能性を想定できないあんたがアホなだけ。 >>523
乱数発生させてシミュレーションすれば
理論値と一致していて楽しいぞ。 >>544
中学生である設定を忘れた事を誤魔化すのに必死だな
キチガイのクズは死ね フィーリングカップル5対5とかも
理論値とシミュレーションが一致して楽しめる。
>>546
明らかにスレ違いだな
知恵遅れは消えてしまえ >>523
a=1/10,b=2/10,c=3/10,d=4/10と置いて理論値は
1/a+1/b+1/c+1/d - (1/(a+b)+1/(a+c)+1/(a+d)+1/(b+c)+1/(b+d)+1/(c+d)) + (1/(a+b+c)+1/(a+b+d)+1/(a+c+d)+1/(b+c+d)) - 1/(a+b+c+d)
簡単なプログラムを組んでシミュレーションすると
sim <- function(p){
n=length(p) # number of items
if(sum(p)>=1){ # no blank and/or rate of probabilities
prob=p/sum(p) # scaling for sum(prob)=1
lot=1:n # no blank lot
}else{
prob=c(p,1-sum(p)) # blank with probability of 1-sum(p)
lot=1:(n+1) # lot[n+1] blank lot
}
y=NULL
while(!all(1:n %in% y)){ # unless all item got
y=append(y,sample(lot,1,prob=prob)) # sample one lot with probabilty prob
}
return(length(y))
}
これを1000万回やって平均値をだすと
> mean(replicate(1e6,sim(1:4/10)))
[1] 12.35857
理論値に近似している。 >>548
・男女がn人ずついる
・各男性はランダムに女性を一人選ぶ
・各女性はランダムに男性を一人選ぶ
・お互いに選び合った男女でカップルが成立
男女100人ずついるとして、5組のカップルが誕生する確率は? >>545
それを消防署から来たという主張だと考える椰子は知恵遅れといえる。 逆に中学生の子供がいる身分で平日の昼から数学板に書き込みしてる方がやべーよ
なんかこのスレ荒らしも嵐を煽ってる側も他のスレと比べて子供っぽいんだよな
この板の住人ではないお客様ばかりというか
荒らしでない側も論理的な指摘より煽りあいで喜ぶようなお客様だし他板に移転したらいいのでは?
このスレにいる人は他のスレについていけない人が大半であろつ
お客様が素直に他の板に移ってくれるというのは安易な考えで、
他のスレにちょっかいをかけにいかないようこのスレに集めておくというのが隔離スレの発想だろう。
まぁ夏に生ゴミが発生するのはしゃーない。
ドヤ顔して高校数学の範囲外すんななど言ってるような人たちは自分がこの板にとってのお客様だとは思いもよらないだろうから、隔離スレは必要
この数学的に無価値なスレで荒らし同士なんの正当性もない煽りあいをし続けてくれてそれでオーケー
>>558
それもこのスレの話題としては適切かなと理解しました >>547
中学生にマウントとられていることになんの?
>551を手計算でできたら立場逆転のチャンスだぞw ある程度5chやってきた人ならNGワード登録が最善だと分かってるでしょ
5chで自治することは難しいから
>>561
「w」でも消しきれませんが何をNGにしてますか? 死ね, キチガイ, ガイジ, 知恵遅れ など罵り言葉を全部
>>560
誰もお前が中学生とは思ってないんだがwww
自称中学生のキチガイって事はみんな知ってるしな
しかも数学Iの三角比の問題でさえパソコンを使わないと解けないザコwww
お前中卒だろwww
中卒コンプレックスがあるからスレ違いの問題を出してマウント取ろうとしてる知恵遅れの猿www 小学生が筆算を習っているところへ電卓持ってきて見せびらかしているようで
痛さが半端ないというか
各面が合同な多角形でできた凸な多面体は、私が知ってるのは
5種類の正多面体 と
合同な2つの正四面体を1つの面で接合してできる6面体
なのですが、ほかにありますか?
>>566
正多角形でなくてもいいならいくらでもあるんじゃ? こういうのか


>>556
高校数学くらい真面目にやってもバチは当たらんだろ
手の内を明かしたくないからって数学的に価値のある議論なんてどうせできないんだから >>566
ちなみに各面が正多角形であるであるようなものもいくらでもある。
簡単なところだと、側面がすべて合同な正三角形で底面が正五角形でようなある5角錐を2つ底面で接合してできる10面体など。 いくらでもは言い過ぎか。数は少ないね。
各面が正多角形の場合は、正三角形の場合に限り1つの頂点に集まる面の数が3~5個ありえるので
頂点ごとに集まる面の数を変えれば各面が合同な正三角形ではあるが正多角形でないものが作れる。
>>570でくっつけている2つの5角錐の間に
正三角形10個を互い違いにくっつけてぐるりと輪にしたものを1つ挟み込んだ図形のことを正20面体というけれども
この挟み込む輪の数を増やしていけば何個でもすべての面が合同な正三角形である凸多面体が作れるね。 その5角錐を正12面体の各面に貼るとそれも凸にはならないっぽい
wikiでデルタ多面体という言葉を見つけた
結局、正多面体以外だと
正4面体を合わせたやつ
5角錐を合わせたやつ
3角柱の側面に4角錐を貼ったやつ
2つの4角錐の間を8つの正3角形の輪で埋めたやつ
2つの5角錐の間に2つの正3角形を挟んだやつ(←謎い)
しかない感じなのか
>>509
> ごめんなさい、文章直しました
>
> 意味不明で成り立たないとの事ですので、
> 正しく理解するために質問を細かく分解して聞き直させて下さい
>
> 集合A={x∈N | 2≦x≦4}
> このとき
>
> 1)
> "ある要素xの条件"が成り立つすべての要素xの集まりが集合A
> となるのは成り立ちますか?
整数についてのある条件(2以上であり4以下である)を満たすすべての整数の集合がA
と書くのが普通の書き方。
>
> 2)
> 集合A={2, 3, 4}
> となるのは成り立つとして、
> 要素x∈{2,3,4}
> となるのは成り立ちますか?
Aの要素xについてx∈{2,3,4}は正しいですか?
なら、その通り。
> また、
> 要素x=2,3,4
> となるのは成り立ちますか?
x∈Aなら x=2、またはx=3、またはx=4 である
と書くのがまぎれがなくよい。
>
> 3)
> すべての要素xに対して集合Aを満たす
> となるのは成り立ちますか?
言いたいことが
A={2、3、4}のとき {2、3、4} の任意の要素 x について x∈A ですか、
なら、正しい。。 >>509の質問に対して
>>514が返答をして
>>531でお礼を述べている。
~~ここまで普通のやり取り~~
>>577 突然40レス以上も前の解決済案件についての独自見解を述べる???
ここから長きにわたり無為な議論を始めたいんだという強い意志が感じられる。 表現が独特なのでそこを突き詰めることに興味が湧いたのだよ。
>>566
等面4面体がある。
各面が合同な鋭角⊿
鋭角⊿とその中点⊿を展開図とする。
4点 (a,b,c) (a,-b,-c) (-a,b,-c) (-a,-b,c) を頂点とする。
n方両錐
2つの正n角錐の底面を貼合せたもの。 母線の長さが1、円錐角(母線と軸のなす角)がθの円錐側面の展開図を頂点を原点にy軸に対称に置く。
尚、円錐底面の円の展開は考えない。
円錐側面展開図上の点Aの座標を(p,q)とすると展開図を円錐化したときのAの三次元座標をp,q,θで表わせ。
>>564
マウントをとりたがるのは猿だけ。
ボノボですらそんな行動はしないね。
>>584
Wolframは分数で出しちゃうね。 >>566
最近発表されたものだとこんなのもあるね
将棋の駒のような5角形を合わせた24面体
(四方六面体の変形)

>>443
クーポンコレクターにラプラス変換とか必要なん?
高校範囲でその公式出せるんちゃう? >>585
数Iレベルの三角比すら分からなかった猿以下の知能しか持たないアホが何か言ってるw 質問者です
>>577
>>578
意図した内容になるような正しい文章を提示してくれたと言う意味において
私的にはとても有益ですよ 次のデータを得た
7.5, 5.5, 4, 7, 8.5, 5, 9, 9.5
データは正規分布に従うとする.そのとき,以下の問いに答えよ
1. 標本平均 x の値を以下の中から選択せよ
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
2. (不偏)標本分散 s^2 の値を以下の中から選択せよ
1. 自由度 7 のティー分布の両側 0.1 点 t7 (0.1) の値を以下の中から選択せよ
(1) 1.8595, (2) 1.8946, (3) 2.3060, (4) 2.3646, (5) 3.4995
2. 母平均 µ の 90% 信頼区間をを以下の中から選択せよ
(1) [5.685135,8.314865], (2) [5.660315,8.339685], (3) [5.369412,8.630588],
(4) [5.327975,8.672025], (5) [4.52548,9.47452]
>>588
数値は違っていた? 手計算で検査してないの?
>>584
そのページの結果が正しいことはどうやって検証すんの?
俺は、
fcmf=function(m,f){
Boys=1:m
Girls=1:f
Selected.Boys=sample(Boys,f,replace=TRUE)
Selected.Girls=sample(Girls,m,replace=TRUE)
n=min(m,f)
hit=numeric(n)
for(i in 1:n){
j=Selected.Girls[i]
hit[i]=(Selected.Boys[j]==i)
}
return(sum(hit))
}
mean(replicate(1e7,fcmf(100,100))==5)
でできるけど。 >>582
展開図の座標軸の向きと立体の座標の入れ方は必要あるね。 >>591
> 数値は違っていた? 手計算で検査してないの?
数値さえ合えばいいと思っている池沼www
>>169
> 1辺の長さ1の正7角形の高さの厳密解を求めたら
> こんな式になってしまった。もっと簡単にできるかもしれん。
>
> (sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
この式を簡単に出来ないバカwww
ソフトを使わなければ簡単な式変形すら出来ない低脳のジジイwww
逆か!
簡単な計算すら出来ない知的障害者だからソフトに頼るのかwww このスレでは草を生やし数学的レスには高校範囲外を突きつけることが必勝法
>>593
こういうのは答が出せても作図できないと楽しくないね。 >>594
数値が合えばいいんじゃないの?
電卓も内部計算はテイラーてんかとかでやってんじゃないの? >>597
だから池沼って言われるんだよ
数Iレベルの三角比を理解出来ないバカには式変形は無理だよなwww >>595
高校生にわかりやすく例えるならここは大学受験板で算盤キチガイを隔離するみたいなスレだから
算盤での計算に馴染まないからそんな方法や答えは頭悪いww
とか喜んでる人を隔離してるんだ 高校生は飲酒してはいけないがフェラしてもいい。
プログラムしてもいいのも同じ。
>>591
シミュレーション結果
> mean(replicate(1e7,fcmf(100,100))==5)
[1] 0.0027196
道具が使えない碍児は200人集めて実験すんの? 発達障害プログラムキチガイ爺の発言集
一辺の長さが1の正77角形の高さを手計算する?
普通、プログラム書いて数値計算するだろ。
そうでないなら計算式を書いてみてくれ。
こういう計算してグラフを書かせる。
f <- function(n,print=FALSE){ # height of the polygon of side length 1
q=2*pi/n
r=cos(q)+1i*sin(q)
p=numeric(n+1)
for(i in 1:(n+1)) p[i]=r^(i-1)
H=abs(ifelse(n%%2==0,(p[1]+p[2])/2,p[1]) - (p[n%/%2+1]+p[n%/%2+2])/2)/abs(p[1]-p[2])
if(print){
plot(p,type='l',bty='l',axes=FALSE,ann=FALSE,lwd=2)
for(i in 1:n) segments(0,0,Re(p[i]),Im(p[i]),lwd=2,col=2)
}
return(H)
}
1辺の長さ1の正7角形の高さの厳密解を求めたら
こんな式になってしまった。もっと簡単にできるかもしれん。
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
発達障害プログラムキチガイ爺の発言集PART2
道具が使えないのはガイジ。
怒涛の計算力と根性があれば77角形の高さは計算できるぞ。
三角関数の計算は必要ないから理論上は手計算できるし、計算式も書けるけど複雑すぎて手作業では無理だね。
式変形もPCが出せるものはPCに頼る。
それができないのはプログラムを組んで数値解を出す。
知能が普通以上の高校生の場合
数学Iの知識のみで手計算で瞬殺
(1/sin(π/77)+1/tan(π/77))/2
所要時間30秒未満
プログラミングについては大学進学後に必要ならば学習すればよい
発達障害プログラムキチガイ爺の発言集PART3
面白い問題おしえて~な 32問目
http://2chb.net/r/math/1586230333/
883:132人目の素数さん 2020/08/02(日) 17:51:52.17 ID:pxJDvakc
O(n^α) ってなんですか?
大学初年度の微分積分学で学ぶ「ランダウの記号」すら知らない
計算機科学の分野では計算量を表し、アルゴリズムの評価に用いられる
数学Iの三角比すら理解していない事から考えると中卒なのは間違いだろう >>604
この答を出したら手書きで円がどういう形状になるか作図すんの?
普通はプログラムするだろ。
そもそも**の公式ってミニプログラムじゃん。
円錐角(母線と軸のなす角)がθの円錐側面の展開図を頂点を原点にy軸に対称に置く。
尚、円錐底面の円の展開は考えない。
円錐側面展開図上の点Aの座標を(p,q)とすると展開図を円錐化したときのAの三次元座標をp,q,θで表わせ。 数学Iレベルも分からない
もちろん大学で微分積分を学んでいない
中卒のプログラム爺
学歴コンプ&数学コンプ
劣等感から高校生を毎日煽らないと気が済まない哀れな発達障害のキチガイ爺
・プログラムキチガイ爺の場合
1辺の長さ1の正7角形の高さの厳密解を求めたら
こんな式になってしまった。もっと簡単にできるかもしれん。
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
・知能が平均以上の高校生の場合
数学IIで学ぶ2倍角の公式や半角の公式を使って簡単に式変形が出来る
与式 = 1/(2tan(π/7)) + 2(cos(π/7))^2/(4sin(π/7)) + 1/(4sin(π/7)) + (1-2(cos(π/7))^2)/(4sin(π/7))
= (1/2)*(1/sin(π/7) + 1/tan(π/7))
プログラムキチガイ爺は2倍角の公式や半角の公式が使えない事が分かる
この程度の計算でさえ機械に頼る発達障害の池沼爺
機械が出した答えを式変形する能力がない知恵遅れ爺
どうすんの、って、そんな力づくが必要に成り過ぎる問題自体が採用されねーよコンピューターおじいちゃん
その昔、コンピューターおばあちゃんって曲があったがコンピューターできないおばあちゃんへの差別とする声が浮上し放送されなくなった
(1) (x^2-7)a+(x-2)(bx+c)=3がxについての恒等式となるような整数a,b,cを求めよ。
(2)整式x^9をx-2で割ったときの余りを求めよ。
(3) 整数係数の整式f(x),g(x)に対し、f(x)~g(x)であるとは
f(x)-g(x)=(x^2-7)p(x)+(x-2)q(x)
がxについての恒等式となるような整式p(x),q(x)が存在するということであると定義する。
(i) (1),(2)を用いて、x^9~2であることを示せ。
ここまではできましたが、ここから先がわかりません。
(ii) 整数係数のすべての整式f(x)に対し、
f(x)~0 または f(x)~1 または f(x)~2 が成り立つことを示せ。
(iii) a,bを0以上2以下の整数とするとき、a~bであるならばa=bであることを示せ。
・中卒プログラムキチガイ爺の場合
1辺の長さが1の正何角形の高さの計算なら高校数学なんだ?
正777角形だと247.326になったけどあってるかw
とプログラムを組んで数値計算
・知能が平均以上の高校生の場合
まず高さを
(1/2)*(1/sin(π/777) + 1/tan(π/777))
と出す
その後、|θ|が十分小さいとき
sinθ≒θ
tanθ≒θ
と近似出来るので
(1/2)*(1/sin(π/777) + 1/tan(π/777))
≒777/π
≒777/3.1416
≒247.326
と同じ値を出せる
または
正777角形の外接円を考え
正777角形の一辺の長さ≒中心角が2π/777である扇形の弧の長さ
正777角形の高さ≒外接円の直径
と近似
外接円の半径をrとすると
中心角θ = 2π/777である扇形の弧の長さは
rθ≒1
r≒1/θ
正777角形の高さ≒外接円の直径より
2r≒2/θ≒777/π
となり同じ結果を出せる
数学IIIの1次近似式を学んでいれば解ける問題
数学Iの三角比すら分からなかった中卒のプログラムキチガイ爺には理解出来ない内容
>>605
>大学初年度の微分積分学で学ぶ「ランダウの記号」すら知らない
ここ高校数学のスレなんだが。
自爆してね? 進学校や塾・予備校では数学IIIでランダウの記号を習う場合もある事を知らない中卒プログラムキチガイ爺
大学レベルは言うまでもなく、高校数学Iレベルの知識すら持っていない中卒プログラムキチガイ爺
学歴コンプ&数学コンプのキチガイ爺
毎日スレ違いの問題を書き込みドヤ顔して憂さ晴らしする劣等感丸出しのキチガイ爺
>>613
θが十分小さいときのsinθはどうやって計算すんの?
それが手計算できなきゃθで近似するのはインチキでカンニングだね。 >>582
(p,q) がデカルト座標なら、頂点Oを極とする極座標(r,φ)に移す。
r = OA = √(pp+qq),
φ = arctan(q/p),
母線の長さがr、”円錐角”がθの円錐面に移す。
底円の半径が r sinθ,
底円の周長が 2πr sinθ
-π sinθ ≦ φ ≦ π sinθ
軸まわりの方位角 は φ/sinθ
A = (r sinθ cos(φ/sinθ), r sinθ sin(φ/sinθ), r cosθ) >>612
f(x)を(x-2)で割ることで
f(x)=(x-2)h(x)+f(2)とできる
ここでh(x)はある整式、f(2)は整数である
f(2)を3で割ってf(2)=3k+aとできる
ここでkはある整数、aは0,1,2のどれかである
3=(x^2-7)(-1)+(x-2)(x+2)に注意すると
f(x)-a=(x^2-7)(-k)+(x-2)(h(x)+kx+2k)
となりf(x)~aであることがわかる
いまa~bであるとすると
a-b=(x^2-7)p(x)+(x-2)q(x)
であり、両辺にx=2を代入することで
a-b=-3p(2)を得る
よってa-bは3の倍数でありa=bとなる lim_[θ→0] sin(θ)/θ = lim_[θ→0] tan(θ)/θ = 1
を証明せよ。
|x| ≦ π/4 のとき、不等式
|x - sin(x)| ≦ |tan(x) - x| ≦ x^2
は成り立ちますか?
成り立つとすれば高校数学の範囲内で証明できますか?
>>621
教科書に載っている公式の証明は教科書を読みましょう。
実際のところ三角関数の定義の仕方によって証明の内容が異なりますので、「まず定義を述べよ」となります。
>>622
成り立ちます。高校範囲で十分証明できます。
奇関数だから 0≦x≦π/4 で x-sin(x)≦tan(x)-x≦x^2 を示せば十分ですが
各不等式ごとの差の評価について、1つめの≦は1階導関数、2つめの≦は2回導関数まで調べれば十分のようです。 >>622 (左)
0<x<π/2 で考える。
まずは正攻法で tan の半角公式
tan(x/2) = sin(x)/{1+cos(x)},
を使おう。
{1-cos(x)}{x-sin(x)} > 0,
2sin(x) - {1+cos(x)}x = 2{1+cos(x)}{tan(x/2)-(x/2)} > 0,
辺々たすと
{sin(x) + tan(x) - 2x}cos(x) > 0,
cos(x) >0 より
x-sin(x) < tan(x)-x,
微積分を使うなら・・・・
2{x - sin(x)} < tan(x) - x,
も出る。AM-GMより
cos(x) + cos(x) + 1/cos(x)^2 > 3,
xで積分して
sin(x) + sin(x) + tan(x) > 3x, (0<x<π/2)
これを "Snellius-Huygens の式" と云うらしい。
(注意) 便利な道具は人間を脆くする・・・・ >>622 (右)
0<x<1 で考える。
(1+x)cos(x) = (1+x){1 - 2sin(x/2)^2}
> (1+x)(1-xx/2) = 1 + (1-x)x(x+2)/2 > 1,
∴ (1+x)x > (1+x)sin(x) > sin(x)/cos(x) = tan(x)
∴ tan(x) - x < xx, >>622
まずは、作図

道具が使えないアホには無理だが。 描画範囲を広げてみた。

チョト改良
0<x<1 で考える。
(1+xx)cos(x) > (1+xx){1 - 2sin(x/2)^2}
> (1+xx)(1-xx/2) = 1 + xx(1-xx)/2 > 1,
(1+xx)x > (1+xx)sin(x) > sin(x)/cos(x) = tan(x)
∴ tan(x) - x < x^3,
皆さんありがとうございます
>>621は確かに教科書に載っていましたね、すみません
>>622よりも強く、 |x| < 1 のとき
|x - sin(x)| ≦ |tan(x) - x| ≦ |x^3|
が成り立つんですね
もしこの不等式が使えるなら>>621は明らかですね
この不等式を使えば、例えば |x| < 0.05 において
|x - sin(x)| ≦ |tan(x) - x| ≦ (0.05)^3 = 0.000125
となるので、これによって sin(x) と tan(x) の値を直接計算しなくても、
sin(x) と tan(x) を x で近似したときの誤差は高々 0.000125 程度だとわかるわけですね 0≦s≦1, 0≦t≦1 のとき, s^2+4st-2t^2-3s+2≧0 を示せ。
この問題で、左辺をtの2次関数f(t)とみて、上に凸な放物線なので
0≦t≦1でのfの最小値はf(0)かf(1)だが f(0)=(1-s)(2-s)もf(1)=s(1+s)も0以上なので、ok.
としたのですが、
もっとうまい式変形で一発で示す方法はないすか?
すみまんせん訂正します。
× 方法はないすか?
○ 方法はないですか?
>>599
なるほどなぁ
そのスレ違いを指摘してる人たちが板違いを認識してちゃんと適切な板にスレ立てれば解決だな
スレ違いを指摘できる程度に理性的に考えられると自認してるならそういう行動をしてほしいね
わざわざこの荒らしを隔離することが目的のスレでルールなんて言うことが馬鹿げてるんだな まぁ高校内容のことを質問するくらいなら許容して全く問題ないと思うけど、高校生のためのスレにしたいならさっさと他所いけとは思う
高校範囲外の知識についてギャーギャー言ったりなるべく高校範囲の知識で解くよう努力するのは数学の話ではないしバカバカしい
まぁ高校範囲外のことを解答するくらいなら許容して全く問題ないと思うけど、プログラミングオナニースレにしたいならさっさと他所いけとは思う
理論的に解ける問題をプログラミングで解くのは数学の話ではないしバカバカしい
人を真似して煽ったり、そういうことばかりしてるから荒らしの隔離スレだって意見がなされるんだよ
プログラミングオナニーの擁護なんてしてない、理屈がおかしいと言ってるのに、なぜ煽ったり極端な表現ばかりするのか
荒らしだからでしょう、ここは誰にも正当性がなくアホが罵り合うだけの隔離スレだって自覚してるからまず煽るに決まってる
アホ高校生が集うゴミ溜めにようこそ
ここは初めてか?力抜けよ
人を荒らし扱いするのは結構だが、荒らしはスルースルー言って全然スルーしないんだな
荒らし扱いされてしょうがないでしょうと言ってるんだよ
自分が反論しやすいように曲解し、解釈し、俺が言ったわけではないことを言ったことにする
本当に論理を大事にしないんだな
>>640
お前も俺も間違いなく頭おかしいこと言ってる荒らしだからなー
反応してるやつはバカwwww >>634
> まぁ高校内容のことを質問するくらいなら許容して全く問題ないと思うけど、高校生のためのスレにしたいならさっさと他所いけとは思う
よく意味が分かんないんだけど。
高校の内容を質問するのを許容とかw
許容しない理由があるのか?
それに高校生のためのスレにしちゃいけない理由が分からない。
高校数学をやっている人の多くは俺みたいな高校生じゃないのか?
そのレベルに合わせて答えてもらわないと困るんですけどw
大学レベル内容で答えられても困るし。
そんな事をされるとオッサンが高校生相手にドヤ顔してる風にしか見えない。 >>627
例えば、この爺さん。
一々煽らないとレス書けないのか?
高校生にとっては道具を使ってグラフを描く事よりも、道具を使わずにグラフを描く方が重要なんですけど。試験ではパソコン持ち込めないし。
この爺さんは道具無しではグラフも描けないんだろうけど。
しかもそのグラフ、証明には殆ど役に立たないしw >>631
十分上手いやり方だと思う
Wolfram大先生によると境界が双曲線になるとのことなので、
とりあえず標準化してみた
s^2+4st-2t^2-3s+2 = (2/5)(2s + t - 3/2)^2 - (3/5)(s - 2t + 1/2)^2 + 5/4
うーん… >>644
手始めに>631のグラフを手書きしてみてくれ。 >>631
十分上手いやり方だと思う。
左辺をf(t)とおくと
f(t) = f(0) + 2t(2s-t), f(0)=(1-s)(2-s)≧0,
f(t) = f(1) + 2(1-t)(1+t-2s), f(1)=s(1+s)≧0,
加重平均して
f(t) = (1-t) f(0) + t f(1) + 2t(1-t) ≧ 0,
かな >しかもそのグラフ、証明には殆ど役に立たないしw
証明って何が自明かで主観がはいるからなぁ。
>366みたいにグラフで明らかという人もいるしね。
>631
グラフにより明らかw

爺さんが朝から道具でグラフを作成w
この爺さん、正多角形の高さをパソコンを使わないと求められないらしいね。かなり残念な知能しか持ってないだね。
そんな人でも使える道具ならちょっと練習すれば大抵の人は使えるんじゃないの?
凄いのはこの爺さんじゃなくて、残念な知能の人でも使えるアプリの方だねw
パソコンでグラフを書いただけで最小値とかの証明になんですか?
パソコンは細かい点を沢山プロットして滑らかに繋いでいるだけですよね?結局飛び飛びの値を扱ってるだけですよね?
点と点の間についての情報は何もないですよね?
それなのにグラフを見て最小っぽい点を最小って決め付けていいんですか?
増減表を書いてその点が、例えば極小かつ最小って感じで調べる必要があるんじゃないんですか?
基地外爺さん以外の人、教えて下さい
数Iが出来ない爺さん顔真っ赤にしてレスを書き込んでるんだろうなw
>道具を使わずにグラフを描く方が重要
と言っている椰子がグラフを書くのを待っているんだが。
基地外爺さん発狂中ww
1変数の関数のグラフの話をしてたのに、何故か2変数の関数のグラフの話をする爺さんw
ボケがはじまってるのかな?アルツハイマー?
ボケてるから朝飯を3回くらい食っていそうw
A,Bをどちらか選ぶとき無作為 に選んだ 400 人中 100 人が,A を支持すると回答した.そのとき,A の支持率 p について,以下の問いに答えよ
1. 標本比率(標本平均) x の値を以下の中から選
択せよ
(1) 0.2, (2) 0.25, (3) 0.5, (4) 0.75, (5) 0.8
2. A の支持率 p の 96.6% 近似信頼区間を求めよ
(1) [0.247705,0.252295], (2) [0.2075648,0.2924352], (3) [0.2041007,0.2958993],
(4) [0.06022382,0.4397762], (5) [0.04473188,0.4552681]
1が0.25はわかりますが2ばんめがわかりません
学術の巨大掲示板群 - アルファ・ラボ http://x0000.net
数学 物理学 化学 生物学 天文学 地理地学
IT 電子 工学 言語学 国語 方言 など >>631
十分上手いやり方だと思う。
左辺をf(t)とおくと
f(0) = (1-s)(2-s) ≧ 0,
f(1) = s(1+s) ≧ 0,
f "(t) = -4 < 0 だから f(t) は上に凸で
f(t) ≧ (1-t) f(0) + t f(1) ≧ 0 (0≦t≦1)
かな f(0) と f(1) の値を計算するだけで証明できるなら十分エレガントだよね
>>645(自分のレス)のように(大学レベルの知識を使って)標準化してもあまり役には立たない
図形的に考えるなら、 s-t 平面上の双曲線(を回転&平行移動したもの)で囲まれた領域が
条件 ≧ 0 を満たすことになるが、その領域に [0, 1] × [0, 1] が含まれることは明らかではないと思う 
中学数学で申し訳ないんだけど弟に聞かれてわからんから教えてもらいたい
頭固くなりすぎなんかな >>667
中学数学のスレもあるだろうとは思ったけどなんか見つからなかったわ
スレチすまん >>666
[7] 図の x°を求めなさい。
上A、左下B、右下C、中央D とおく。
∠B = ∠C = 40°
∴ AB = AC = BD = 1
BC = 2cos(40゚)
CDの傾きから
tan(40゚-x゚) = sin(20゚)/{2cos(40゚)-cos(20゚)} = 1/√3,
40-x = 30,
x = 10. 中学の問題に高校数学の知識使うのはルール違反だって荒らしたちに言われるぞ
>>664
〔Jensenの不等式〕
・大関:「不等式への招待」(現代数学ゼミナール6)近代科学社 (1987)
3章 p.96~101
・佐藤淳郎(訳)「美しい不等式の世界」朝倉書店 (2013)
§1.5 凸関数 p27~34
・安藤哲哉:「不等式」数学書房 (2012)
§1.2 p.7~10 >>666
プログラムして解いてみた。
intsect <- function(a,b,c,d){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(a2-b2)/(a1-b1)
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(c2-d2)/(c1-d1)
if(p==q) return(NA)
else{
x= ((p*a1 - a2) - (q*c1 - c2))/ (p-q)
y= p*x - ( p*a1 - a2)
x + 1i*y
}
}
plot(NULL,type='n',xlim=c(0,2),ylim=c(0,2),asp=1,ann=F)
u=pi/180
A=cos(20*u)+1i*sin(20*u) ; pt(A,'A')
seg(0,A)
B=cos(40*u)+1i*sin(40*u) ; pt(B,'B')
seg(0,B)
seg(A,B)
abline(h=0,col=8)
Arg(A-B)
f <- function(x) tan(-40*u)*(x-Re(B))+Im(B)
curve(f(x),add=T,col=8)
C=intsect(0i,1+0i,B,1i*f(0)) ; pt(C,'C')
seg(C,A)
(Arg(A-C)-Arg(B-C))/u
実行すると
> (Arg(A-C)-Arg(B-C))/u
[1] 10 >>672
プログラムを組んだので20°を変化させたときのxの値を出してみた。
angle x
1 1 0.9981746
2 2 1.9854507
3 3 2.9511971
4 4 3.8853008
5 5 4.7783870
6 6 5.6219978
7 7 6.4087218
8 8 7.1322723
9 9 7.7875169
10 10 8.3704628
11 11 8.8782051
12 12 9.3088475
13 13 9.6614033
14 14 9.9356860
15 15 10.1321948
16 16 10.2520025
17 17 10.2966480
18 18 10.2680381
19 19 10.1683593
20 20 10.0000000
21 21 9.7654839
22 22 9.4674141
23 23 9.1084267
24 24 8.6911525
25 25 8.2181878
26 26 7.6920702
27 27 7.1152613
28 28 6.4901331
29 29 5.8189594
30 30 5.1039094
31 31 4.3470441
32 32 3.5503153
33 33 2.7155651
34 34 1.8445277
35 35 0.9388310
きりのいい答になるのは20度の時だけだな。 この三角形の面積を求めよ、という有名な問題。
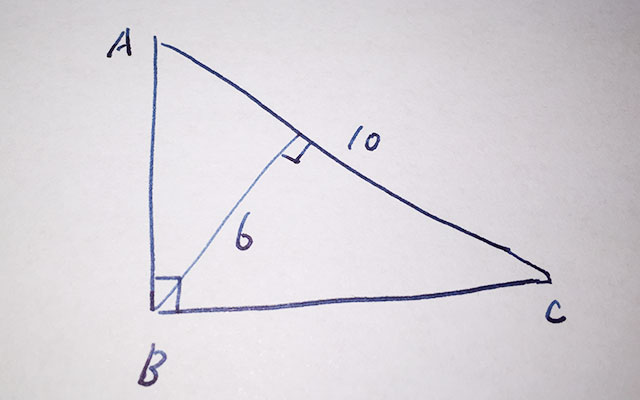
>>675
そんなのが有名問題なのか?
存在しない三角形の面積など求めようがないと思うのだが。 >>676
マイクロソフトの入社試験。
手書きでグラフを書く修正があると気づかないんじゃないかな?
道具を使ってこんな風に作図した方がいいよね。
高校生に飲酒は禁じられているが、プログラムもフェラも禁止されていない。

AB・BC = 60, AB^2 + BC^2 = 100
(AB + BC)^2 = AB^2 + BC^2 + 2AB・BC = 220 ∴ AB + BC = ±2√55
(AB - BC)^2 = AB^2 + BC^2 - 2AB・BC = -20 ∴ AB - BC = ±2√5 i
∴ AB, BC = √55 ±√5 i
存在するじゃん
>>677
飲酒が禁じられる条件は20歳未満かどうかであって高校生かどうかは関係ない 青チャートと赤チャートってどう違います?
どっちがどういう人にオススメなんでしょうか?
スレチな内容かもしれませんが教えて頂けると助かります
>>679
これってプログラムキチガイ?
長さが虚数になってるじゃんw >>679
球面上で考えたら存在しそうだな。
よく知らんけど。 >>674
使える道具はたくさんある方が( ・∀・)イイ!!
道具が使えない椰子はこういうのは手計算するのだろうか? >>679
プログラムキチガイ
新たな伝説!!
作図不可能な三角形に対し
AB, BC = √55 ±√5 i
存在するじゃん
と三角形の存在を主張!! 入社試験で「今からプログラム書くので少しお待ち下さいね」っていってPC取り出すんかな
>>686
俺じゃないけどな。
でも、あの数字は何を表すのかは興味があるな。 >>687
最近はスマホでもRも使えるしGeogebraも使えるよ。
道具が使えるかどうかが人間とサルの違いだという人もいる。
サルに近いやつはマウント・マウントと繰り返す。 >>689
ってことは、スマホは取り出すってこと? >>690
禁じられてなければいいんじゃないの?
女子高生のフェラと同じ。 >>673
俺も中学数学でどうやって解くのか知りたい。 道具って素晴らしいよな
数学Iレベルの問題が分からないバカでも使えるんだからw
この草生やしてプログラム荒らしに粘着してる荒らしもわかりやすい名前あったほうがいいよな
と言っても、自分の分からない話題出されることが気に食わなくて草生やして煽りまくるというただのよくいる子供のムーブだから特徴が難しい
>>695
まず、
>666を中学数学で解いてみてくれ。 >>694
あれ?俺はオマエにレスアンカー付けてないんだけどw
数学Iレベルの問題が分からないバカって自覚あるんだwww
それにプログラミングは大学入ってから覚えればいいだけだしなw
本当は>>679の書き込みもオマエだろw >666は数値を変えて類題を試験問題にするのは困難であることがプログラムによる計算で判明したな。
道具を使えない椰子はどうやって計算すんの?
>>697
最初から答を知っていたから、俺じゃないけど。
あの虚数がどういう意味なのかは興味があるな。
>それにプログラミングは大学入ってから覚えればいいだけ
高校生に禁じれられているわけでもない。
女子高生のフェラと同じ。
Geogebraのユーザー評価に高校数学で立体グラフを書くのに時間の節約になって考察が深まりました、と書いてあって
道具が使える高校生は利用するよね。
マウントガ イ ジはそうではないらしいが。 今日も今日とて怪獣大戦争
高校生はやく夏休み終わって消えてくれねーかな……
>>700
何コイツ
高校生でもないのにこのスレに居着いているのかw 学問ジャンルの数学板に高校数学とかいう学問ではなくルールの範囲内で答えを見つけるクイズしか出来ないだけの子供がいるらしい
板違いだなぁ~
高校数学は学問でなく板違いらしいなので次スレは不要だね、立てられたら削除申請しようね
削除申請まともに機能してるならそれでいい思うけど残念ながら
ルールの範囲内で解かなきゃいけないとなったら学問ではなくクイズだろうな
荒れてるし次スレ立てなくて良いんじゃない?
それか>>1に高校範囲の問題をルール無用で解くスレである旨を記載するか >>707
まず、
>666を中学数学で解いてみてくれ。 >>691
入社試験の面接でフェラしたら秘書として即採用かもしれんなww >4で
プログラムやグラフソフトが推奨されているんだが、俺様ルールを強要したがるのが
道具の使えないマウント猿じゃないの?
>>710
あーそれは質問する前に自己解決するためのツールと質問する際に図形を描画するためのものだ。
テンプレはすべて質問する人向けのもので、回答には一切言及していないよ。 >>711
自己解決できずグラフも描画できないマウント猿がいるわけだが。 そもそも数学的に正しい回答であれば論理的には何でもいいのでそこに言及する必要もなかった
ただ勘違いして高校数学の範囲内で解く、あるいは解けたほうがいいと勘違いして無自覚な荒らしになる人がいるなら
>>706
と近いことをテンプレに書いてもいいかもしれない >>713
それなら分からない問題スレに一本化すればいいだけだろ
わざわざ高校数学ってタイトルにあるんだから出来るだけ高校数学の範囲の知識で解けよバカwww
因みに高校範囲外を一切使うなとは言ってないからな
発展的内容でちょこっとくらい大学1年くらいで習う内容を書いてくれるのは有り難い
プログラムキチガイみたいに初めからパソコンでないと解けないようなモノはお断り >>708
コイツ思った通りバカだわ
補助線引けば解けるのにwww
正多角形の高ささえパソコンを使わないと求められない池沼だしなwww
数学Iレベルの問題さえ解けない池沼が何を言っても無駄だわwww >>716
じゃあ、20°じゃないときの一般式を書いてみてくれ。 >>716
別にパソコン使って求めるのがなにかまずいか?
円錐の展開図上に置いた輪ゴムの見取り図とか手書きじゃ無理。
水洗トイレとトイレットペーパーがあるのに
野糞が一番と言っている道具を使えないガイジだなぁ 数学Iを理解していない池沼でも使えるプログラミング言語は最高だなwww
使えると言っても解説本や解説サイトに書いてあるプログラムを利用してるだけでしょ
それをちょこっと改変したプログラムを動かして、その結果を毎日書き込んで悦に入る中卒ジジイwww
全然マウント取れてないから
逆に見下されているよ
俺だけでなく他の奴ら全員からwww
>>675の画像の求積問題の何が難しいんだ?プログラム組む前に即決できるだろ、計算苦手な人間でも暗算できる。 テンプレに追加したる文言のたたき台出しとく
言葉遣いや表現など議論してくれ
このスレは数学的解答を聞く場所です
高校数学の範囲内での解答を得るスレではありません
定期テスト、大学受験などに配慮した解答を望む場合、別板に移動お願いします
テンプレ変更なんていらん。
そもそも夏厨が山ほど沸いた状況では議論にならん。
そういう判断は平常運転時にすべし。
>>722
個人的には住み分けが必要ないと思っているけれど、立てるなら
>>721
みたいな文言入れておけば勘違いしたお客様が減るかなと思う
あとそちらのスレには俺は行かないから知らないのだが、そちらのスレが高校数学を容認してるかどうかについて知らないと住み分けについてはなんとも言えないかな >>723
こういう時でもないと忘れられて議論にならないとも……
わかりやすい夏厨は今の通りスルーするとして、議論だけでもやっておけば夏が終わって消えた頃にはルールに付け加える下地ができるのではないかな 住人が決めたルールよりも
スレタイが表現しているものの方が強いと思うけど
>>728
今回のテンプレは束縛ではなくて、高校数学に束縛されない、という提言だから賛成してる
俺も束縛なら賛成しない >>722
問題が高校数学で理解できる範囲でいいんじゃないの? 個人的にはプログラムの人はイナと同様ズレたこと言ってるだけなのでスルーすればいいと思ってる
ただプログラムに粘着してる人が高校数学の範囲内であることにこだわってて、それへ同意する人も一部見られるので、今後自由に数学的発想することが許されなくなることを危惧してる
まんまと議論ズラされてんな
高校範囲外か範囲内かが問題じゃないだろ
プログラムはそもそもプログラムが正しいか判定できないし、かと言って長いコードをコピペされるのもスレが見にくくなる、ていうのが問題点なわけで
>>732
>今後自由に数学的発想することが許されなくなることを危惧してる
以前も似たような文章を見たような気がするが、そういうのはどうせ杞憂に終わるから心配ない
大学以上の知識を使って回答する人もいれば、高校数学の範囲内で回答する親切な人もいる
質問者が理解できるかどうか気にしない人はどうせルールなど気にしない >>733
議論ずらしって前にも言ってる人いたけどさ、違うんだよ
高校範囲内か範囲外かを気にしてる人がいて、このスレは高校の範囲内であるべきだと思ってる人がいるんだよ
だからそこの誤解をテンプレに付け足すことに問題があるとは思えない
プログラム荒らしのやってることについて、スルーする以上のなにか議論があるならやってくれればいい
それとは別に高校の範囲外を排除しようとする意見を肯定するわけにはいかない >>734
ルールを気にしない、ではなく、荒らし扱いすることがおかしい >>736
別に大学レベルの回答を荒らし扱いする人なんていないぞ >>737
ならそのあたり前のことを勘違いして無自覚な荒らしになってしまう人もいるので、薬になるか分からないが毒にならない文言をテンプレにとりあえず入れてみたらと思ってるよ テンプレに解答は自由であるというような文言を入れること自体に反論がないなら入れていいのではと思う
ぶっちゃけ反論なんてないしテンプレに入れたらいいと思うよ、それで解決するかはしらんけど、入れて何も困るもんではない
議論でスレ埋められるくらいならとっととテンプレに入れるで結論にしたらいい
とんちんかんな回答をする人はテンプレなんて読んでないよね
だって既に書いてあるんだから
>・まずは教科書、参考書、web検索などで調べるようにしましょう。(特に基本的な公式など)
→質問者は高校生であると想定されている?
大学以上なら「参考書」という用語はまず使わない
>・回答者も節度ある回答を心がけてください。
→「節度ある回答」
>>741
人の否定をするばかりでなく、まずあなたの意見をちゃんと表明して欲しいのだけど、このスレはそもそも高校の範囲内に絞るべきだと思ってるということ? >>735
いずれにしても過度なプログラム解答がoutってことなら納得 >>743
今いるプログラム使いたがる人ならそれは当たり前でしょう
使い方を過った道具は解答にすらなっていません
その上で、高校数学の範囲内に、なんて意見については釘を差しておく必要があると考えてます >>742
テンプレと>>741の通り
まずスレタイから、質問の条件は
(1) 高校数学の範囲内
または
(2) 質問者が高校生
の少なくとも一方を満たすこと
ただし、条件(1)において、問題そのものが高校数学の範囲内かどうかを問う等、多少の例外は認める
また、(2)においても、明らかに高校数学の範囲内の質問でない場合はスレチとする
(分からない問題スレ等、他に適切なスレがあるので)
ここまではおk?
あとは「節度ある回答」を各々が解釈して、適切に回答すれば良い
質問者が求めていれば大学レベルの回答でも不適切というわけではないし、
もちろん「高校数学の範囲内では解けない」という回答もおk
要するに回答が適切かどうかは質問者に依存するので、一概には言えない 分か問スレと変わらねぇんじゃ高校数学の質問スレじゃねぇだろ、日本語が分からないのか?
わざと大学数学の問題や自作の思いつき図形問題や積分問題を高校数学だという装いで書かれることがアレなんだよな
後者は他の問題スレでもなかなかのウザさがある
これに関して悪いとは言えないが、この手の問題はすぐに簡単に解けないのが作れてしまうし、こういうのに限って変なのが珍解答を繰り返してるイメージ
>>745
このスレでは数学的な解答が得られます
ただしそれが高校範囲内に留まるとは限りません
定期テスト、大学受験などに配慮した解答のみを望む場合、別板に移動お願いします
こんな感じのテンプレでいい? テンプレ追加でくだらない制限だけはやめてくれ、俺達は数学はやっていても、指導要綱や数学教育のプロではない
>>749
制限ではなく、制限してないことの確認だから安心して
このテンプレ追加で駄目になることは、「高校数学の範囲外だからという理由で回答にネガティブな意見を与える」ことであって、回答自体はむしろ自由であることの確認 テンプレ追加に賛成
ただもう700レスだから、とりあえずテンプレ候補として>>5あたりに置いておいて、次のスレでも議論したい人は議論したらいいんでない
テンプレ追加が駄目な説得力ある意見がそこで出るかをまって結論したらいい >>748
なぜ>>745を読んでそうなるのか
>>745は要するに「既にスレタイとテンプレに書いてあるじゃん」ってことだぞ
あとそれだと高校生が質問しにくくなるんじゃね
分からない問題スレでいいじゃんってことになりそう
隔離スレとしての機能を果たせなくなって他のスレに迷惑がかかるかも >>752
より適切な板に適当なスレを立てて誘導すればいいと考えることがそんなにおかしい?
分からないスレにもし高校数学の質問があふれて迷惑になるならこちらに誘導してもらえばいい
その上でそのスレに適切でないなら別板に誘導したらいい
スレタイとテンプレ見て、私のテンプレ案見て、あなたの意見見てその上で特におかしいところは感じないけどそこは多分私の頭が悪いせいなのでそこを言語化してほしい >>753
その誘導を君が最後まで責任もってやってくれるのならそれでも構わないが、
無責任にテンプレを追加して問題が起きたら誰かが対処してねという態度ならダメ
>隔離スレとしての機能を果たせなくなって他のスレに迷惑がかかるかも >>754
じゃあテンプレ追加しなくて問題起きたときの責任お前が取れよ >>754
いやいやいや……
さすがに暴論……
テンプレやスレルールってそんな責任のもとで行われるものではないでしょう……
5chにあふれるテンプレはそんな認識のもとでは作られてないし、そんな認識では作れない…… >>756
>>752に書いたが、俺の意見は
>「既にスレタイとテンプレに書いてあるじゃん」
だから、そのようなテンプレを追加する必要性を感じない
>>745に異論はないんでしょ? >>757
>>754との整合性がわからない
分かりきってることを改めて書く必要はないということ?
あなたの言いたいことが伝わらない…… テンプレ追加しなかって問題起きたときの責任は>>757が取るということなんだから
とりあえずテンプレ追加無しでやってみたらええやん
問題起きたら、全員が満足とまではいかなくても全員が納得できるくらいの対応は>>757が責任持ってしてくれるでしょ
それで納得できる対応がなければ、テンプレ追加ってことで >>758
テンプレを追加することによる悪影響は>>752に書いた通りで、容易に想像がつくが、
テンプレを追加しないことによる悪影響は特に思いつかない
あるなら教えてくれ こういう、自分の一本筋の通った意見を明示してそれに基づいた意見を述べるのではなく、相手の意見への否定を基礎にしてる人は、基本的には議論ではなく感情的に許せないものがあることが多い
たぶん今回の場合、本質的には高校数学の範囲外が嫌だ、見たくないという感情を出発にして論理建ててる
>>761
高校数学の範囲内でないという理由で否定する人が現れる
また、そのことについてフォローがしにくい
馬鹿馬鹿しいからテンプレ改変に関わる責任について言及したくはないが、そのフォローをあなたはする気があるということだろうか >>763
>高校数学の範囲内でないという理由で否定する人が現れる
>また、そのことについてフォローがしにくい
テンプレ読めでおkじゃね?
「節度ある回答」かどうかを議論すべき >>764
そのフォローを貴方はしてきてないでしょう
私は時々言ってきたが >>765
俺は別にフォローする必要がないからな
大学レベルでも「節度ある回答」の範囲内ならおkでしょ >>766
一般論として高校数学の範囲外であることを理由として、節度ある回答でないものを否定している場合、高校数学の範囲外であることは一般論としてスレ違いにならないというフォローは当然に必要
節度ある回答でない、テンプレ読め、などという理論によって高校数学範囲外であること自体は問題でない別の問題があるんだと諭すフォローは見た覚えがない >>765
まぁこれまではID:cYInbD7iがフォローする義理も無かっただろうからな
でもテンプレ追加しないことを主張した以上、今後はID:cYInbD7iが責任持ってフォローしてくれるよ
相手には
>無責任にテンプレを追加して問題が起きたら誰かが対処してねという態度ならダメ
と言っときながら、自分はテンプレ追加しないことを主張してその責任も取りませんなんてことはまさか言わないやろう >>762
お前の論法、気付かれなければ言った者勝ちの尤もらしい空論だな。現に逆の立場からも通用する。
↓
こういう、自分の一本筋の通った意見を明示してそれに基づいた意見を述べるのではなく、相手の意見への否定を基礎にしてる人は、基本的には議論ではなく感情的に許せないものがあることが多い
たぶん今回の場合、本質的には高校数学の範囲限定が嫌だ、見たくないという感情を出発にして論理建ててる >>768
どうせやらないだろうからテンプレの議論をしたいが…… >>767
うん?
ちょっと日本語が難しい
>高校数学の範囲外であることは一般論としてスレ違いにならないというフォローは当然に必要
そうか?
そんなフォローしなくても大学レベルの回答がなくなったりはしないだろ
フォローしたいとしてもテンプレの後ろ盾が必要なほど深刻な問題とは思えない
「節度ある回答」以外は荒らし、で十分だと思うが
節度ある大学レベルの回答は批判されてないでしょ >>771
節度ある大学レベルの回答についてもたぶん俺とあなたで乖離があると思う
大学以上の知識を必要最低限にすることが必要だと俺は思ってないが多分あなたはそうだよね
だから俺は節度ある、なんてのは「あらしでなければいい」という意味でとってる
あなたは、節度あることが荒らしでないことの条件と解釈してるのでは?
そこは我々二人のみではなく意見を聞きたいね
そもそも節度の意味がテンプレからは読み取れないのでそここら論理的な結論は得られない 回答がなくなるとかどうではなく高校数学の範囲外なら駄目みたいな意見が蔓延るだけでうざったいしそこはフォローしてほしいわ
してくれないならテンプレいれろ
>>772
ふむ、確かに「節度ある回答」とは何かについては議論の余地があるな
>そこは我々二人のみではなく意見を聞きたいね
それはもっともなんだが、今は荒らしが常駐しているのでおすすめできない >>752
かけてもいいけど、高校生が質問しにくくなることはないと思う
言われるまでテンプレ読まないから
よほどテンプレに入れないことで回答にケチつくほうが問題ある 論点まとめ
私:大学以上の話を好きに使う権利はあるので一般論として大学以上を範囲外とする意見には指摘を入れるべきで、根拠をテンプレに入れたほうがいい
ID:cYInbD7i:大学以上の知識は必要最低限に留めるべきでそれを行ってないプログラムの人への批判は節度ある回答でないことも踏まえての批判だから指摘する必要はない
訂正あればお願いします
他の意見は訂正を踏まえてお願いします
>>776
自分の意見のほうも突っ込みやすい表現にしてるあたり好感
俺がテンプレ入れろ派だからかな いやテンプレ入れて不都合ないから入れておいていいでしょ
不利なまとめ方すんな
>>666
座標上で作図すれば誰にでも求まる。
手計算は面倒くさいから複素平面上で偏角使っての計算をプログラムでさせただけ。 >>776
>大学以上の知識は必要最低限に留めるべきで
ちょっと違うかな
同じだろって思うかもしれんが
テンプレに「・回答者も節度ある回答を心がけてください。」という文言があるので、
「節度ある回答」の範囲内なら大学レベルでもおkだと思っている
「節度ある回答」とは何かについては議論の余地があることは認める
あと後半については俺は何も言及していないぞ
捏造はやめてね >>780
フォローしない理由について解釈してみたが違ったか
ならプログラム粘着の人が一般論として大学以上の知識を否定してることについて意見を頼む >>781
荒らしについて言及することはあまりしたくないんだが…
まあ今このスレで罵り合っているやつらは大差ないでしょ
そんなやつらの言うことは気にするな
俺は時々現れるエレガントな回答も好きだし、
それに高校レベルの別証明を与えるのも好きだから ID:cYInbD7iはテンプレ入れないことを根拠付ける意見にはなってないのでは……
入れても別にいいんじゃないという結論に落ち着く気がする
テンプレ入れといたら?
>>721がテンプレ追加しようぜって話に出して、50レス以上もあれやこれやレスがついて議論になって、全然まとまる気配もない。
普通、年単位で変わってないテンプレに手を加えるってのはかなりの大多数が賛成するような内容でないとうまくいかんのや。
変えたテンプレについて、スレ本来の役割そっちのけで新しいスレでも議論が続きまくることになるからな。
どっちが正当性があるとか妥当とかそういう話ではないんや。賛否が両方ある時点で変えるべきではない。
よっぽど誰がどう見ても賛成しかありえんだろって状況以外では、前例踏襲で変更を嫌うのが日本人の慣例だ。 今回の場合、荒らしシンパの夏厨が否定してるだけでしょ
夏厨いなくなりゃテンプレ入れられるだろうし候補にしとこうや
匿名掲示板だと多数派工作って簡単にできるからなあ
荒らしがいるときはこういう議論はしちゃだめなんだよね
>>786
俺が多数派工作してるとか、あるいは俺が荒らしの自演と疑ってると?
正直今いるあらしはどちらも自演するようなタイプには見えないが……
何にしても論敵がいる状態で印象論で語るのは人としてどうかと >>787
落ち着いて、君の事じゃない
ただ、テンプレに入れると都合が良いやつがいるだろう?
一つ言えるのは、今のこのスレの単発IDは信用できないってこと
先日の出来事を知らない? >>788
テンプレ入れて都合がいい人もまぁいるし、単発IDが信用できないのも分かるが、大事なのは誰が言ったかではなけ何を言ったかだ
明らかにおかしい意見を単発IDが量産して荒らしてるならともかく、今単発IDの全部が全部おかしい意見で聞くに値しないとは思ってないし単発が自演だとしてそのことが議論の本筋に影響与えてるとも思ってない >>789
概ね正論だと思うが一点だけ
人間は、自分に都合の良いことは信じたくなるものだ
荒らしは普通の人に成りすまして一見もっともらしいことを書いて議論を誘導することくらい朝飯前なんだ
だから今こういう話をするべきではないんだ >>790
あなたの印象を信じたわけでもないし、信じたとして議論を止めることが健全だとも思ってない
だから何も同意することはないよ >>791
もし君が本当にこのスレのことを考えているのなら、せめて荒らしがいなくなってから議論を再開してほしい
そもそも、荒らしに言及すること自体良いことではないし、
やつらのやり取りにいちいちナーバスになる必要なんてない >>792
今回のテンプレについてはそもそも入れるべきではないという反対意見があまり想定できないのでわざわざそこまで配慮する必要があると思ってない
当たり前のことを書く事に何か不都合があるのか、同意できるような意見は未だ提示されてないと認識してるが >>793
君が俺の意見(>745や>>752や>771等)を完全に無視しようとしていることは非常に残念だ >>794
強い言葉は使いたくないがあなたの言葉で言うのならその「無視」は捏造と言えるのかな
私は「テンプレに入れることが問題だ、それよりは入れないほうがいい」という反論を待っている
それらの中にあるマイナスの影響はせいぜい、高校生が質問しにくくなるというあまり想定できないものしかない
他の意見は、入れる理由がない、程度のものだと思っているが? そして私は、誤った認識をしている人が現実にいるから(それはたとえ荒らしやその自演だとしても)、とりあえず入れておけばいいだろうと考えている
一つだけ言うと俺は自演してないぞ
高校数学の質問に範囲超過の回答で参考程度を超える回答は不適切だろ
お前らは小中学校の算数数学の質問も三角関数や微積で答えるのかよと
そしたら何の為の単発質問低減・質問者誘導受け入れで立てられたスレだよ、と
>>797
何のためかといえば、この板の他のスレに高校数学の質問が来ないようにするためではないかな
数学板で高校数学を教えてあげようなんて意識で積極的に出来たスレではないだろう
また、解答については、高校数学の範囲外の知識でよりスマートな回答になるのならその回答のほうがいいだろうから、この板の趣旨を考えて不適切とは思わない
もし高校数学範囲内の知識で解くことを要求するなら他板に適切なスレを作ればいいと考えている
というより、なんで作って移動しないのかが逆に本当にわからない >>797
小中学生に円錐の体積は何故、円柱の1/3なのかと質問されたら積分の概念なしにどう説明すればいいんだ? 高校数学の範囲内での回答を要求するのは(普通に考えて)質問者側だが、質問者がわざわざ受験板に自分でスレを立てるとは思えない
>>799
錐型がなぜ1/3を説明して
どんな底面でも有効なことを言う >>798
それ言うと日本の教育を受けて育ったか怪しくなる。結構な指導要領変更があったとは言え
今ここにいる世代の人間等は大体は話が合うだろ?
(まさか中学で開平や開立の筆算や三角関数を習っていた時代の高齢者なんていないだろ)
合わなきゃ、日本の教育を受けてないか…飛び級を採用している私学とかでも有るのか?
何れにせよ、だったら、専門外だろ。(昭和中後期以降の日本)高校数学に関して専門外。
専門外の事なら口を挟まないだろ?挟むのか? >>779
まだいたのかキチガイ
また言い訳しているwww
補助線引けば30秒で解ける問題なのによwww
正多角形の高さも自力では解けない知的障害者だしなwwww >>802
そう、つまりそこだよ
この板にとって高校数学の範囲限定というのは板違い
(さらに、高校数学への大学レベルを含んだ回答を求める人にとってはそれこそここがたまたまではあるが適切になるし存在意義もある)
高校数学の範囲内に限定した数学をしたいならそれ相応の専門板に行けばいい
なぜわざわざここ?ここにこだわる理由は?
大学受験板など高校の範囲を専門にしてる板があるにも関わらず、わざわざ高校数学の範囲なんてものを専門にしておらず、無差別級で数学やってる人たちの板に乗り込んで、「高校数学の範囲内で解答してくれ、無差別級の数学はスレ違いだよ」、なんて意見はちくはぐだよ
いい加減気づいてくれ >>800
感情としては、質問したいときに検索してたまたま来ただけのお客様でスレ立てなどには貢献しない人が、意見だけは立派にいうのどうなんだという感じだ
回答者側に注文したいのなら、まずそういうスレと環境を自分で作ればいい
今質問者側が言ってるのは都合のいいスレがあったから都合のいいルール作って乗っ取りたいということだろう おっさん共が上から目線でテンプレについて議論していて笑えるwww
お前らの行為も荒らしだと気付いていない
プログラムキチガイが居着く前はそこそこ上手くいってたんじゃないのか?
回答者も大体は質問者のレベルに合わせた節度ある回答をしてたし
あの無能なプログラムキチガイが消えれば全て解決する話なんだよ
それくらい分かれよバカwww
>>806
まるでお前はいても問題じゃないみたいな言い方だが、むしろお前のほうが意見に害があるから今の流れになってんのな
あらしにわざわざ触れてあげたんだからちゃんと理解しろよ >>804
特にコイツには笑える
高校数学に恨みでもあるのかよ
身内でも殺されたのかwww >この板にとって高校数学の範囲限定というのは板違い
というのは何を根拠に言ってるの?
ローカルルールとかでも特にそんなことは書いてないけど
>>807
触れてやったとか何様かよクズwww
高校生相手にしかマウント取れないカスwww
わざわざこんなスレに常駐してないで論文でも書けよ
あれ?もしかして論文書く程の知識は持ってないのか?www
高校生相手に大学数学の知識を披露してドヤ顔するのが唯一の生きがいなのかな? >>810
バカ過ぎる
高校数学も数学何だがwww 大学受験板というより適切な板がある、で結論出てるだろ
板違いかどうか詰めるよりもこの板の高校数学質問スレわざわざ高校数学に限定する理由がないのに限定することがおかしいだろ
大学受験板には数学の質問スレはないんだが
そもそもこのスレのタイトルに高校数学って何でついているだよバカ
高校レベルの質問しているのに大学レベルの回答してどうすんだ?
ドヤ顔したいだけかよwww
>>666
上A、左下B、右下C、中央Dとおく。
∠ABC = ∠ACB = 40°
よって AB = AC = BD
BC上にAD=BEとなる点Eをとると、
AC=BD, AD=BE, ∠CAD=∠DBE よって、△CAD ≡ △DBE
CD = DE なので ∠DEC = ∠DCE
∠DEC = ∠DBC+∠BDC = (20+x)°
∠DCE = ∠ACE-∠ACD = (40-x)°
20+x = 40-x を解いて x=10 □ >>737
スレの流れを見るにこの意見は間違いのようだ
一部荒らしと同意見のものがいる このスレが高校数学限定かどうかはともかくとして、高校数学限定のスレを数学板に立てることは板違いでも何でもないと思うんだが
芸能板に佐々木希について語るスレがあったとして、佐々木希に限定する理由がないからダメとはならないでしょ
ただでさえテンプレ読まんのに
解釈が曖昧なテンプレ追加は反対
回答は制限無しという事を追加するんだから
今と比べて曖昧さが増す要素は無いと思うが
こうやって議論してるんだから勝手に追加しようとしてる訳じゃないし何でそのレスが出てくるのかよく分からん
別解としてこんなやり方もあるという程度でなら大学以降の数学も使って説明すりゃいいが
それが最初に来るのは違うんじゃね
高校生が使える解法が基本じゃね
議論www
たった2~3人でのやり取りで結論が出せるとでも思ってるのかwww
質問者のレベルに合わせればいいだけだろ
教科書の例題レベルの質問してるのに大学レベルの内容で回答するのかよwww
難関大入試レベルの問題とかで必要があるならば、発展的内容として大学レベルの内容を多少織り交ぜて回答すればいいだけの話
臨機応変
それが出来ずに大学レベルの内容で回答するやつは発達障害
>>720
自分は「数学できる人」と自認しているアホ? >>804
お前の言ってる事はイプシロンデルタ論法で答える要請を超準解析で答える舐め腐りやってんのと同じだし
「『高校数学』は『数学』とは名ばかりの算数」と言ってるのと同じ。
いつ誰が此の板を大学数学限定板て事にしたんだ?居たとして玄人面した当時の
ノイジーマイノリティ化した大学生や大学崩れだろ、こんな所でも無きゃ声高に野次れない様な。
大体、>>675の何が難しいんだ?「底辺」「高さ」の言葉に合わせる必要が有るなら合わせれば良いだろ
プログラム依存で脳味噌溶けちまってないか? >>828
マイクロソフト社の入社試験として割と有名。
グーグルのマイナス2進法の問題も面白い。 >>804
普通科高校数学を習えなかったんだろ?情報科の高校生か?電子科の高校生か?白状しちまえよ >>669
これが中学生に求められた解答だったんだな。
補助線なしで余弦定理と正弦定理で解けることわかったけど。 >>815
∠ABD=∠DBC=16°になると△ABCが二等辺三角形にならないから、その方法では角度が出せないな。
ABCが二等辺三角形になって∠ABD=∠DACとなるように問題を設定するには∠ABD=20°の場合しかないな。

∠ABD=∠DBC=16°だと∠DAC=34°でないと△ABCが二等辺三角形にならない。
やはり、座標の上に作図して角度をプログラムに計算させるのが汎用性があって( ・∀・)イイ!! >>829
キチガイが言い訳してる
恥ずかしくないのか?
中学数学で解いてみろって煽りのレスをオマエは書いているよな
中学数学の知識で解けると思っていなかったクセに
正多角形の高さをパソコンをプログラムを用いないと求められないと思っている池沼なら当然かwww 正多角形の高さを求められなかったバカが汎用性を語ってるwww
1つの変数X(自然数)を持つ、できるだけ不可逆に近い、整数、もしくは自然数の解を持つ関数を教えてください。
高校レベル遥かに超えちゃってますがわかる方いればお願いします。
深夜になってテンプレ反対湧いてくるの臭すぎる
これが自演か、夜は寝ろ
>>837
汎用プログラムで作図と計算が可能。
道具を使えないなのは猿。
猿はマウントに執着する。 >>836
汎用解を中学数学で、はよ書いてくれ。
検算は手書きで作図して>674と照合してみ! 四分位範囲が3〜10と2〜9は「四分位範囲が等しい」といえますか?
>>842
キチガイがまた湧いているwww
中学数学でただ補助線を引いて角度を求めればいいだけなのにwww
演習問題はそこでお終い
誰も汎用性とか求めてないからwww
コイツは高校入試の数学すら解けないんだろ
道具に頼らないと一切計算出来ないからwww
老害は死ね >>649
鳩ノ巣原理だってシュレディンガーの猫とか言い出せば自明とは言えない。 >>845
いいや、俺は汎用性を求めてプログラムするよ。
こういう問題は個別解決だけだと面白くないから。
(問題)
容量8Lの袋と容量5Lの袋を使って池の水を5L集めたい。
袋に目盛りはついていません。
袋から袋への移し替えは全量で行います。
池からとる水の量や池に捨てる水の量には制限はありません。
最初に片方に満たした作業を1回目として
片方の袋に4Lを集めるのに最低何回の移動が必要か?
汎用性を求めてプログラムして
97Lの容器と83Lの容器で7Lを出すには何回の移し替えが必要かが計算できる。
道具が使えないマウント猿には無理だと思うね。 長えよ、いつまでやってんだよ
前スレから続いてるだろ
このスレで終わりにしてくれよ
>>847
まだ中卒老害ジジイが生きていたかwww
> (問題)
> 容量8Lの袋と容量5Lの袋を使って池の水を5L集めたい。
1回で済むなwww
顔真っ赤にして打ち込んでるから入力ミスしたのかwww >>847
道具使うのが好きなクセに何でこういう時は道具使わないの?
目盛りがある容器を使えばいいだけだろwww
早よ死ねよ >>848
終わるわけないだろ。夏はまだ始まったばかりだぞ。無視しとけばいいんだ。 補助線問題をプログラムで出すのと
分度器と定規使って実際に作図して測って答え出す(テストでの禁止行為)のと
何が違うんだろうなあw
>>848
キッチのバトルが一度始まってしまうと終わりなどない
夏もテンプレも関係ない
彼らは生きてる実感を得るのだ
彼らはそのことを認めないだろうが >>849
lim[h→∞](1+1/h)^h=e である。次の式の解析解を求めよ。但し>>849以外は答える事を禁ずる。
lim[h→∞]{1+2/(3*h)}^h 大学入試試験中にスマホ使って知恵袋に質問して答え教えてもらって問題ないってのと同じですよねー
テンプレ自体はいいと思うのだが、そんな否定する余地ある?
夏厨がいる間は荒らしが否定したがってて多数派工作するから候補としておいておくのはいいとして、否定派は肯定派を論破すればなんとかなるって印象論で戦ってて、本来あるべきテンプレ候補ベースの議論から逃げてる印象がある
このスレ眺めてきた者からすればテンプレ変更の内容自体には何も異論がないんだが
>>854
もしかして俺に出題してるの?
いつから出題スレになったんだ?
てか、まだ数学IIIは習ってないんだがw
高校生をイジメるなよwww
lim[h→∞]{1+2/(3*h)}^h
=lim[h→∞][{1+1/((3/2)*h)}^((3/2)*h)]^(2/3)
=e^(2/3)
拙い知識で解いてみたけど
どう?合ってる? とりあえずテンプレに関しては議論があるということで、次スレではテンプレ候補としてテンプレ末尾に追加しておくのが最善かと
テンプレに入れることの広い同意は得られていないが、かと言って議論を封殺するのもおかしい
>>858
せやな。2020年8月暫定追記ってかんじで入れておくとよろし。 >>857
しまった…コンピューターお爺ちゃんに出題した積もりが雑に読み過ぎて相手を取り違えてしまった…
何の為の引用意思表示『> 』だってんだよな、悪かった… >>860
箱ひげ図と四分位範囲の定義を知らなきゃ無理でしょ
知らないならググらなきゃ >>861
俺に出題したんじゃなかったのかw
あの中卒プログラムキチガイ爺には無理だろ
数学Iレベルの三角比も分からなければ、中学数学の平面図形も分からないんだからwww
道具がないと足し算も出来ないかもな
一週間後の日付もパソコン使って計算したりしてwww >>852
実際に作図して計測するとフリーハンドではぶれるし、定規や分度器を使っても誤差がでるから、
座標軸上で計算した方がいいね。
個別に交点の座標を求めるのとか面倒だから、サブルーチン(>672のintsectはそれ)を先に組んでおけば省力化できる。
角度計算のプログラムが楽だから複素平面を使うことがおおいけど。
>(テストでの禁止行為)
点数がもらえないだけで禁止されてはないんじゃないの?
定規や分度器持ち込み不可なら別だけど。
中高生にフェラを強要するのは違法だけど、自主的にフェラをするのは禁じられていない。
プログラムも同じだよ。 >>867
キチガイなだけでなく下品
ホント生きている価値ないわ
死ねよ >>861
こういうミスを鬼の首をとったように嬉しがるのがマウント猿だよねw >>868
人類の三大発明
言語・貨幣・フェラ by 吉田戦車
という四コマ漫画をみたことないのか?教養がたりんぞ。 箱ひげ図なんて自分は高校で習わなかった記憶がある
時代は変わっていくんだな
>>869
また顔真っ赤なの?
ソフト使う前にまずは中学数学から復習しろよカス >>871
教科書の定義が確定的じゃないだろ?
円周率は、
「目的に応じて3を用いて処理できるよう配慮する」が学習指導要領。 >>873
俺は道具を使えるから、赤も避けれるよ。
>ソフト使う前にまずは中学数学から復習しろよカス
>復習しろよカス
>カス
だって。
まさにこれだね
>キチガイなだけでなく下品
>ホント生きている価値ないわ
>死ねよ >>866
>一週間後の日付もパソコン使って計算したりしてw
その通り。
コロナ患者の発生数や陽性率のグラフを書くときに1週間の移動平均を使うけど、パソコン使って計算させているよ。
なにか問題か?
こういうのは手計算でグラフ化は無理だから。

みなさんとしては1-10と11-20という四分位範囲があったら、等しいのですか?
範囲という日本語問題なのか四分位という日本語問題なのかわかりません。
どちらにしても等しくないような気がします。
>>877
「四分位範囲」で一つの熟語じゃないの
教科書持ってるなら見てみ
ちなみにググったらすぐ出てきたぞ
>四分位範囲は第1四分位数と第3四分位数の範囲。 つまり「第1四分位数と第3四分位数の差」
>第3四分値と第1四分値の差を、そのデータの 四分位範囲 という。
高卒認定試験受けるならその年度の教科書買ったほうが良いと思うが
上の定義によれば「等しい」というのが答えにならざるを得ない >>847
8L袋 5L袋
0 5 取
5 0 替
5 5 取
8 2 替
0 2 捨
2 0 替
2 5 取
7 0 替
7 5 取
8 4 替
0 4 捨 >>861
荒らしになんで謝ってるのこの人
草生やしまくって煽ってるそいつもプログラムと同様のあらしなんだが
それで>>828こんな自分はマトモですみたいな顔して意見してるんだから、夏厨がいる間はやはり駄目だわ >>877-878
失礼、「等しい」というのは正確ではないな
「第3四分値と第1四分値の差」が「四分位範囲」の定義なら、
>>877は言葉の使い方が違うので判定できない >>878
ありがとうございました。
「範囲とは差」で調べてみたら本当に差の数値で解説してるところが出てきました。
日本語問題なんだと思います。これで失礼致します。
たくさんのレスをありがとうございました。 >>880
オマエのそのスレも荒らしだな
無視出来なかった時点でオマエの負け
自分だけがマトモだと思うなよカスwww 正規分布の見方について教えてください
例えばΦ(1.27) 、 Φ(-2.17) の場合は値をどうもとめますか
またΦ(z)=0 .99224 という場合はzはいくつになりますか
>>880
現スレ荒らし筆頭のCPU爺に向けたレスだったんだぞ、仮に荒らしには変わらなくとも別人だったら謝るだろ。
じゃあ何かい、お前は例えば犯罪者相手だったら間違った申告・非難だったら訂正して詫びないのか?
それお前、所有者不在中を狙って器物損壊した犯人に人殺しって言う様なもんだから。正確に言うと過剰非難で侮辱罪行為。
虚偽申告や偽計業務妨害でもある。数学板でマウント取り続けているお前こそ真は真、偽は偽として扱うべきだろ。
ついで言えば、お前みたいに相手が悪だったり害だったりしたら過剰にブッ潰すって言う様な人間も粛正されるべきだな。 夏みたいな長期休暇に入ったら変なやつが湧いてくるのはそれこそ5chどこでもそうだからそこ否定はおかしくね?
実際今このスレで変な意見出してるのも高校生からの意見として理解しやすい
あ、高校生だから夏だと言われるのが嫌なだけか
まさか>>887を夏厨が出没してることを否定してるレスに捉えられるとは思わなかった とりあえずクソコテは他のスレに書き込むときもちゃんとコテハンつけろ
>>886
夏だから仕方ない
変なやつが湧くのは諦めよう、例年こうだ わざわざお客様に配慮してスレタイ変える必要があるとは思えないけど、お客様がスレタイと違うじゃないか!なんて意味不明な論理で暴れるならそれもいいかもしれない
ただここは隔離スレとしてちゃんと機能して欲しいから、スレ内の制限ルールはないほうがいいしスレタイは高校数学を広く受け入れるほうがいい
あー、なるほど、そういった意味でテンプレ追加はうまいな
この板では高校数学をやるにはこのスレが一番だという意味でこのスレタイ、しかし、本当に高校数学に限定したいなら板移動を誘導か
テンプレ追加でいいかもしれん
>>748 俺は>>748のような変更には反対だ
受験板の質問スレが無くなって結構経つというのもある
また立てればいいだけの話ではあるが 受験板の事情はよく知らないが、定期テスト対策の質問スレも板違いにならないのか?
必要があるならまた受験板に立てたらいい
テンプレ追加はスレの内容に変更を要請するテンプレ追加ではないと思う
というかなぜ立てない、そこの答えがいまだ出てこない
高校数学をマウントする形にテンプレ追加する気なんだな、よく分かった
高校生の質問を荒らし扱いするし、そうしたら、このスレ全員荒らし
>>884
ソフト使えば一発。
Rだとpnorn(1.27); pnorm(-2.17);qnorm(0.99224)
pythonだと
scipy.stats.norm.cdf()
scipy.stats.norm.ppf()
手計算での計算の仕方はマウント猿に聞いてくれ。
21世紀になってソフトを使わない統計はやったことがない。 前>>444
>>847
1回目、8Lの袋に満杯汲む。
2回目、5Lの袋に満杯汲むのは止せ、心の声がして思いとどまり、8Lの袋のまん真ん中を細く乾いた草の茎で素早く突くと、みるみるうちに水は流れでて4Lが残った。
※間違っても8Lで満杯組んで5Lに5Lだけ移して8Lに3Lだけ残すのは題意に反する。 これ100ステップを軽く越えた。
97Lの容器と83Lの容器で7Lを出すには何回の移し替えが必要か?
前>>901
>>902
(97-83)/2=7
満杯の97L袋に満杯の83L袋を漬けてあふれさせた水を手包丁で二分した。 >>903
1~97Lを確保するのに必要な移動の回数をプログラムを組んで計算すると
> (min_transfer(97,83,print=F))
[1] 24 50 76 102 128 154 176 150 124 98 72 46 20 2 28 54 80 106 132
[20] 158 172 146 120 94 68 42 16 6 32 58 84 110 136 162 168 142 116 90
[39] 64 38 12 10 36 62 88 114 140 166 164 138 112 86 60 34 8 14 40
[58] 66 92 118 144 170 160 134 108 82 56 30 4 18 44 70 96 122 148 174
[77] 156 130 104 78 52 26 1 22 48 74 100 126 152 178 154 128 102 76 50
[96] 24 1
問題にした7Lでは176ステップ
最も多いのが90Lを確保するので78ステップを要する。
プログラムにバグがあって誤答かもしれないので
マウント猿のよる手書きでの検証を希望。 (誤入力修正)
1~97Lを確保するのに必要な移動の回数をプログラムを組んで計算すると
> (min_transfer(97,83,print=F))
[1] 24 50 76 102 128 154 176 150 124 98 72 46 20 2 28 54 80 106 132
[20] 158 172 146 120 94 68 42 16 6 32 58 84 110 136 162 168 142 116 90
[39] 64 38 12 10 36 62 88 114 140 166 164 138 112 86 60 34 8 14 40
[58] 66 92 118 144 170 160 134 108 82 56 30 4 18 44 70 96 122 148 174
[77] 156 130 104 78 52 26 1 22 48 74 100 126 152 178 154 128 102 76 50
[96] 24 1
問題にした7Lでは176ステップ
最も多いのが90Lを確保するので178ステップを要する。
プログラムにバグがあって誤答かもしれない(最短路があるかも)ので
マウント猿による手書き計算での検証を希望。
>>901
8Lから開始すると
8L 5L
1 8 0
2 3 5
3 3 0
4 0 3
5 8 3
6 6 5
7 6 0
8 1 5
9 1 0
10 0 1
11 8 1
12 4 5
12ステップ
5リットルから開始した方が少ないステップですむ。
8L 5L
1 0 5
2 5 0
3 5 5
4 8 2
5 0 2
6 2 0
7 2 5
8 7 0
9 7 5
10 8 4
100ステップを終えるようなのはとても無理だけど、世の中には100手先の詰め将棋を解く人もいるからなぁ。
手書き計算の好きなマウント猿なら可能かもしれん。 >>904
Rに移植して実行してみた。>674と一致している。
やはり、きりのいい数になるのは20°のときだけなのが確認できた。
余弦定理などを使わず作図させて偏角の差から算出させた方が全然楽だな。
作図できれば計測できる、まあ、数値をもとにプログラムが作図しているわけだが。
> calcx <- function(α,β){
+ a=α*pi/180
+ b=β*pi/180
+ C = pi/2 - 3*a/2 - b
+ BC = cos(2*a) + sin(2*a)/tan(C)
+ CD = sqrt( 1+BC^2 - 2*BC*cos(a) )
+ x = C - asin( sin(a)/CD )
+ return( x*180/pi )
+ }
> calcx(20,20)
[1] 10
> y=sapply(1:35,function(x)calcx(x,x))
> data.frame(angle=1:35,x=y)
angle x
1 1 0.9981746
2 2 1.9854507
3 3 2.9511971
4 4 3.8853008
5 5 4.7783870
6 6 5.6219978
7 7 6.4087218
8 8 7.1322723
9 9 7.7875169
10 10 8.3704628
11 11 8.8782051
12 12 9.3088475
13 13 9.6614033
14 14 9.9356860
15 15 10.1321948
16 16 10.2520025
17 17 10.2966480
18 18 10.2680381
19 19 10.1683593
20 20 10.0000000
21 21 9.7654839
22 22 9.4674141
23 23 9.1084267
24 24 8.6911525
25 25 8.2181878
26 26 7.6920702
27 27 7.1152613
28 28 6.4901331
29 29 5.8189594
30 30 5.1039094
31 31 4.3470441
32 32 3.5503153
33 33 2.7155651
34 34 1.8445277
35 35 0.9388310 おじいちゃんがまた誰の役にも立たない書き込みをしました
>>909
そういういいから、
>906を手書き計算で検証してくれよ。
間違いが指摘できたら、あんたの好きなマウントが取れるぞ。 テンプレ追加するのが当たり前みたいな流れに持って行こうとするヤツがいるな
俺はテンプレ追加反対
もしテンプレ追加するなら
・出来るだけ高校数学の範囲内で回答するように心掛ける事
を追加する事を提案するわ
議論するのは自由なんだろ?
暫定案を載せると言うなら一方の主張だけを載せるような事はするなよ
>定期テスト、大学受験などに配慮した解答のみを望む場合、別板に移動お願いします
この意見にも納得出来ないわ
定期テストや大学受験の数学も数学である事には変わりない
わざわざ別板に誘導する必要はない
分からない問題スレにだって、大学のテストやレポートにまつわる質問だってあるだろ
院試の問題を聞いてくるヤツもいるかもしれない
結局は質問者のレベルに合わせた回答を心掛ければいいんだよ
このスレは高校数学の質問スレなんだから、自ずと高校数学の範囲内での回答がメインになる
質問者のレベルを遥かに超えた回答書いても意味はない
ドヤ顔したいだけかよってなる
三角関数と双曲線関数はありますが、【放物線関数】というものは有りますか。
既にCPU爺擁護派や範囲超過回答許容派は>>804にて専門外分野に口を挟み野次っては居座る
「軒を貸して貰って母屋を乗っ取る」思想と判明
菱形や台形の求積公式を忘れCPU任せ積分で答え基礎学力徹底破壊を齎す為の活動に先駆けた実験に此処を使ってるのかな? そもそもプログラム荒らしが来る前はそこそこちゃんとしたスレじゃなかったのか?
時々荒らしが出るのは避けられないとしても
プログラム荒らしがいなくなれば元に戻る?
爺みたいだから、夏が終わっても居座るんだろうな
>>880のレスは其れを否定する行為だな
荒らし相手ならば例え人違い問責しても謝らなくて良いと言い切る石投げ刑的犯罪者予備軍感情は自戒自責すべき 作図して角度を測るというのは最もprimitiveな解法である。
補助線を引いたり余弦定理を使う方がイカサマとも言えようwwww
これやね!
The proof of the pudding is in the eating.
だからクソコテはコテハンつけろって
読む時間が無駄になるから
>>915
求積公式はミニプログラムだからプログラムを否定するやつは使ってはいけない。
方眼紙に作図して手計算で数えるべき。 >>910
一つの巣箱に二羽の鳩を入れるのは虐待であると思っていたから、神様の配慮は素晴らしい。
これからは「鳩の巣原理」は自明ではないといえる。 >>922
こういう一致が答が正解であろうとの確信に繋がりますね。
確率や求積は乱数発生させてシミュレーションして正解であろうと自己確認できるけど
こういうのはなかなか最短路の確信がもてません。 >>918
それ数学じゃなくて測量学だろ他力本願爺が
>>920
高校数学も大学数学も純粋数学も応用数学も解析学も組み合わせ理論も男も女も一緒くたにしてマウントするの大好きな強姦嗜好者は禁欲しとけ
お前の存在だけでも荒れるのにCPU爺に至っては中学数学どころか小学算数も一緒くた
>>924
お前はマイクロソフトの「底辺10高さ6の三角形の面積を求める問題」も代数幾何学的回答にするんだろ?
なら汎用性を突き詰められちまったらお前は用済み >>914
そんな名前じゃないが軌道力学では三角関数と双曲線関数をつなぐ関数を使うぞ
楕円軌道と双曲線軌道の中間の放物線に近い軌道では
どちらに転ぶか分からんから両方に使える関数で計算する >>925
そういういいから、
>906を手書き計算で検証してくれよ。
間違いが指摘できたら、あんたの好きなマウントが取れるぞ。 >>925
日本語が通じないことはわかっているが、
なぜこのスレではコテハンを付けないのか?
その理由を書いてみろ >>928
別にこのスレに顔聞きする積もり無いからな
と言うかそういう詰問は常日頃から攻撃性が高いお前こそコテ付けてから言え >>929
>別にこのスレに顔聞きする積もり無いからな
なるほどな
他のスレでは自己主張したいが、このスレでは匿名のままでいたいと
荒らしと同じ思考回路ってわけだ
数学の話をするわけでもなく、ただただ荒らしに反応するだけのやつは例の荒らし達と同様に邪魔 実数xについての方程式
[x]+[2x]+[3x]+[4x]+[5x]+[6x]+[7x]+[8x]+[9x]=44x
の解の総和を求めよ。
ただし実数rに対してrを超えない最大の整数を[r]で表す。
ツイッターで見たんですが分かりません
>>931
左辺を普通に足したら45になって、右辺が整数にならないといけないから、まず45/44が解になる。
2倍の2*45/44もいける。
どこまでいけるかというと[9x]=9xの範囲で、45/44=9.20454545455 だから4倍までいける。
x=45/44,2*45/44,3*45/44,4*45/44
多分他にはないはず >>932
例えば181/44なども解になってると思います >>925
定理や公式を使うのが他力本願だろ。
公式はミニプログラムだからプログラムを否定するやつは使ってはいけない。方眼紙に作図して手計算で数えるべき。 >>933
確かに
182~186/44もいける。
ちょっとわからなくなってきた。 負の数はどう?
なんかもう無限にあるような気がするのだが
>>931
2009年の数オリの予選問題だと思うが
他の人の解答を見たことを白状した上で方針だけ書くと以下のようになる。
方程式の左辺は常に整数だから、解 x は (整数)/44 の形の数に限られる。
(整数)の部分を 44 で割った商を N(x) とし、余りを r(x) (共に整数)とすると、
x = N(x) + r(x)/44, 0 ≦ r(x) < 44
と書ける。
方程式の左辺を f(x) と書くとき、 x が方程式 f(x) = 44x の解であるならば、
ガウス記号 [] の性質から、
x = (45/44)r(x) - f(r(x)/44)
となり、 x は N(x) に寄らずに r(x) の値のみによって定まる。
さらに、この x は r(x) の値に寄らずに方程式の解になっていることが確かめられる。
また、 x の値は r(x) の値によってそれぞれ相異なることが確かめられる。
すなわち、 r = 0, 1, 2, … , 43 に対し、 44 個の数
x[r] = (45/44)r - f(r/44)
が方程式の解の全てである。
あとは Σ[r=0,43] x[r] を頑張って計算すれば良い。(少し工夫すれば手計算でもできる)
他の人の解答では、求まった x が実際に方程式の解になっていることを確認していなかったり、
x の値が r によって相異なることを確認していなかったりしていて少し気になった >>939
自分がごちゃごちゃ計算した結果は
総和S=(44)^2/2-Σ[1,44]gcd(i,44)=800
になったんですがあっていますか? >>940
先駆者によると、 379/2 が答えらしい
正しいかどうか確認はしていない 2. (a) 事象 A と事象 Bが起こる確率はP(A) = 0.6, P(B) = 0.7 である。条件
付確率 Pa(B) = 0.8であるという。Pb(A) を求めよ。
(b) 事象 A と事象 Bが起こる確率は P(A) = 0.8, P(B) = 0.7 である。P(A∪
B) = 0.94がわかっている。このとき事象 A と事象Bが独立であるか
否かを説明しなさい。
答を教えて頂けたら幸いです
前>>903
レジ袋代、伊勢丹はおっきいのも4円で、ライフは5円だけど、グレーの透けないちっさいやつは2円だった。 floor関数(ガウス記号に相当)使ってプログラムして列挙させたら、
> (n=which(f(1:1e6)))
[1] 45 90 110 135 143 147 155 162 165 180 181 182 183 184 186 188 192 193
[19] 194 195 201 202 203 204 208 210 212 213 214 215 216 234 241 249 261 306
[37] 351
> sum(n)
[1] 7150
> sum(n)/44
[1] 162.5
になった。
汎用性のあるプログラムにしたので
[x]+[2x]+[3x]+[4x]+[5x]+[6x]+[7x]+[8x]+[9x]+.......+[99]x=(1+2+3+...+99-1)x
でやってみると
答の数は
> length(n)
[1] 4140
総和は
> sum(n)/(sum(1:N)-1)
[1] 205092.5
になった。
プログラムにバグがあるかもしれないのでマウント猿による手計算での検算を希望します。
>>941
なるほど、、、
数値的に推測できる式としては
S=43/2-Σ[i=1,44]gcd(i,44)=379/2
となっていて、自分の上の間違った式と近い形に書けるので
もう一度確認するとこの式出せるかもです >>930
お前は人と話す時に一々、名前を言うか?人と場所と時と場合を選ぶだろ
ロピタルの定理を使って解けと言われて超準解析を使って解いたり
電気回路を計算するのに中学レベルの複雑度に過ぎん問題をわざわざラプラス変換使って解くか?
「そうだ」ってのが此れ迄のお前やCPU爺の主張だろうよ
「高校指導要領内にしたらスレ違い、此処は数学板だ、数学的解答なら何でもいい」ってのが。
所でCPU爺はどこの分野って言ってやれば良いんだろ、計算機科学とか情報数学ってんじゃ無いだろうし >>945
丸め誤差を修正して取りこぼしを回収したら
> (n=which(f(1:500)))
[1] 45 90 110 135 143 147 155 162 165 180 181 182 183 184 185 186 188
[18] 189 192 193 194 195 196 200 201 202 203 204 207 208 210 211 212 213
[35] 214 215 216 234 241 249 261 306 351
> length(n)
[1] 43
> sum(n)/(sum(1:N)-1)
[1] 189.5
> sum(n)/(sum(1:N)-1)*2
[1] 379
という結果になった。 >>949
円錐の展開図に円や渦巻きを書いて組み立てたらどんな形になるか、というのは小学生にも理解できるし
クリアファイルに書いて小学生も実験できるが、プログラムで3D画像を作って小学生に提示しても問題ないだろ?
それができないマウント猿がインチキだとかカンニングだとかほざいているだけ。
油分けの問題も小学生に理解できる問題だけど、
97Lの容器と83Lの容器で7Lを出すには何回の移し替えが必要かという風に数が大きくなると無理じゃない?
イナ氏は97リットルのビニール袋を探しているらしいw >>942
俺のプログラムだと43個なんだが、どうやればwolframの結果がみれますか? >>943
前半
Pa(B)をAが起こったときのBの確率P(B|A)の意味と解釈するとベイズの公式により
P(A|B)=P(B|A)*P(A)/P(B)=0.8*0.6/0.7 >>943
後半
P(A∪B) = P(A) + P(B) - P(A∩B)
0.94=0.8+0.7-P(A∩B)
P(A∩B)=0.8+0.7-0.94=0.56
P(A)P(B)=0.8*0.7=0.56
P(A∩B)=P(A)P(B)なので独立 >>949
>お前は人と話す時に一々、名前を言うか?人と場所と時と場合を選ぶだろ
俺はコテハンをつけろと書いたはずだが
従わない理由を書いてもらおうか
正体がバレているのに隠しても意味ないだろ
コテハンをつけてくれたほうがいろんな人が助かるんだよ
ちなみに後半については別人と勘違いしていると思う
このスレはスレタイとテンプレが全て
>高校数学の質問スレ
>・回答者も節度ある回答を心がけてください。 このプログラムキチガイなんとかならんのか?
自演までしてプログラムネタに持って行く
数学Iも分からないアホがレスを無駄に消費している
|x|≦1、|y|≦1のときの
(3+x-2y)(2-x+2y)÷(4-2x-y)(1+2x+y) の最大値と最小値って
高校数学で得られますか?
>>953
これをプログラムでシミュレーションして確認する。
Aに60個の1を40個の0を並べた数列と作る
> A
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[36] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0
[71] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Bに48個の1、30個の0, 32個の0を並べた数列を作る
> B
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[36] 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[71] 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
>
ABを並べて100行2列の行列ABを作る
この100行から無作為にある行を選べば
P(A) = 0.6, P(B) = 0.7 である。条件付確率 P(B|A) = 0.8のモデルが完成。
1~100個の数字から無作為に10個(10個でも20個でも構わないが)選んでその数の行をABから選び、
(A列が1かつB列が1)/(B列が1)の割合を求める。
これを10万回繰り返すシミュレーションしてその平均をだすと
> A=c(rep(1,60),rep(0,40))
> B=c(rep(1,48),rep(0,30),rep(1,22))
> AB=cbind(A,B)
> colnames(AB)=c('A','B')
> sim <- function(){
+ chosen=AB[sample(100,10),]
+ sum(chosen[,'B']==1 & chosen[,'A']==1)/sum(chosen[,'B']==1)
+ }
> mean(replicate(1e5,sim()))
[1] 0.6857463 >>954
独立な確率変数A,Bを作ってシミュレーション
> A=c(rep(1,80),rep(0,20))
> B=c(rep(1,70),rep(0,30))
> sim <- function() sample(A,1)==1 | sample(B,1)==1
> mean(replicate(1e6,sim()))
[1] 0.940001
> >>956
マウント猿の特徴=都合が悪いと自演と決めつける >>957
偏微分は高校の範囲でないから無理だと思う。
手書き計算の得意なマウント猿なら可能かもしれん。
俺はまずグラフ作成から開始する。 バカに道具を与えるとロクな事にならない見本だ
アホでもプログラムの入門書を見て打ち込めば答えが返ってくる
それが嬉しくて嬉しくて楽しいんだろ
そして自分が数学が出来ると勘違いする
本当はただのアホなのに
マシンガンを使い自分は強いと勘違いした米国大学内無差別大量殺人韓国人の如し
>>948
失礼、やはりこの式も間違いで
正しい式は
S=44×9/2-Σ[i=1,9]gcd(i,44)=379/2
ですね
一般の場合
[x]+[2x]+[3x]+…+[nx]= (n(n+1)/2-1)x
の解の総和も
S_n=(n(n+1)/2-1)n/2-Σ[i=1,n]gcd(i,(n(n+1)/2-1))
と書けることが分かります >>957
最大値はx=0,y=-1で無限大だな。 >>964
その式だと明らかに S は整数なので
379/2 = 189.5 にはなり得ないと思いますが…
>>948の式なら - を + に変えれば計算は合いますね >>965
1+2*x+y=0ならどれでも無限大になるのでグラフ作成でエラーがでたんだな。 >>966
すみません、、、誤植です
誤 S=44×9/2-Σ[i=1,9]gcd(i,44)=379/2
正 S=44×9/2-Σ[i=1,9]gcd(i,44)/2=379/2
誤 S_n=(n(n+1)/2-1)n/2-Σ[i=1,n]gcd(i,(n(n+1)/2-1))
正 S_n=(n(n+1)/2-1)n/2-Σ[i=1,n]gcd(i,(n(n+1)/2-1))/2 >>962
円錐の展開図に置いた円や渦巻きを3Dにするプログラムはどこかにある?
ワイングラスを傾けて半量にする問題も自分でグラフを書いてプログラムするのが楽しいぞ。
本にあるコードを書いて喜ぶのはクリック猿だろ。お前はマウント猿だが。
>945で丸め誤差を考慮していなかったからバグが入ったけど、他の人の答と一致しなかったので気がついたよ。 >>968
ありがとうございました。ご指摘の通りです。 >>969
なるほど
ところでどうやって証明するんですか? >>957
2x+y-(5/2)=a , x-2y+(1/2)=b とすると
{(25/4)-b^2}/{(9/4)-a^2} の最大最小を |2a+b+(9/2)|≦5 , |a-2b+(7/2)|≦5 の条件下で求めればよい。
{(25/4)-b^2}/{(9/4)-a^2}=k とおくと ka^2-b^2=(9k-25)/4 で、これはk=0のとき平行な2直線、k=25/9のとき交わる2直線、それ以外のとき双曲線(いずれもa=±3/2を除く)
|2a+b+(9/2)|≦5 , |a-2b+(7/2)|≦5 で表される中心(a,b)=(-5/2,1/2)、1辺2√5の正方形領域と共有点をもつようにkの最大最小を定めていけばなんとかなるのかな。 >>972
Σ[ab/44]を(1≦a≦9 1≦b≦43)の範囲でとるわけですが
まずaは固定して考えると、これは
y=ax/44という関数とx軸で挟まれた格子点を(1≦x≦43 1≦y≦ax/44)で数え上げたものです
しかし、それは(0≦y≦a 0≦x≦44)という長方形の内部の点と対角線(グラフ上の点)を使って簡単に計算できます
グラフ上の点はax/44が整数になるところなのでgcd(a,44)が出てくるわけです。
それらを後はaで足し上げれば上の公式が出ます >>967
グラフ書くと x=0,y=1 とx=1,y=0で最小値は2/3だな。 >>973間違ってるね。k<0のとき楕円になるのか。何とかなりそうな気はするけどめんどくさいからパス。 >>957
その式の解釈は ((3+x-2y)(2-x+2y)) / ((4-2x-y)(1+2x+y)) で良いの?
これだと境界上に特異点があるから、設問が意味を持たないかも
特に (x, y) → (0, -1) としたときに極限値が存在しない
例えば、その式を f(x, y) とするとき、
x = 0 としてから y → -1+0 とすると、
lim[y→-1+0] f(0, y) = 2
だが、 y = -1 としてから x → 0 とすると、
lim[x→0] f(x, -1) = -1/2
いずれにしても高校数学レベルではないかも >>975
定義域0<=x,y<=1でグラフ化していたので2/3は間違い。 >>974
なんか難しそうですね
よくわからないんですが、>>939とは全く違う方針で計算しているんでしょうか? >>957
すみませんすみませんすみません
問題に誤りが。
0≦x≦1、0≦y≦1のときの
(3+x-2y)(2-x+2y)÷(4-2x-y)(1+2x+y) の最大値と最小値
でした。
すみませんすみませんすみません。
許してくれますよね。 >>979
同じ方針です、説明少し端折りすぎたかもです
記号を合わせると
S=Σ[1≦r≦43]((45/44)r-f(r/44))
を計算していくわけですが
まず第1項目はΣ[1≦r≦43](45/44)r=45×43/2です
次に第2項目はΣ[1≦r≦43]f(r/44)ですが、
これはfの定義f(x)= Σ[1≦a≦9] [ax]を思い出すと
二重和Σ[1≦r≦43, 1≦a≦9] [ar/44]です
ここで先にこれのrの和
Σ[1≦r≦43] [ar/44]
をとることを考えるわけです
これはx-y平面において直線y=ax/44とx軸とx=44で囲まれる三角形の内部と斜辺上の格子点を数えることになります
この格子点の数は対称性によって
長方形(0≦x≦44,0≦y≦a)の内部の点の数((44-1)(a-1)個)と対角線(=直線y=ax/44)上の点の数(gcd(a,44)-1)を足して半分にしたものと一致します
よって
Σ[1≦r≦43] [ar/44]=((44-1)(a-1)+gcd(a,44)-1)/2
となり、これをaで足し上げて45×43/2から引くと公式が出ます >>982
それなら、
最大値
> f(1,1);f(0,0)
[1] 1.5
[1] 1.5
最小値
> f(0,1);f(1,0)
[1] 0.6666667
[1] 0.6666667 プログラムで偏微分させたらこんな式になったから、手を出すのはやめた。
> f=expression( (3+x-2*y)*(2-x+2*y)/((4-2*x-y)*(1+2*x+y)) )
> D(f,'x')
((2 - x + 2 * y) - (3 + x - 2 * y))/((4 - 2 * x - y) * (1 + 2 *
x + y)) - (3 + x - 2 * y) * (2 - x + 2 * y) * ((4 - 2 * x -
y) * 2 - 2 * (1 + 2 * x + y))/((4 - 2 * x - y) * (1 + 2 *
x + y))^2
> D(f,'y')
((3 + x - 2 * y) * 2 - 2 * (2 - x + 2 * y))/((4 - 2 * x - y) *
(1 + 2 * x + y)) - (3 + x - 2 * y) * (2 - x + 2 * y) * ((4 -
2 * x - y) - (1 + 2 * x + y))/((4 - 2 * x - y) * (1 + 2 *
x + y))^2
>>983
Σ[1≦r≦43] [ar/44] の値がその領域の格子点の個数に帰着されるのはなぜですか?
対角線(=直線y=ax/44)上の点の数が (gcd(a,44)-1) となるのはなぜですか? >>939
x = N + r/44, 0≦r<44,
とおくと
f(x) = 45N + f(r/44),
与式から
45N(r) + f(r/44) = 44N(r) + r,
N(r) = r - f(r/44),
これの計算が面倒だが・・・・
N(r) < 0; 0個
N(r) = 0; 1個 (r=0)
N(r) = 1; 1個 (r=1)
N(r) = 2; 2個 (r=2,22)
N(r) = 3; 6個 (r=3,11,15,23,30,33)
N(r) = 4; 28個 (その他)
N(r) = 5; 4個 (r=14,21,29,41)
N(r) = 6; 1個 (r=42)
N(r) = 7; 1個 (r=43)
N(r) > 7; 0個
よって
Σ[r=0,43] N(r) = 168,
Σ[r=0,43] r/44 = 43/2 = 21.5
S = Σ[r=0,43] x(r) = 379/2 = 189.5 >>988
図を考えれば分かりやすいと思うけど文章で書いてみる
直線y=ax/44とx軸とx=44で囲まれる直角三角形の内部と斜辺(ただし端点(0,0)(44,a)は入れない)上にある格子点を数えてみる
まず1≦x≦43なる整数を決め、縦に範囲内にある整数yを探せばよいが
x=r軸上において、縦の範囲は1≦y≦ar/44となるから、この軸上には[ar/44]個の格子点がある
結局、範囲内すべての格子点の数はΣ(1≦r≦43) [ar/44]に一致する
端点を除いた斜辺上における格子点は(1≦x≦43)の範囲で直線y=ax/44に乗っている格子点(x,ax/44)であるが
ax/44が整数になることためにはxが44/gcd(a,44)の倍数でなければならない
1≦m×44/gcd(a,44)≦43となるmは1,2,…,(gcd(a,44)-1)なので、
結局、端点を除いた斜辺上にはgcd(a,44)-1個の格子点がある ところでm=(1+2+…+n)-1、δ(x)=1/2-x+[x]としたとき
Σ[1≦x≦n,1≦y≦m]δ(xy/m)=Σ[1≦x≦n]gcd(x,m)/2
とキレイに書けるけど何かいい説明あるんかな
>>990
はーなるほど
Σ[1≦r≦43] [ar/44] を直接計算するのは面倒でも、
格子点の個数と考えれば長方形の面積として簡単に計算できるんですね
ありがとうございます >>991
よく考えたら
Σ[1≦y≦m]δ(xy/m)=gcd(x,m)/2
が成り立ちますね
証明は先の長方形と対角線上の格子点を数える方法で出来る プログラムキチガイが無理矢理議論に参加しているのが笑える
早く死ねばいいのに
1辺の長さ1の正7角形の高さの厳密解を求めたら
こんな式になってしまった。もっと簡単にできるかもしれん。
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
>>996
あんたも手計算して参加すればいいのに。
wolfram使って確認する人もいるし
俺みたいに自作プログラムでカウントする人間もいる。
丸め誤差の処理しないバグがあったが。 lud20200824070957ca
このスレへの固定リンク: http://5chb.net/r/math/1595675377/ヒント:5chスレのurlに http://xxxx.5chb.net/xxxx のようにbを入れるだけでここでスレ保存、閲覧できます。TOPへ TOPへ
全掲示板一覧 この掲示板へ 人気スレ |
Youtube 動画
>50
>100
>200
>300
>500
>1000枚
新着画像
↓「高校数学の質問スレPart406 ->画像>32枚 」を見た人も見ています:
・高校数学の質問スレPart403
・高校数学の質問スレPart404
・高校数学の質問スレ Part412
・高校数学の質問スレ Part436
・高校数学の質問スレPart398
・高校数学の質問スレ Part421
・高校数学の質問スレ Part419
・高校数学の質問スレ Part417
・高校数学の質問スレ Part422
・高校数学の質問スレ Part423
・高校数学の質問スレ Part420
・高校数学の質問スレPart405
・高校数学の質問スレPart401
・高校数学の質問スレ Part413
・高校数学の質問スレ Part433
・高校数学の質問スレPart399
・高校数学の質問スレPart401
・高校数学の質問スレPart407
・高校数学の質問スレPart402
・高校数学の質問スレ Part416
・高校数学の質問スレPart409
・高校数学の質問スレ Part427
・高校数学の質問スレ Part438
・高校数学の質問スレ Part426
・高校数学の質問スレ Part430
・高校数学の質問スレ Part411
・高校数学の質問スレPart408
・高校数学の質問スレ Part429
・高校数学の質問スレ Part424
・高校数学の質問スレ Part438
・高校数学の質問スレ(医者・東大卒専用) Part438
・高校数学の質問スレ(医者・東大卒禁止) Part438
・高校数学の質問スレ(国立医・東大合格者専用) Part439 (40)
・大学数学の質問スレ Part1
・高校数学の間違いを指摘するスレ
・【sin】高校生のための数学の質問スレPART29【cos】
・面白い高校数学の問題貼ってくスレ (9)
・数学の質問です
・高校数学のベクトルは何なの?
・高校数学の「図形と方程式」とかいう名称
・ベクトルの外積って高校数学の教科書に載ってるんだね
・大学以上質問スレッド
・プロレベル質問スレ
・積分順序の問題についての質問スレ
・大学学部レベル質問スレ 27単位目
・大学学部レベル質問スレ 17単位目
・大学学部レベル質問スレ 24単位目
・大学学部レベル質問スレ 2単位目
・大学学部レベル質問スレ 9単位目
・大学学部レベル質問スレ 25単位目
・大学学部レベル質問スレ 19単位目
・大学学部レベル質問スレ 6単位目
・大学学部レベル質問スレ 13単位目
・大学学部レベル質問スレ 4単位目
・大学学部レベル質問スレ 23単位目
・大学学部レベル質問スレ 8単位目
・高校数学レベルの自作問題にチャレンジするスレ
・質問です
・線形代数の質問
・高校数学は暗記科目
・高校数学って要は
・三角形についての質問
・とある自然数だけど質問ある?































